


A matemática faz o indivíduo pensar, raciocinar e isto é muito bom para a mente.
Por exemplo, pegue o número 4 e divida por 2, vem na sua mente: 4 elementos, 4 objetos, etc., agora você divide por 2 (4:2=2); 2 elementos, 2 objetos, etc.
Você mentalmente faz grupos de quantos elementos têm, separando-os, para ver de que forma pode ser dividido, não deixa de ser uma operação simples e até banal para quem aprendeu a parte elementar da aritmética.
O número 4 fica fixado em sua mente e também o número 2, ai novamente você precisa fazer a mesma operação de divisão, 4 dividido por 2 dá 2, porque 4 divido por 2 tem como quociente o 2, esta é a lei, está é a regra, mas convenhamos, as regras vieram muito tempo depois, e essa capacidade é inerente do ser humano de poder pensar, analisar as coisas que nos rodeiam.
O que quero dizer é que o número 4 é um número fixo, uma quantidade fixa, você olha para ele e na sua mente você vê 4, associa a 4 coisas, a 4 objetos, a 4 elementos, etc.
Não dá para “esticar” o número 4 para que ele fique maior e quando for dividir por 2 dê sempre 2.
O que se pode fazer é pegar o dobro do dividendo 4 (o número 8), pegar o dobro do divisor 2 (o número 4) e efetuar a divisão novamente para que tenhamos um mesmo quociente (o número 2).
8 dividido por 4 é igual a 2.
Aliás, todo número par divido por 2, terá como resultado a metade desse número.
Agora, pense no número pi (3,1415925..), pense..., analise..., reflita...
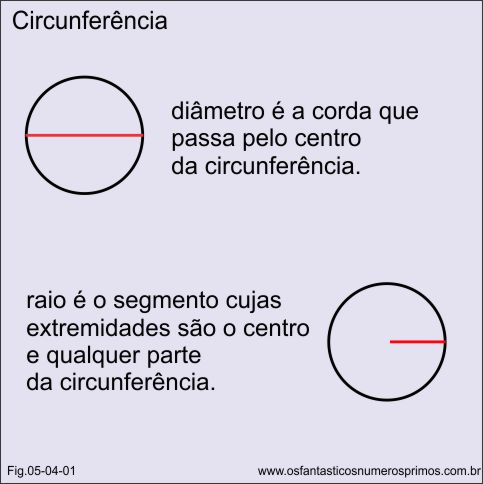
Um número que obtemos dividindo o comprimento de uma circunferência pelo seu diâmetro.
| CIRCUNFERÊNCIA | : | DIÂMETRO | = | Pi (Π) |
| CIRCUNFERÊNCIA | : | 2 x raio | = | Pi (Π) |
Ou fazendo a operação inversa:
| DIÂMETRO | x | Pi (Π) | = | CIRCUNFERÊNCIA |
| 2 | x | raio | x | Pi (Π) | = | CIRCUNFERÊNCIA |
Qualquer que seja o comprimento da circunferência, dividindo pela medida do seu diâmetro terá como resultado sempre um número pouco maior que 3 (3,1415925...).
Olhe que estamos falando de qualquer comprimento de circunferência, não existe um comprimento fixo. O comprimento pode ser pequeno, médio, grande, etc, um comprimento qualquer, e isso que é muito interessante, isso é que é o encanto da matemática, como se acontecesse num passe de mágica.
Como exemplos, tem-se na tabela abaixo a coluna diâmetro que multiplicados por (Pi) têm como produtos comprimentos de circunferências próximos a números inteiros.
| Diâmetro | PI | Circunferência | |
| 1,28 | x | 3,1415 | 4,02112 |
| 1,61 | x | 3,1415 | 5,057815 |
| 1,91 | x | 3,1415 | 6,000265 |
| 2,23 | x | 3,1415 | 7,005545 |
| 2,55 | x | 3,1415 | 8,010825 |
| 2,87 | x | 3,1415 | 9,016105 |
| 3,19 | x | 3,1415 | 10,021385 |
| 3,51 | x | 3,1415 | 11,026665 |
| 3,85 | x | 3,1415 | 12,094775 |
| 4,15 | x | 3,1415 | 13,037225 |
| 4,46 | x | 3,1415 | 14,01109 |
| 4,78 | x | 3,1415 | 15,01637 |
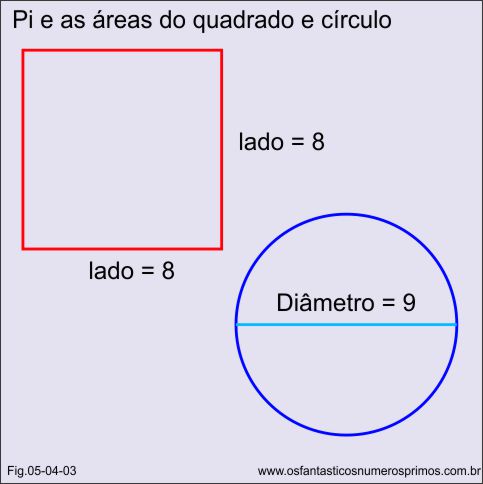
No Papiro de Rhind há o prolema de número 50 em que os egípcios determinam a área de um circulo com a fração 256/81 = 3,16049, resultado próximo a pi (Π), relacionando a área de um círculo de diâmetro 9 e um quadrado de lado 8.
Estudos presumem que eles chegaram a este resultado inscrevendo um octógono em quadrado.
A área do círculo é bem próxima ao do octógono inscrito em um quadrado de lado D.
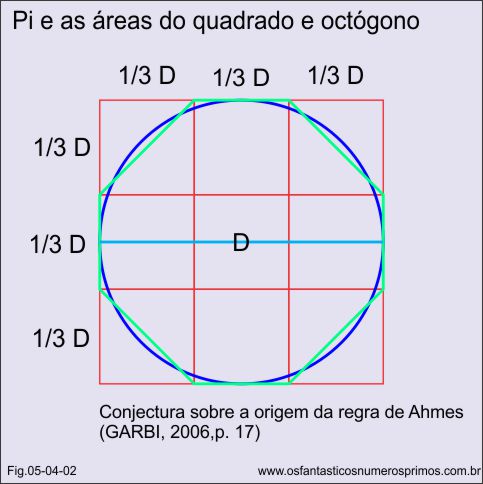
Área do octógono:
| 7 | |
| ____ | D2 |
| 9 |
| 7 x 9 | |
| ____ | D2 |
| 9 x 9 |
| 63 | |
| ____ | D2 |
| 81 |
Valor aproximado:
| 64 | |
| ____ | D2 |
| 81 |
| 8 | |
| ____ | D2 |
| 9 |
Fazendo a equivalências das áreas chega-se a um valor aproximado de Pi.
| 92 | |||
| Π | ____ | = | 8 x 8 |
| 22 |
| 81 | |||
| Π | ____ | = | 64 |
| 4 |
| Π | 81 | = | 64 x 4 |
| 256 | ||
| Π | = | ________ |
| 81 |
| 256 | ||
| Π | = | ________ |
| 81 |
| 13 | ||
| Π | = | 3 x ________ |
| 81 |
| Π | = | 3, 16 |
No documentário The Story of Maths - The Language of The Universe, produzido pela Open Unisersity e pela BBC, ano 2007, o Prof. Marcus Du Sautoy conjectura que a aproximação do número Pi realizado pelo egípcios tenha sido originado do Jogo Mancala.
No tabuleiro do Jogo Mancala há trilhas de sulcos cônvavos em formatos de meia esfera, nas quais vão se colocando pedrinhas arredondadas, semelhantes bolinhas de gude, formando figuras de círculos.
O Prof. Marcus, então, esparrama 64 pedrinhas no chão e vai moldando-as formando a figura de círculo cujo o diâmetro aparece 9 pedrinhas enfileiradas, concluindo o seguinte raciocínio:
Quadrado de 8
8 x 8 = 64
metade de 9 ao quadrado
9 : 2 = 4,5
4,52 = 20,25
Quadrado de 8 dividido pela metade de 9 ao quadrado
64 : 20,25 = 3,16
The math makes one think, reason , and sometimes he does not realize it , because it is ingrained in our minds . For example, take the number 4 and divide by 2 , comes to your mind : 4 elements , 4 objects , etc. , now you divide by 2 ( 4:2 = 2 ) 2 elements , 2 objects , etc. . .
You mentally groups does have many elements , separate them , to see how it can be divided , it is still a simple, even banal to those who have learned the elementary part of the arithmetic operation .
The number 4 is fixed in your mind and also the number 2 , there again you need to do the same operation , division 4 divided by 2 gives 2 because 4 divided by 2 is 2 as the quotient , this is the law , it is the rule , but face it, the rules came much later, and this capability is inherent in the human being to be able to think, analyze things that surround us .
What I mean is that the number 4 is a fixed number , a fixed amount , and you look at it in your mind you see 4 associates the 4 things, objects 4 , the 4 elements , etc. .
You can not " stretch " the number 4 for it to get bigger and when you divide by 2 always give 2 .
What you can do is get the double dividend of 4 ( number 8 ) , take twice the divisor 2 (number 4 ) and make the division again so that we have the same quotient ( number 2 ) . 8 divided by 4 equals 2.
Now , think of the number pi ( 3.1415925 .. ) , think ...
We obtain a number by dividing the length of a circumference by its diameter .
| CIRCUNFERÊNCIA | : | DIÂMETRO | = | Pi |
Or making inverva operation:
| DIÂMETRO | x | Pi | = | CIRCUNFERÊNCIA |
Whatever the length of the circumference divided by the measure of its diameter will result when the bit number greater than 3 (3.1415925 ...)
Look we're talking about the circumference of any length, there is no fixed length.
The length can be small, medium, large, etc., of any length, and it is very interesting, is that this is the charm of mathematics, as if it happened by magic.
Examples are in Table diameters multiplied by (pi) have lengths as a result of the circumferences near integers.
La matemática hace pensar , razonar, ya veces no se da cuenta , porque está arraigado en nuestras mentes. Por ejemplo , tome el número 4 y se divide por 2, que viene a su mente : 4 elementos, 4 objetos, etc , ahora se divide por 2 ( 04:02 ) = 2 2 2 elementos, objetos, etc ..
Usted mentalmente grupos sí que tiene muchos elementos , separarlos , para ver la forma en que se puede dividir , todavía es un simple, incluso banal para aquellos que han aprendido la parte elemental de la operación aritmética .
El número 4 se fija en su mente y también el número 2 , allí de nuevo que tiene que hacer la misma operación , la división 4 dividido entre 2 da 2 ya 4 dividido por 2 es 2 como el cociente , esto es la ley , es la regla, pero la cara él, las reglas llegaron mucho más tarde, y esta capacidad es inherente al ser humano a ser capaz de pensar , analizar las cosas que nos rodean
Lo que quiero decir es que el número 4 es un número fijo , una cantidad fija, y nos fijamos en que en su mente se ve 4 asociados las 4 cosas , objetos 4 , los 4 elementos , etc .
Usted no puede " estirar" el número 4 a que se haga más grande y cuando se divide por 2 siempre dan 2 .
Lo que puedes hacer es conseguir el doble dividendo de 4 (número 8 ), tomar dos veces el divisor 2 (número 4 ) y hacer la división de nuevo, así que tenemos el mismo cociente ( número 2 ) . 8 dividido por 4 es igual a 2 . Ahora , piense en el número pi (3.1415925 ..) , piensa ...
Se obtiene un número dividiendo la longitud de una circunferencia por su diámetro.
| CIRCUNFERÊNCIA | : | DIÂMETRO | = | Pi |
O haciendo la operación inverva:
| DIÂMETRO | x | Pi | = | CIRCUNFERÊNCIA |
Cualquiera que sea dará como resultado la longitud de la circunferencia dividida por la medida de su diámetro cuando el número de bits mayor que 3 (3.1415925 ... )
Mira que estamos hablando de la circunferencia de cualquier longitud, no existe una longitud fija. La longitud puede ser pequeña , mediana, grande , etc , de cualquier longitud , y es muy interesante , es que este es el encanto de las matemáticas , como si hubiera ocurrido por arte de magia .
Ejemplos son en diámetros Tabla multiplicado por ( PI ) tienen longitudes como resultado de las circunferencias cerca de números enteros .
Autor: Ricardo Silva
NAKAMURA, Keiji. Conjunto do números irracionais: a trajetória de um conteúdo não incorporado às práticas educacionais. Dissertação de Mestrado. Pontifícia Universidade Católica. São Paulo, 2008
SAUTOY, Marcus Du . The Story of Maths - The Language of The Universe, produzido pela Open Unisersity e pela BBC, 2007
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato