Página de estudos de matemática e sequências numéricas

Números quadrados perfeitos: suas raízes, seus intervalos e suas diferenças - parte 1- 040

Números quadrados perfeitos são obtidos multiplicando-se um número inteiro por ele mesmo e consequentemente a sua raiz quadradra também é um número inteiro.

Analisando os números quadrados perfeitos, outras informações consegue-se extrair de sua sequência que nos mostram detalhes de como se interligam com suas raízes quadradas, intervalos e diferenças entre dois números quadrados.

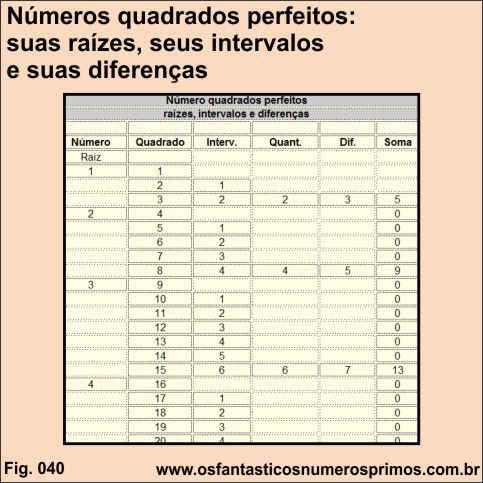
Os intervalos entre números quadrados perfeitos apresentam sequência de números pares e a diferença entre quadrados apresentam números ímpares.

Coluna Quadrado

Apresenta a sequência de números naturais a partir de 1, na qual foram destacados na cor amarelo números que são quadrados perfeitos. Entre dois quadrados, há números que não são quadrados perfeitos.

Exemplos:

a) o número 2 não é um quadrado perfeito.

b) o número 3 não é um quadrado perfeito.

c) o número 5 não é um quadrado perfeito.

A partir do número 1 podemos obter um quadrado perfeito, multiplicando um número por ele mesmo, mas nem todo o número é um quadrado perfeito.

Coluna Número / Raiz

Apresenta a sequência de números a partir de 1 em ordem crescente. Aqui podemos observar que a própria sequência é tambem a raiz dos números da coluna QUADRADO.

Coluna Intervalo

Aqui já podemos ver outra sequência proveniente dos intervalos entre dois números quadrados pefeitos: a sequência de números pares (2, 4, 8, 10, 12, 14, 16, 18,...).

Exemplos:

 a) entre os quadrados 1 e 4, há 2 intervalos com os números 2 e 3 em cada intervalo. Os números 2 e 3 não são números quadrados perfeitos.

b) entre os quadrados 4 e 9, há 4 intervalos com os números 5, 6, 7, e 8 em cada intervalo. Os números 5, 6. 7 e 8 não são números quadrados perfeitos.

c) Entre os quadrados 9 e 16, há 6 intervalos com os números 10, 11, 12, 13, 14 e 15. Os números 10, 11, 12, 13, 14 e 15 não são quadrados perfeitos.

Coluna Quantidade

Aqui de uma forma sintética, apresenta a quantidade de números entre os intervalos dos números quadrados perfeitos.

Coluna Diferença

Apresenta a diferença ente dois números quadrados perfeitos.

A diferença entre dois quadros é um número ímpar.

Exemplos:

 a) o quadrado 1 subtraído do quadrado 4

4 - 1 = 3

b) quadrado 4 subtraído do quadrado 9

9 - 4 = 5

c) o quadrado 9 subtraído do quadrado 16

16 -9 = 7

Observação: Enquanto os intervalos entre os quadrados são número pares, as diferenças são números ímpares.

A partir desta constatação foram somados um número referente ao intervalo e um número referente a diferença entre dois números quadrados.

Coluna Soma

Apresenta a soma da quantidade de números entre os intervalos com a diferença entre dois números quadrados perfeitos.

A partir de 5 somando-se 4 unidades, obtem-se a seguinte sequência: 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49, 53, ..., entre eles ocorrências de números primos: 5, 13, 17, 29, 41, 53, ...

Exemplo a)

A soma da quantidade 2 mais a diferença 3 é igual a 5.

2 + 3 = 5

Observação: 5 é um número primo.

Exemplo b)

A soma da quantidade 4 mais a diferença 5 é igual a 9.

4 + 5=9

Observação: 9 é um número quadrado perfeito.

Tabela 1 - Números quadrados perfeitos

Tabela 2 - Números quadrados perfeitos

Tabela 3 - Números quadrados perfeitos

Autor: Ricardo Silva

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-153-numeros-quadrados-raizes-intervalos-diferencas-parte-2

Livro digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.