


Se te perguntassem qual é a soma dos ângulos internos de um triângulo, certamente, você diria como resposta 180 graus, o que seria a resposta da maioria da pessoas.
Se te perguntassem qual é a soma dos ângulos internos de um triângulo numa superfície plana, isto é, em uma superfície de curvatura zero e você respondesse 180 graus, infelizmente a sua resposta não estaria totalmente correta.
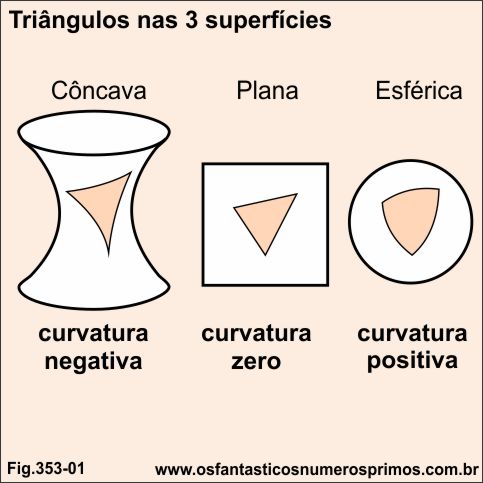
Fonte: A magia dos números no universo
Dependendo da superfície em que um triângulo é desenhado, a soma dos seus ângulos internos sofrem variações:
a) em superfície de curvatura negativa, a soma dos ângulos internos de um triângulo é menor que 180 graus;
b) em supefície de curvatura positiva, a soma dos ângulos internos de um triângulo é maior que 180 graus;
c) em supefície de curvatura zero, isto é, num plano, a soma dos ângulos internos de um triângulo também apresentam variação para menor ou maior que 180 graus;
Neste estudo são apresentados casos particulares em que são possíveis de construírem triângulos num plano cuja soma dos seus ângulos internos são menores, iguais ou maiores que 180 graus.
Por muito tempo os conhecimentos matemáticos e geométricos foram utilizados de maneira prática, por meio de erros e acertos e experimentações até que se encontrasse a devida solução. O aprendizado se dava de forma empírica observando os padrões que se repetiam.
Na antiga Grécia, em seus tempos áureos, muitos foram os homens que se dedicaram aos estudos de vários ramos das ciências, como a matemática e a geometria e que deixaram um grande legado de conhecimentos nas resoluções de problemas relacionados a cálculos de áreas, construções de figuras geométricas bem como sólidos geométricos, aritmética, etc.
Em se tratando de geometria, três são os problemas geométricos que os gregos tentaram resolvê-los com a utilização apenas de régua não graduada e compasso:
Duplicação do Cubo - Construir um cubo que tem o dobro do volume de outro cubo;
Quadratura do Círculo- Construir um quadrado que tenha área igual a de um círculo;
Trissecção do ângulo - Dividir um ângulo em três partes iguais...
...e que perduram até os dias atuais.
Pode-se dividir qualquer ângulo em duas partes iguais, mas em se tratando de dividí-lo em 3 partes iguais a tarefa não é tão simples assim, que o digam os grandes mestres como Hípias de Elis, Arquimedes, Nicômedes que tentaram solucionar tal problema.
Podemos perfeitamente dividir um um ângulo de 90 graus em 3 partes iguais fazendo o uso exclusivamente de régua não graduada e compasso.
Veja materias relacionadas
No Wikipédia e no livro Construções Geométricas - Volume 1 - Módulo 1 - 2ª edição - página 69 - autor: Cláudio Santos de Souza, são apresentados a seguinte construção geométrica para trissecção de ângulo por método aproximado e também um estudo algébrico do mesmo.
Tanto no Wikipédia quanto no livro Construções Geométricas e algumas dissertações de mestrados consultadas não apresentam o nome do autor da Trissecção de Ângulo - Método Aproximado.
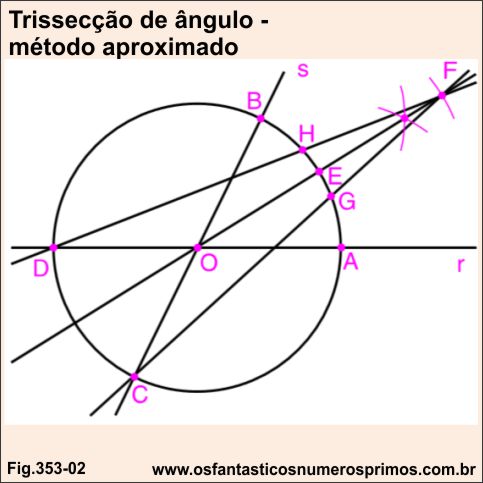
A trissecção do ângulo de 90 graus realizada pelo Método Aproximado, obtêm-se os seguintes ângulos: 29,3, 31,4 e 29,4 graus.
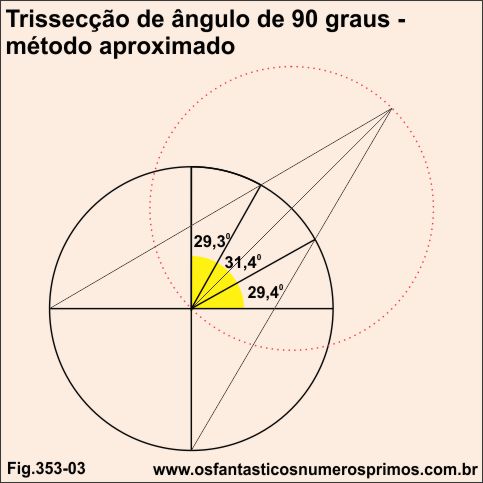
Unindo-se o centro da circunferência às intersecções das trissecções obtem-se 3 triângulos cujas soma dos ângulos internos são menores e maiores que 180 graus.
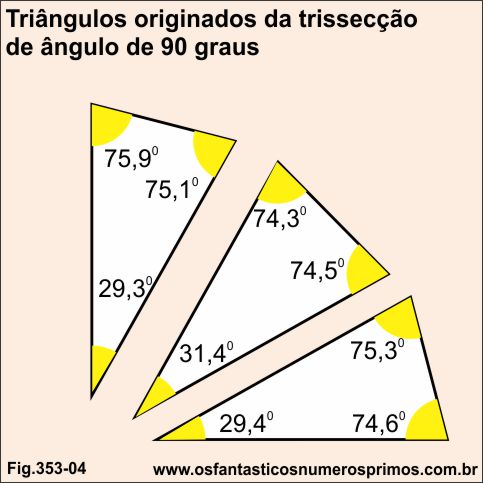
| Trissecção de ângulo de 90 graus | |||
|---|---|---|---|
| ângulos internos | ângulos internos | ||
| reais | arredondados | ||
| Triângulo 1 | |||
| 75,3 | 75 | ||
| 74,6 | 75 | ||
| 29,4 | 29 | ||
| soma | 179,3 | 179 | |
| Triângulo 2 | |||
| 74,5 | 75 | ||
| 74,3 | 74 | ||
| 31,4 | 31 | ||
| soma | 180,2 | 180 | |
| Triângulo 3 | |||
| 75,9 | 76 | ||
| 75,1 | 75 | ||
| 29,3 | 29 | ||
| soma | 180,3 | 180 | |
| www.osfantasticosnumerosprimos.com.br | |||
A trissecção do ângulo de 60 graus realizada pelo Método Aproximado, obtem-se os seguintes ângulos: 19,7, 20,4 e 19,8 graus.
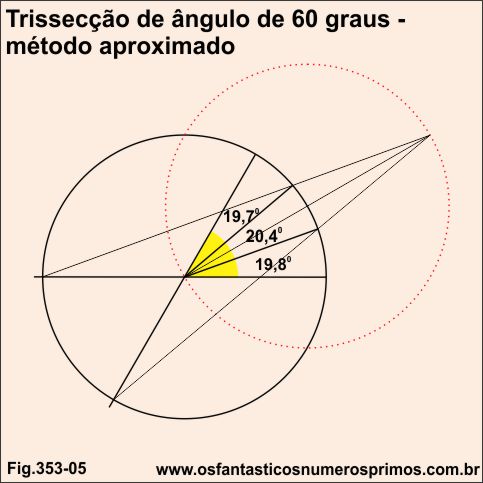
Unindo-se o centro da circunferência às intersecções das trissecções obtem-se 3 triângulos cujas soma dos ângulos internos são menor e iguais que 180 graus.
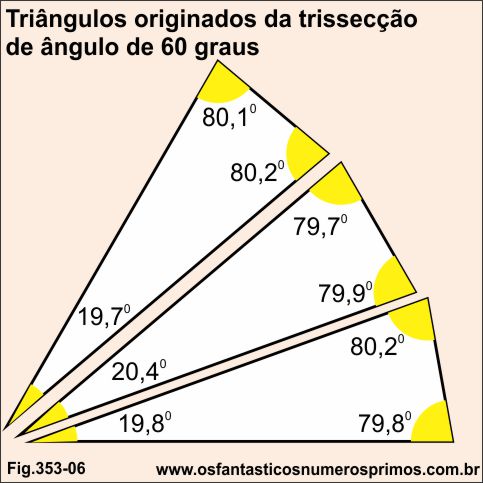
| Trissecção de ângulo de 60 graus | |||
|---|---|---|---|
| ângulos internos | ângulos internos | ||
| reais | arredondados | ||
| Triângulo 1 | |||
| 80,1 | 80 | ||
| 80,2 | 80 | ||
| 19,7 | 20 | ||
| soma | 180 | 180 | |
| Triângulo 2 | |||
| 79,7 | 80 | ||
| 79,9 | 80 | ||
| 20,4 | 20 | ||
| soma | 180 | 180 | |
| Triângulo 3 | |||
| 80,2 | 80 | ||
| 79,8 | 80 | ||
| 19,8 | 20 | ||
| soma | 179,8 | 180 | |
| www.osfantasticosnumerosprimos.com.br | |||
A trissecção do ângulo de 45 graus realizada pelo Método Aproximado, obtem-se os seguintes ângulos: 15, 15 e 14,9 graus.
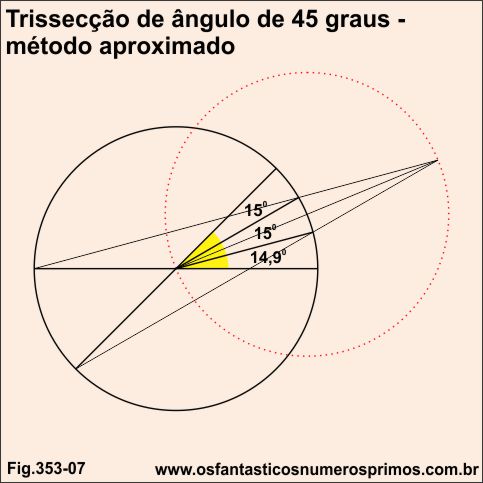
Unindo-se o centro da circunferência às intersecções das trissecções obtem-se 3 triângulos cujas soma dos ângulos internos são menor e maior que 180 graus.
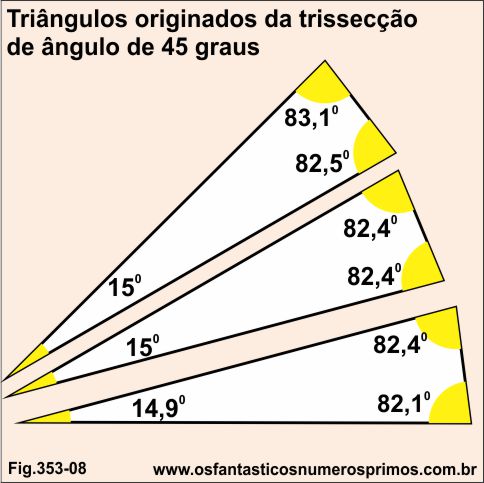
| Trissecção de ângulo de 45 graus | |||
|---|---|---|---|
| ângulos internos | ângulos internos | ||
| reais | arredondados | ||
| Triângulo 1 | |||
| 83,1 | 83 | ||
| 82,5 | 83 | ||
| 15 | 15 | ||
| soma | 180,6 | 181 | |
| Triângulo 2 | |||
| 82,4 | 82 | ||
| 82,4 | 82 | ||
| 15 | 15 | ||
| soma | 179,8 | 179 | |
| Triângulo 3 | |||
| 82,4 | 82 | ||
| 82,1 | 82 | ||
| 14,9 | 15 | ||
| soma | 179,4 | 179 | |
| www.osfantasticosnumerosprimos.com.br | |||
Autor: Ricardo Silva - novembro/2021
OSSERMAN, Robert, A mágia dos números no universo; tradução: Júlia Bárány. São Paulo: Mercúryo, 1997
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
SOUZA, Cláudio Santos de. Construções geométricas. v.1 / Cláudio Santos de Souza. – 2.ed. – Rio de Janeiro : Fundação CECIERJ, 2005. 196 p.; 21 x 29,7 cm.

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato