


Circunferência é uma figura geométrica ímpar, pois apresenta diversas propriedades aritméticas, algébricas, geométricas e trigonométricas com ela própria e com as demais figuras geométricas.
A partir dela pode-se construir infinitos polígonos regulares inscritos e circunscritos.
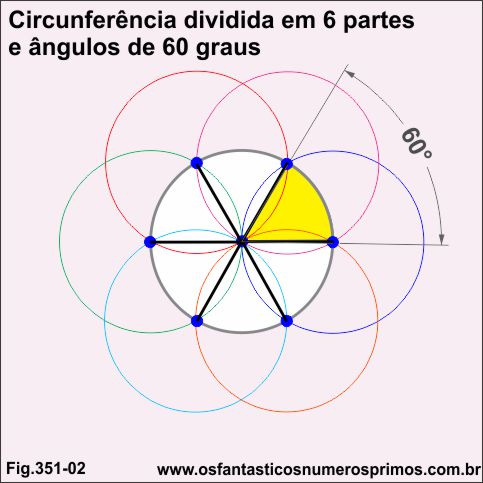
Outra propriedade que podemos destacar é quando dividimos uma circunferência em 6 partes.
Qualquer que seja a medida do raio ou diâmetro e marcamos um ponto aleatório sobre uma circunferência central e desenharmos mais 6 réplicas de mesmo raio de forma que o centro de cada réplica fique na intersecção com a circunferência central e a circunferência anterior, determinan-se 6 divisões de 60 graus cada uma.

Traçando-se seguimentos a partir de pontos diametralmente opostos, obtêm-se ângulos de 60 graus e que somados consecutivamente têm-se 120, 180, 240, 300, 360, todos ângulos múltiplos de 60 graus.
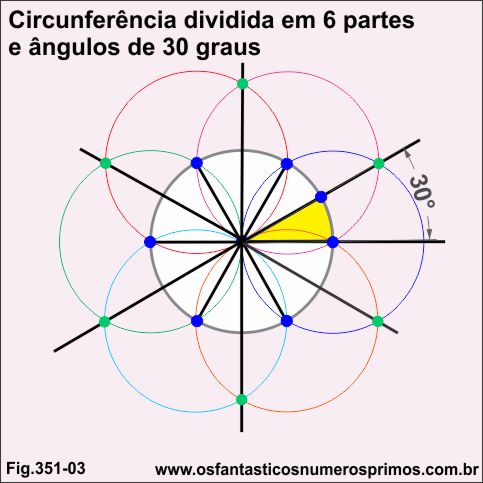
Traçando-se seguimentos do centro da circunferência principal até as intersecções de duas circunferências (ponto verde) à parte externa da circunferência principal, obtêm-se ângulos de 30 graus.
O ângulo de 30 graus corresponde a divisão de uma circunferência em 12 partes.
Somados consecutivamente ângulos de 30 graus, têm-se 60, 90, 120, 150, 180, 210, 240, 270, 300, 330 e 360 todos ângulos múltiplos de 30 graus.
Desenhando-se outra circunferência (laranja) cujo centro esteja no ponto de ângulo de 30 graus e traçarmos um segmento do centro da circunferência central até a intesecção de duas circunferências (ponto azul), determina-se assim um ângulo de 15 graus.
O ângulo de 15 graus corresponde a divisão de uma circunferência em 24 partes.

Aproveitando as etapas anteriores de construção de ângulo de 15 graus, traça um segmento do centro da circunferência principal até intersecção de duas circunferências (ponto amarelo), determinando um ângulo de 45 graus.
O ângulo de 45 graus corresponde a divisão de uma circunferência em 8 partes.

Traçando um segmento vertical do centro da circunferência até a intersecção de duas circunferência (ponto lilás) na parte exterior e outro segmento horizontal determina-se um ângulo de 90 graus.
O ângulo de 90 graus corresponde a divisão de uma circunferência em 4 partes.

Autor: Ricardo Silva - outubro/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato