


Pesquisando e estudando tópicos sobre relações métricas no triângulo retângulo e na circunferência em livros, teses de mestrados, ensaios, apostilas, vídeo-aulas bem como em WebSites, notei que diversos são os exemplos e exercicíos que procuram demonstrar como encontrar medidas de raios, diâmetros ou lados de triângulos retângulos inscritos ou circunscritos em circunferências ou circunferências inscritas ou circunscritas em triângulos.
Os exemplos e exercícios em questão fazem demonstrações com triângulos retângulos pitagóricos "prontos", isto é, tem-se um triângulo inscrito ou circunscrito em circunferência ou circunferência inscrita ou circunscrita em um triângulo.
Até o presente momento não se encontrou um só tópico que discorresse de como alinhar circunferência em um plano e posteriormente inscrever ou circunscrever polígonos, sejam regulares ou irregulares com instrumentos: régua e compasso.
Neste estudo são apresentados métodos usuais auxiliares de como alinhar circunferência em um plano, isto é, fazer com que o diâmetro fique paralelo ao plano e acredito ser um tópico que possa ser acrescentado a Geometria e assim ser também estudado por profissionais e professoes da área de exatas, bem como, por estudantes e entusiastas matemáticos, etc...
Executando-se desenho de circunferência com o uso somente de régua e compasso numa folha de papel, por exemplo, formato A4, cujas medidas são 210 mm x 297 mm, podemos utilizar métodos geométricos clássicos para centralizar desenhos:
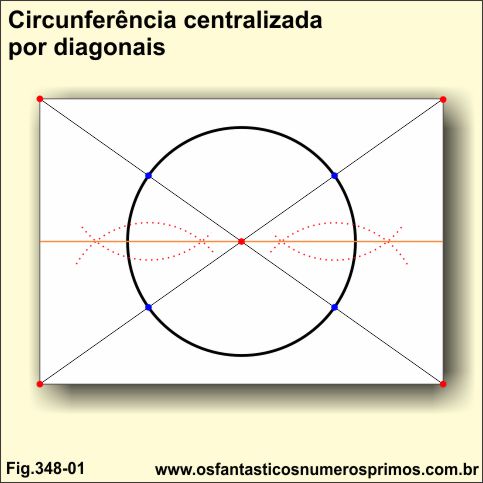
a) traça-se duas linhas diagonais e na intersecção destas, coloca-se a ponta seca do compasso e desenha-se a circunferência;
b) as diagonais formam retas concorrentes obliquas, isto porque a base é retangular;
c) traçando-se as bissetrizes dos ângulos agudos, linha laranja, obtem-se o diâmetro e consequentemente a circunferência pararela ao plano.
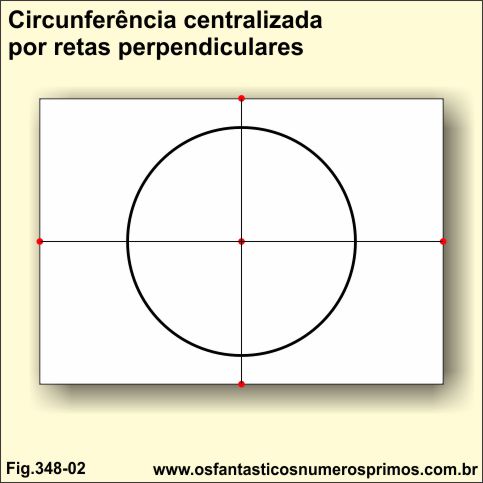
d) traça-se duas retas perpendiculares a partir do ponto médio de cada lateral da folha de papel e na intersecção destas, coloca-se a ponta seca do compasso e desenha-se a circunferência, desta forma, o diâmetro também fica paralelo ao plano.
e) sendo o suporte de desenho em formato quadrado, traça-se duas retas perpendiculares "inclinadas" e as bissetrizes horizontais, obtendo se assim o seguimento laranja e consequentemente o diâmetro paralelo ao plano.

O método de desenho de circunferência com uso de retas perpendiculares auxiliares conforme Fig. 348-02 apresenta-se bastante vantajoso, pois automaticamente, a circunferência passa a ser dividida em duas semi-circunferências, isto é, em duas partes de 180 graus e também em 4 partes de 90 graus cada uma.
A partir das intersecções entre as retas perpendiculares e a circunferência, ao traçarmos bissetrizes, podemos fazer sucessivas divisões cujas partes são potências de base 2: 2, 4, 8, 16, 32, 64,...
Outro aspecto muito importante dessa construção com auxílio de retas perpendiculares é que qualquer figura que façamos, seja ela inscrita ou circunscrita numa circunferência, ela estará alinhada horizontal e verticalmente ao suporte que está sendo desenhado, neste exemplo, a folha de papel.
Polígonos regulares de lados pares inscritos e circunscritos em circunfêrencias apresentam um padrão em suas construções geométricas: dois dos vértices dos polígonos se alinham a linha perpendicular vertical.
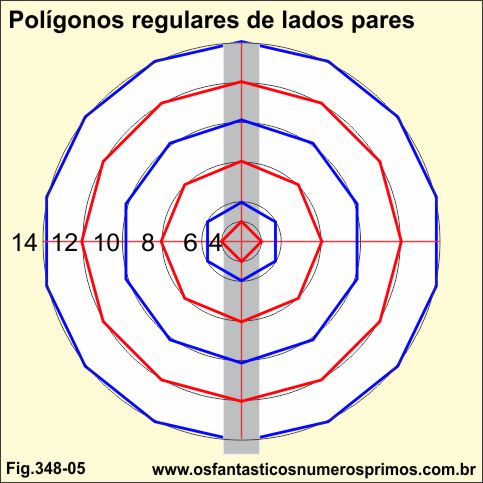
Polígonos regulares de lados ímpares inscritos ou circunscritos em circunfêrencias apresentam um padrão em suas construções geométricas: os lados que formam as base ficam alinhados na parte inferior a linha perpendicular vertical enquanto um dos vértices alinhados à parte superior.
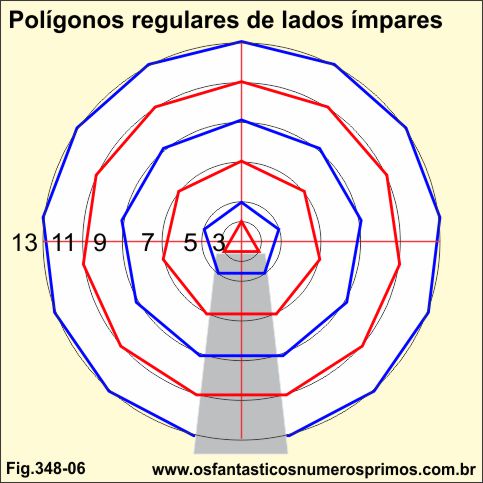
Com o uso de retas perpendiculares, pode-se dividir a circunferência em partes cujas quantidades são múltiplos de 3: 3, 6, 12, 24, 48,... e assim sucessivamente.
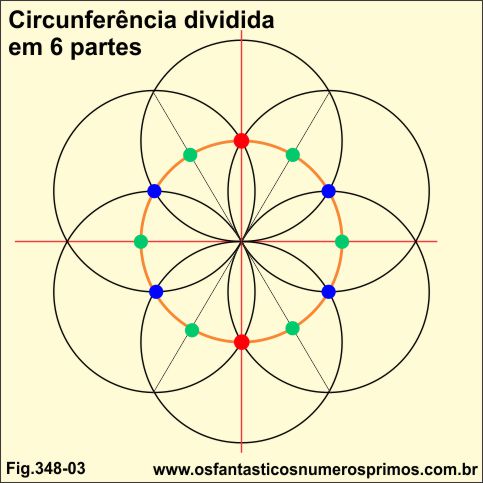
No exemplo, circunferência dividida em 6 partes e que se seguiu as seguintes etapas:
a) na intersecção com a circunferência (laranja) e a linha vertical, marcou-se os pontos em (vermelho);
b) desenhou-se circunferências com centro nos pontos (vermelho) de mesmo diâmetro da circunferência (laranja);
c) nas intersecções das circunferências com a circunferência (laranja) marcou-se os pontos em (azul);
d) a partir dos pontos em (azul), desenhou-se novas circunferências.
Podemos continuar o processo, marcar novas bissetrizes e nas intersecções dos pontos em (verde) desenhar também novas circunferências, bem como obter novas divisões e ângulos.
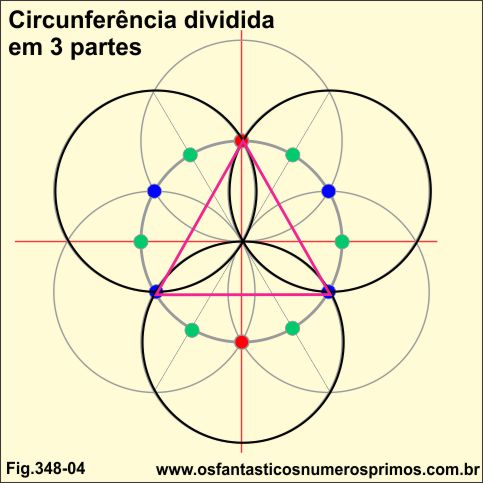
No exemplo, circunferência dividida em 3 partes com triângulo equilátero inscrito na cor (magenta), construída a partir da circunferência dividida em 6 partes.
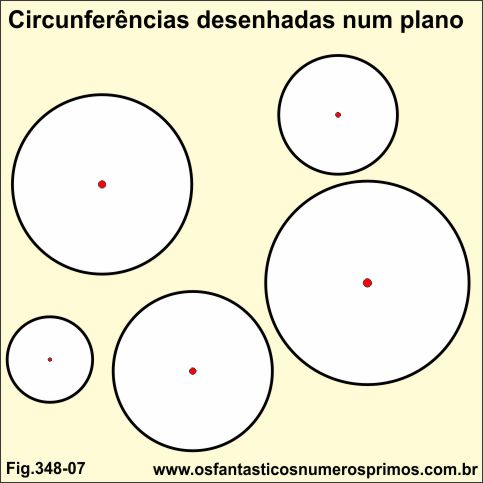
Podemos desenhar circunferências de variados comprimentos de raios ou diâmetros utilizando:
a) compasso;
b) objetos circulares como tampas, discos, etc. e os contornando;
c) linhas, barbantes ou cordas cujas pontas tenham objetos amarrados e que possar servir para riscar ou demarcar a própria circunferência.
O questionamento que se faz, é o seguinte: como fazer o diâmetro de uma circunferência ficar alinhado horizontal ou verticalmente ao plano a partir da própria circunferência?
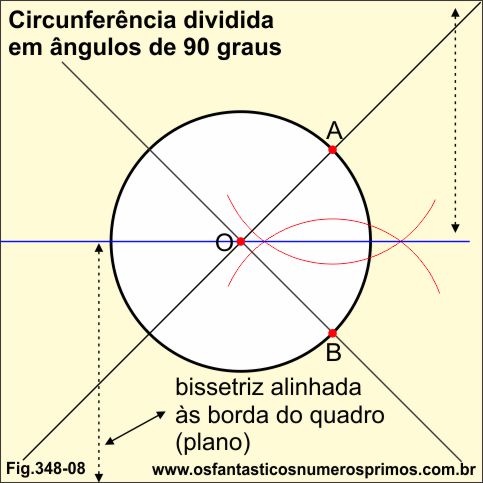
Seja uma circunferência traçada na intersecção de duas retas perpendiculares formando um "xis", neste caso, um suporte em formato quadrado.
Traçando-se a bissetriz do ângulo AÔB, alinhamos a circunferência ao plano, isto é, o seguimento de reta que está dividindo o ângulo AÔB em duas partes iguais está paralelo às linhas horizontal superior e inferior do plano.
Etapa 1)
Seja uma circunferência de raio ou diâmetro qualquer.
Marcam-se 3 pontos aleatórios sobre a circunferência e posteriormente traçamos as mediatrizes r e s dos seguimentos AB e BC.
Na intersecção das duas mediatrizes, o ponto O, é centro da circunferência.
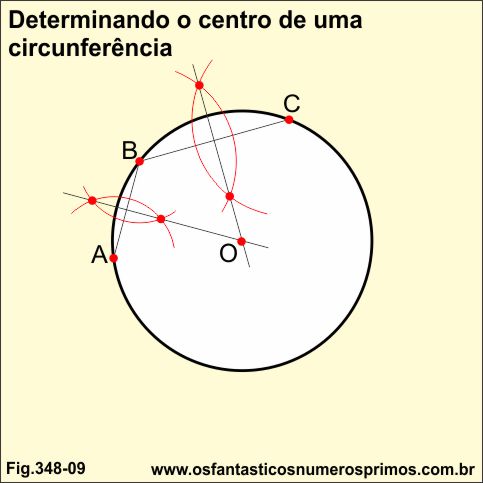
Etapa 2)
Prolonga-se o seguimento s até a circunferência, formando se assim o diâmetro.
Traça-se a mediatriz t do seguimento DE e posteriormente os pontos FG, formando-se assim as retas perpendiculares.
A circunferência fica dividida em 4 partes de 90 graus.
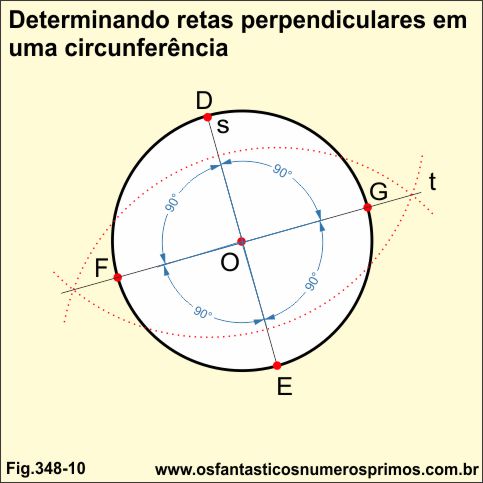
1a divisão
Traça-se a bissetriz u do ângulo EG.
O ângulo EG de 90 graus fica dividido em 2 ângulos de 45 graus.
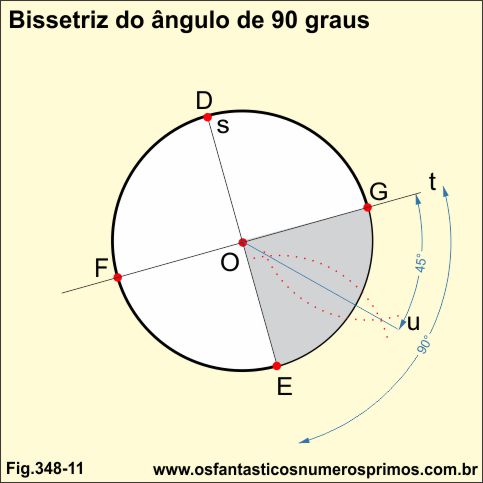
2a divisão
Traça-se a bissetriz v do seguimento GH.
O ângulo EG de 45 graus fica dividido em 2 ângulos de 22,5 graus.
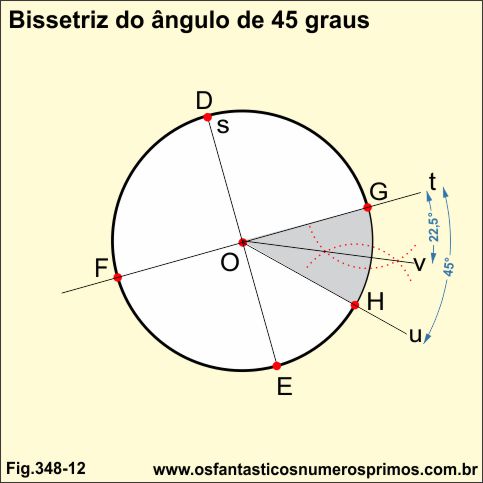
3a divisão
Traça-se a bissetriz x do seguimento GI.
O ângulo GI de 22,5 graus fica dividido em 2 ângulos de 11,25 graus.
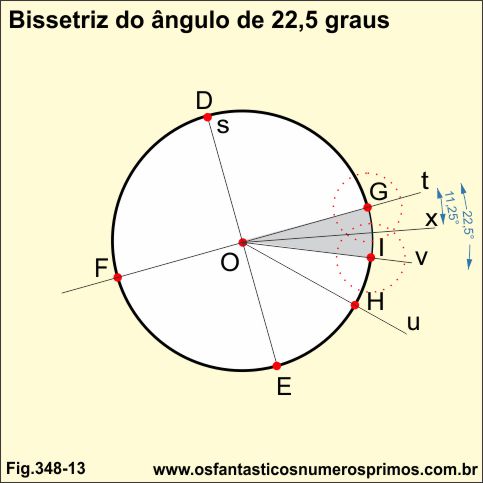
4a divisão
Traça-se a bissetriz y do seguimento IJ.
O ângulo GI de 11,25 graus fica dividido em 2 ângulos de 5,625 graus.
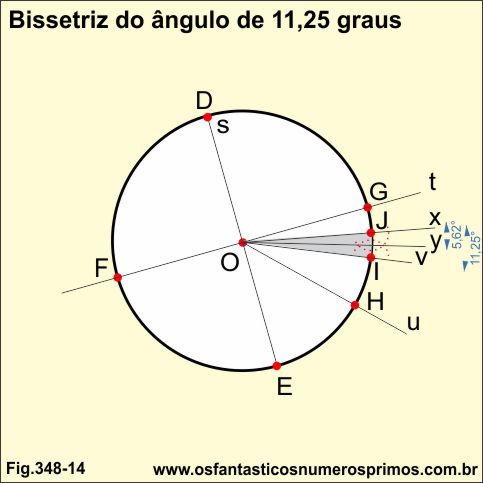
5a divisão
Traça-se a bissetriz z do seguimento JK.
O ângulo JK de 5,625 graus fica dividido em 2 ângulos de 2,8125 graus.
Nesta divisão, a mediatriz z se encontra perto do seguimento de reta de cor (azul) que passa pelo centro da circuferência.
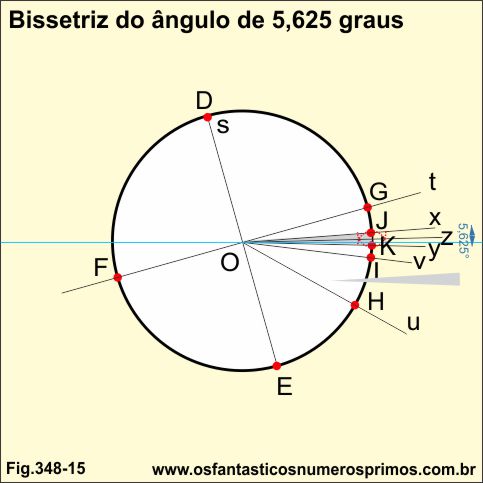
Continuando as divisões dos ângulos seguintes:
6a divisão
2,8125 : 2 = 1,40625 graus.
7a divisão
1,40625 : 2 = 0,703125 graus.
8a divisão
0,703125 : 2 = 0,3515625 graus (aproximadamente 1/2 grau)
9a divisão
0,3515625 : 2 = 0,17578125 graus.
10a divisão
0,17578125 : 2 = 0,087890625 graus.
Será que encontraremos a medida de 0 grau absoluto na circunferência?
Como podemos perceber, o alinhamento do diâmetro da circunferência num plano são aproximações e não 0 (zero) absoluto.
Outro questionamento que se faz é: quando três pontos marcados aleatoriamente numa circunferência e seguindo estas etapas de divisões sucessivas de um ângulo, conseguir-se-á alinhar o diâmetro de uma circunferência num plano com régua e compasso.
O número 360 é um número composto e seus divisores são:
D(360): {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360)
Dividindo-se 360 pelos divisores: 2, 3, 5, 9 e 15 e alguns múltiplos desses divisores, em determinado momento o quociente tem como resultado um número decimal, não sendo possível ter resultado de 0 (zero) grau nas sucessivas divisões.
Divisão de circunferência em múltiplos de 2.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por partes (potências) | |||||
| de base 2 | |||||
| Partes | |||||
| 360 | : | 2 | = | 180 | graus |
| 360 | : | 4 | = | 90 | graus |
| 360 | : | 8 | = | 45 | graus |
| 360 | : | 16 | = | 22,5 | graus |
| 32 | 11,25 | ||||
| 64 | 5,625 | ||||
| 128 | 2,8125 | ||||
| www.osfantasticosnumerosprimos.com.br | |||||
Divisão de circunferência em múltiplos de 3.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 3 | |||||
| Partes | |||||
| 360 | : | 3 | = | 120 | graus |
| 360 | : | 6 | = | 60 | graus |
| 360 | : | 12 | = | 30 | graus |
| 360 | : | 24 | = | 15 | graus |
| 360 | : | 48 | = | 7,5 | graus |
| 96 | 3,75 | ||||
| 192 | 1,875 | ||||
| 384 | 0,9375 | ||||
| www.osfantasticosnumerosprimos.com.br | |||||
Divisão de circunferência em múltiplos de 5.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 5 | |||||
| Partes | |||||
| 360 | : | 5 | = | 72 | graus |
| 360 | : | 10 | = | 36 | graus |
| 360 | : | 20 | = | 18 | graus |
| 360 | : | 40 | = | 9 | graus |
| 360 | : | 80 | = | 4,5 | graus |
| 160 | 2,25 | ||||
| 320 | 1,125 | ||||
| 640 | 0,5625 | ||||
| www.osfantasticosnumerosprimos.com.br | |||||
Divisão de circunferência em múltiplos de 9.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 9 | |||||
| Partes | |||||
| 360 | : | 9 | = | 40 | graus |
| 360 | : | 18 | = | 20 | graus |
| 360 | : | 36 | = | 10 | graus |
| 360 | : | 72 | = | 5 | graus |
| 360 | : | 144 | = | 2,5 | graus |
| 288 | 1,25 | ||||
| 576 | 0,625 | ||||
| www.osfantasticosnumerosprimos.com.br | |||||
Divisão de circunferência em múltiplos de 15.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 15 | |||||
| Partes | |||||
| 360 | : | 15 | = | 24 | graus |
| 360 | : | 30 | = | 12 | graus |
| 360 | : | 60 | = | 6 | graus |
| 360 | : | 120 | = | 3 | graus |
| 360 | : | 240 | = | 1,5 | graus |
| 480 | 0,75 | ||||
| www.osfantasticosnumerosprimos.com.br | |||||
Divisão de circunferência em múltiplos de 45.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 45 | |||||
| Partes | |||||
| 360 | : | 45 | = | 8 | graus |
| 360 | : | 90 | = | 4 | graus |
| 360 | : | 180 | = | 2 | graus |
| 360 | : | 360 | = | 1 | grau |
| 360 | : | 720 | = | 0,5 | graus |
| www.osfantasticosnumerosprimos.com.br | |||||
Autor: Ricardo Silva - outubro/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato