


Três são os pontos notáveis em um triângulo retângulo:
Ortocentro,
Incentro e
Baricentro.
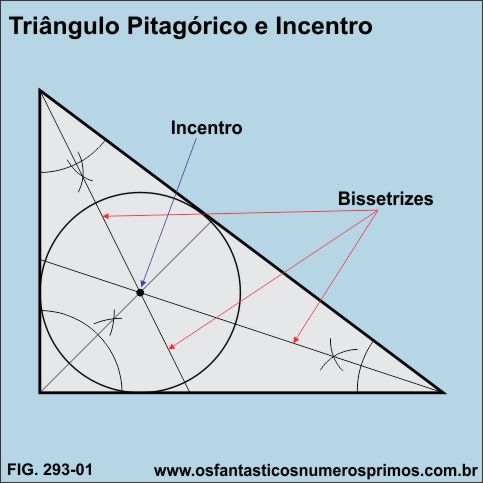
Incentro de um triângulo é o ponto onde as três bissetrizes se cruzam e que também é o centro da circunferência inscrita no triângulo.
Bissetriz de um triângulo é o segmento de reta que parte de um vértice, dividindo o ângulo interno em duas partes, até o lado oposto desse vértice.
Todo triângulo possuem três bissetrizes que se cruzam em um mesmo ponto, chamado de Incentro.
Triângulos Retângulos Pitagóricos são triângulos retângulos formados por conjuntos de três números inteiros que possuem relação com o Teorema de Pitágoras: a²=b²+c², os quais são denominados de Ternos Pitagóricos.
A circunferência inscrita em um Triângulo Retângulo Pitagórico também possui uma propriedade especial, pois tanto o seu raio quanto o seu diâmetro são constituídos por números inteiros e que também tem relação com o terno pitagórico que forma o respectivo triângulo retângulo.
A tabela abaixo apresenta os 15 primeros Ternos Pitagóricos gerados por meio das Fórmulas de Euclides:
a = m² - n²
b = 2mn
c = m² + n²
onde:
m > n (m tem que ser maior que n)
m e n tem que ser primos entre si
Observação importante:
As Fórmulas de Euclides não geram ternos pitagóricos derivados ímpares.
As Fórmulas de Euclides geram ternos pitagóricos derivados da seguinte forma: o dobro, do dobro, do dobro, do dobro e assim sucessivamente de um terno pitagórico primitivo.
Exemplos de Ternos Pitagóricos derivados do terno 3 - 4 - 5:
6 - 8 - 10;
12 - 16 - 20;
24 - 32 - 40...
Os ternos pitagóricos em destaque (cor amarelo) são Ternos Pitagóricos Primitivos de ordem triangular, isto é, suas ordens / posições correspondem a números triangulares, que são a base de estudos publicados no livro digital Ternos Pitagóricos e Sequências Numéricas.
Com ternos pitagóricos são possíveis de se contruirem infinitos triângulos retângulos de lados com números inteiros.
| Posições de Ternos Pitagóricos | |||
|---|---|---|---|
| posição/ | |||
| ordem | Ternos Pitagóricos | ||
| 1 | 3 | 4 | 5 |
| 2 | 8 | 6 | 10 |
| 3 | 5 | 12 | 13 |
| 4 | 15 | 8 | 17 |
| 5 | 12 | 16 | 20 |
| 6 | 7 | 24 | 25 |
| 7 | 24 | 10 | 26 |
| 8 | 21 | 20 | 29 |
| 9 | 16 | 30 | 34 |
| 10 | 9 | 40 | 41 |
| 11 | 35 | 12 | 37 |
| 12 | 32 | 24 | 40 |
| 13 | 27 | 36 | 45 |
| 14 | 20 | 48 | 52 |
| 15 | 11 | 60 | 61 |
| www.osfantasticosnumerosprimos.com.br | |||
A tabela abaixo apresenta o Terno Pitagórico Primitivo 3-4-5 e os seus 3 primeros ternos pitagóricos derivados.
O fator de multiplicação é ao mesmo tempo uma potência de base 2 que multiplicados por 3-4-5 geram ternos derivados que são o dobro, do dobro, do dobro do terno primitivo.
Esses fatores são os elementos que determinam também as medidas dos raios e diâmetros nas circunferências inscritas em triângulos retângulos pitagóricos.
Os fatores de multiplicação (potências de base 2) ao mesmo tempo se referem a ordem / posição de cada terno pitagórico derivado do Terno Pitagórico 3-4-5 e também é a diferença entre os respectivos termos de cada terno pitagórico.
Diferença entre os termos do Terno Pitagórico 3-4-5
5 - 4 = 1
4 - 3 = 1
Diferença entre os termos do Terno Pitagórico 6-8-10
10 - 8 = 2
8 - 6 = 2
| Terno Pitagórico 3-4-5 | |||
|---|---|---|---|
| e derivados | |||
| fator | catetos | ||
| multiplicação | menor | maior | hipotenusa |
| potências | |||
| de base 2 | |||
| 1 | 3 | 4 | 5 |
| 2 | 6 | 8 | 10 |
| 4 | 12 | 16 | 20 |
| 8 | 24 | 32 | 40 |
| www.osfantasticosnumerosprimos.com.br | |||
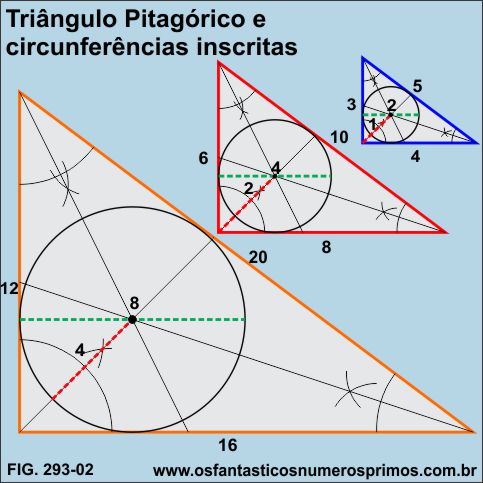
Conforme a Figura 293-02, observa-se que as medidas dos raios e diâmetros das circunferências inscritas nos triângulos pitagóricos derivados do terno 3-4-5 apresentam correspondências com cada fator de multiplicação pois:
a) as medidas dos raios são potências de base 2;
b) os diâmetros são os dobros de potências de base 2.
O diâmetro é 1/2 do cateto maior
Triângulo Retângulo Pitagórico 3-4-5:
4 : 2 = 2
Triângulo Retângulo Pitagórico 6-8-10:
8 : 4 = 2
Triângulo Retângulo Pitagórico 12-16-20:
16 : 8 = 2
O raio é 1/3 do cateto menor.
Triângulo Retângulo Pitagórico 3-4-5:
3 : 1 = 3
Triângulo Retângulo Pitagórico 6-8-10:
6 : 2 = 3
Triângulo Retângulo Pitagórico 12-16-20:
12 : 4 = 3
O raio é 1/5 da hipotenusa.
Triângulo Retângulo Pitagórico 3-4-5:
5 : 1 = 5
Triângulo Retângulo Pitagórico 6-8-10:
10 : 2 = 5
Triângulo Retângulo Pitagórico 12-16-20:
20 : 4 = 5
Triângulo Retângulo Pitagórico 3-4-5:
3 + 2 = 5
Triângulo Retângulo Pitagórico 6-8-10:
6 + 4 = 10
Triângulo Retângulo Pitagórico 12-16-20:
12 + 8 = 20
Triângulo Retângulo Pitagórico 3-4-5:
4 + 1 = 5
Triângulo Retângulo Pitagórico 6-8-10:
8 + 2 = 10
Triângulo Retângulo Pitagórico 12-16-20:
16 + 4 = 20
Triângulo Retângulo Pitagórico 3-4-5:
2 + 1 = 3
Triângulo Retângulo Pitagórico 6-8-10:
4 + 2 = 6
Triângulo Retângulo Pitagórico 12-16-20:
8 + 4 = 12
A tabela abaixo apresenta os 5 primeiros Ternos Pitagóricos Primitivos de ordem triangular.
| Ternos Pitagóricos | |||
|---|---|---|---|
| de ordem Triangular | |||
| ordem / | catetos | ||
| posição | menor | maior | hipotenusa |
| 1 | 3 | 4 | 5 |
| 2 | 5 | 12 | 13 |
| 3 | 7 | 24 | 25 |
| 4 | 9 | 40 | 41 |
| 5 | 11 | 60 | 61 |
| www.osfantasticosnumerosprimos.com.br | |||
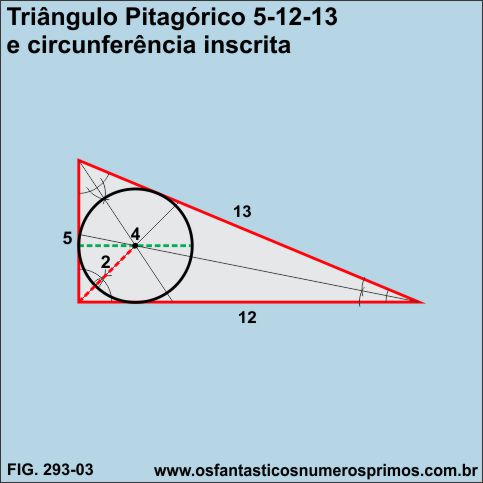
O segundo terno pitagórico primitivo é 5-12-13.
A sua posição / ordem é de número 2.
A medida do raio da circunferência circunscrita no triângulo retângulo pitagórico 5-12-13 é 2.
A medida do diâmentro da circunferência circunscrita no triângulo retângulo pitagórico 5-12-13 é 4.
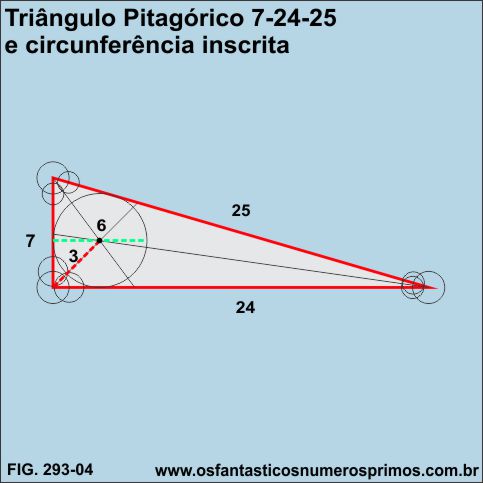
O terceiro terno pitagórico primitivo é 7-24-25.
A sua posição/ordem é número 3.
| Ternos Pitagóricos | |||
|---|---|---|---|
| de ordem Triangular | |||
| posição/ | catetos | ||
| ordem | menor | maior | hipotenusa |
| 1 | 3 | 4 | 5 |
| 2 | 5 | 12 | 13 |
| 3 | 7 | 24 | 25 |
| 4 | 9 | 40 | 41 |
| 5 | 11 | 60 | 61 |
| www.osfantasticosnumerosprimos.com.br | |||
A medida do raio da circunferência circunscrita no triângulo retângulo pitagórico 7-24-25 é 3.
A medida do diâmentro da circunferência circunscrita no triângulo retângulo pitagórico 5-12-13 é 6.
A Fórmula do Raio da circunferência inscrita em triângulo retângulo, a seguir, foi apresentada na vídeo-aula do Professor Fábio Machado Foncesca do Delta Medicina Online, postada no YouTube em janeiro de 2021, tive a oportunidade de vê-la em setembro de 2021.
Segundo o Professor, está fórmula é exclusiva para triângulo retângulo.
Confesso que não a conhecia, sendo uma novidade para mim e o interessante, sendo ela exclusiva para triângulo retângulo, é uma forma de comprovar a relação entre Terno Pitagórico e a sua ordem / posição com a medida do raio da circunferência inscrita em triângulo retângulo pitagórico.
A metade da soma dos catetos subtraída da hipotenusa é igual ao raio da circunferência inscrita num triângulo retângulo escaleno.
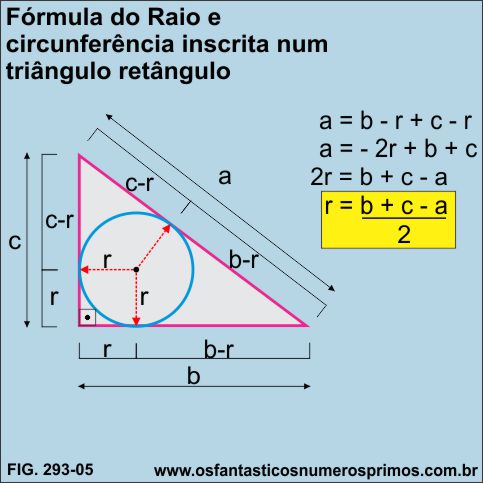
Fonte: https://www.youtube.com
5 = 4 - r + 3 - r
5 = -2r + 4 + 3
2r = (4 +3) - 5
2r = 7 - 5
r = 2/2
r = 1
13 = 12 - r + 5 - r
13 = -2r + 12 + 5
2r = (12 +5) - 13
2r = 17 - 13
r = 4/2
r = 2
25 = 24 - r + 7 - r
25 = -2r + 24 + 7
2r = (24 +7) - 25
2r = 31 - 25
r = 6/2
r = 3
Há várias fórmulas para se calcular a área de uma região triangular, entre elas, a Fórmula de Heron de Alexandria (? - 50 a.C), matemático e inventor grego.
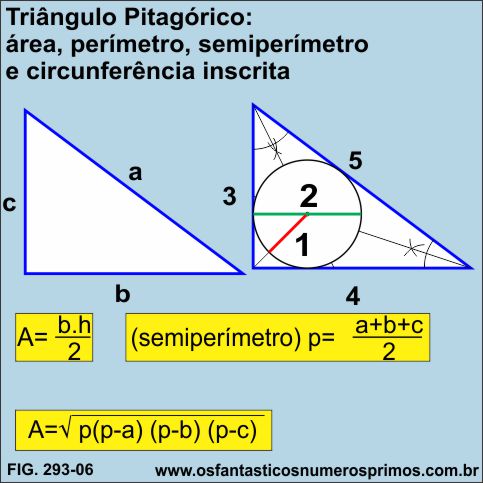
Sabendo duas medidas: base e altura de um triângulo, podemos conhecer a sua área usando a fórmula usual, que é mais simples.
Exemplo: Triângulo Pitagórico 3-4-5
| b.h | ||
| A | = | _____ |
| 2 |
| 4.3 | ||
| A | = | ____ |
| 2 |
| 12 | ||
| A | = | ____ |
| 2 |
| A | = | 6 |
Tendo-se as 3 medidas dos lados de um triângulo, calcula-se o semiperímetro e posteriormente a área:
Exemplo: Triângulo Pitagórico 3-4-5
| a + b + c | ||
| p | = | _________ |
| 2 |
| 5 + 4 + 3 | ||
| p | = | ________ |
| 2 |
| 12 | ||
| p | = | ___ |
| 2 |
| p | = | 6 |
A área (A) é igual a raiz quadrada do produto do semiperímetro pelas diferenças do semiperímetro por cada lado do triângulo.
| A | = | √p (p-a) (p-b) (p-c) |
| A | = | √6 (6-5) (6-5) (6-3) |
| A | = | √6 (1) (2) (3) |
| A | = | √6 (1) (2) (3) |
| A | = | √6 (6) |
| A | = | √36 |
| A | = | 6 |
A partir de cálculos de área, perímetro e semiperímetro num triângulo retângulo podemos obter diversas relações com circunferência inscrita no próprio triângulo retângulo:
Exemplo: Triângulo Pitagórico 3-4-5
área = 6
Perímetro = 12
semiperímetro = 6
a) o quociente da área pelo semiperímetro num triângulo retângulo tem como resultado o raio da circunfência inscrita:
| A : p = r |
6 : 6 = 1
b) o produto do semiperímetro pelo raio da circunfência inscrita num triângulo retângulo tem como resultado a área:
| A = p . r |
6 = 6 . 1
Autor: Ricardo Silva - outubro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato