


Tales de Mileto, (c.624-546 a.C.) foi filósofo, matemático, engenheiro e astrônomo da Grécia Antiga, considerado, por alguns, o primeiro filósofo ocidental, de ascendência fenícia, nasceu em Mileto, antiga colônia grega, na Ásia Menor, atual Turquia.
Tales é apontado como um dos sete sábios da Grécia Antiga.
Entre seus feitos, na área de geometria, estão:
a) Teorema de Tales (intersecção) - um feixe de retas paralelas que é intersectado por duas retas transversais formam segmentos proporcionais;
b) Teorema do círculo - todo triângulo inscrito numa semicircunfência é um triângulo retângulo;
c) determinou através de cálculos de segmentos proporcionais a altura de uma pirâmide por meio de sua sombra e a altura e sombra de uma estaca.
Com lápis, caneta ou outro instrumento que se possa riscar sobre determinado suporte como papel, madeira, etc., pode-se desenhar triângulos retângulos aleatórios, isto é, com quaisquer tamanhos e ângulos.
Mas não se pode afirmar que os triângulos desenhados são TRIÂNGULOS RETÂNGULOS DE 30, 60 E 90 GRAUS ou TRIÂNGULOS RETÂNGULOS PITAGÓRICOS.
Para poder afirmar que possuem determinados ângulos e medidas são necessários utilizar um TRANSFERIDOR e RÉGUA.
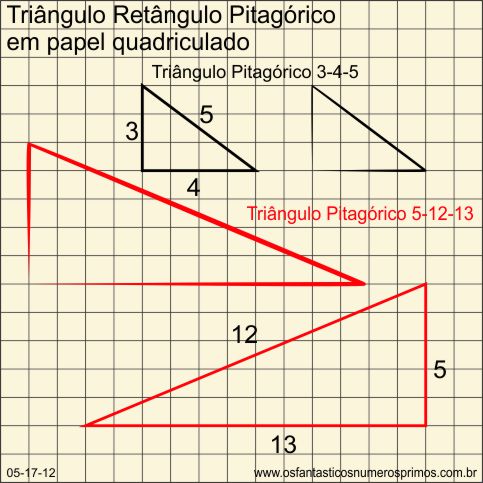
Sobre papel quadriculado, pode-se desenhar Triângulos Pitagóricos de quaisquer comprimentos à mão-livre, pois os lados de um triângulo retângulo pitagórico são formados por ternos pitagóricos, isto é, conjunto de 3 número inteiros que satisfazem ao Teorema de Pitágoras.
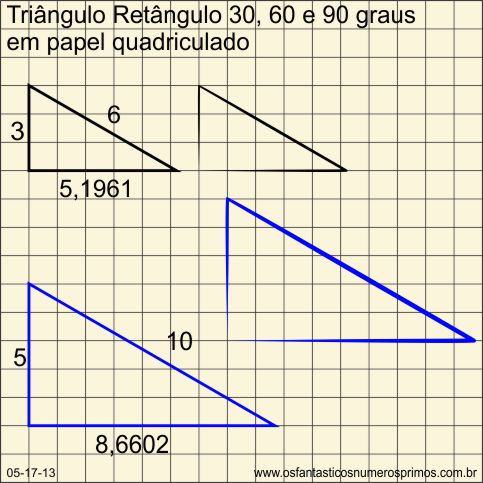
Sobre papel quadriculado, pode-se tentar desenhar triângulos retângulos de 30, 60 e 90 graus aproximados, à mão-livre.
Triângulo retângulo de 30, 60 e 90 graus possuem 2 lados cujas medidas são números inteiros e um lado com medida de número irracional, isto é, número decimal, não periódico e infinito.
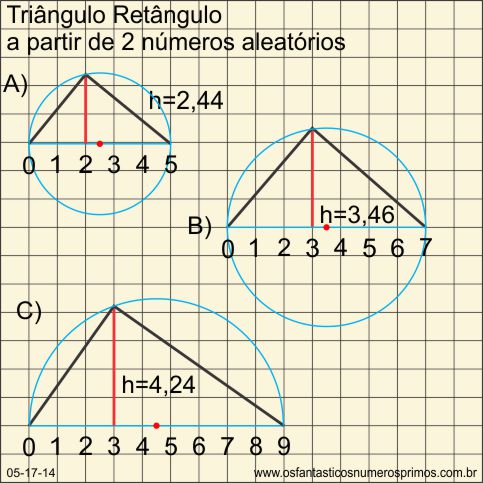
Triângulos retângulos também podem ser construídos escolhendo-se 2 números aleatóriamente, confome exemplo a seguir com uma reta numerada ou papel quadriculado:
Exemplo A)
a) Números escolhidos 2 e 3;
b) soma-se os dois números
2 + 3 = 5;
c) faz-se uma reta numerada de 5 unidades;
d) marca-se o ponto 2 na reta numerada;
e) multiplica o 2 por 3;
2 x 3 = 6
f) extrai-se a raiz quadrada de 6;
√6= 2,449...
g) a partir do ponto 2, traça-se uma perpendicular de medida 2,44 de altura;
h) una com seguimentos de reta a extremidade da reta numerada ao extremo da perpendicular, formando a figura de um triângulo retângulo;
i) determina-se a média aritmética de 2 e 3;
( 2 + 3 ) / 2 = 2,5
j) na reta numerada de 5 unidades, marque o ponto médio de 2,5 unidades;
k) com a ponta seca do compasso no ponto médio e abertura até a extremidade da reta numerada faça uma circunferência.
l) a circunferência intersecta os ângulos do triângulo retângulo.
Deixa-se os exemplos B) e C) ao Sr. estimado, Visitante, para treinamento!
Pode-se desenhar um triângulo inscrito numa circunferência, utilizando régua não graduada e compasso das seguintes formas:
a) traça-se duas retas perpendiculares;
b) com abertura qualquer do compasso, ponta seca no cruzamento da retas, desenha-se uma circunferência;
c) com mesma abertura do compasso, na intersecção da reta vertical com a circunferência, na parte inferior da circunferência, coloca-se a ponta seca e traça-se um arco;
d) estes procedimentos, faz com que se determinem 3 divisões de 120 graus na circunferência;
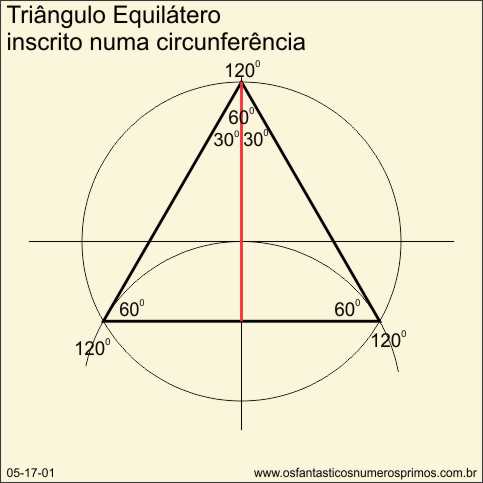
e) unindo-se os pontos das três divisôes com seguimentos de retas, constrói-se um triângulo equilátero.
Traçando-se um segmeno perpendicular da base ao vértice superior, obtem-se dois triângulos retângulos de 30, 60 e 90 graus.
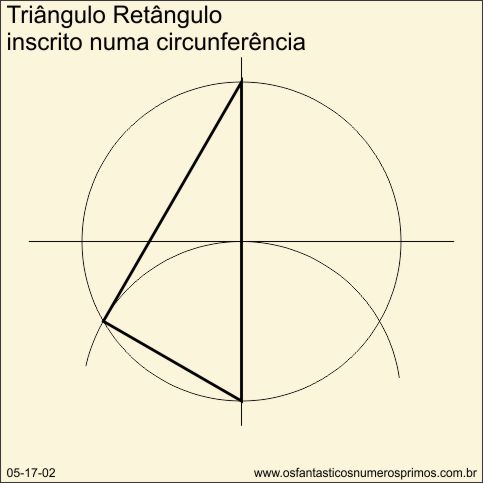
Com a mesma base e etapas de construções da (fig. 05-17-01), pode-se desenhar um triângulo retângulo de 30, 60 e 90 graus cuja hipotenusa tem a mesma medida do diâmetro da circunferência.
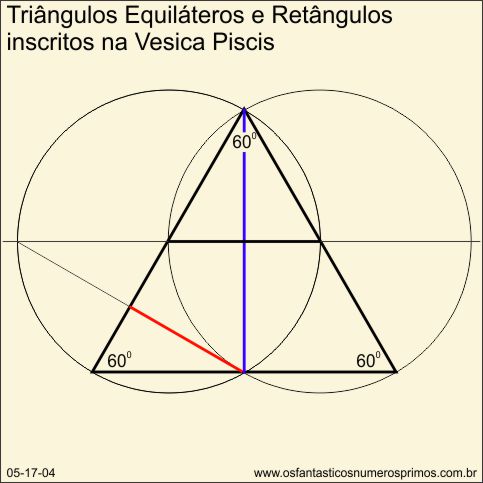
Vesica Piscis é uma construção geométrica com duas circunferências, de tal modo, que o centro de uma está na cincunferência da outra.
A Vesica Piscis é uma base de construção com a qual se pode desenhar figuras geométrias diversas; por meio dela, são possíveis de se construirem polígonos sequênciais de lados de mesma medida, utilizando somente compasso e régua não graduada.
No exemplo a seguir, são apresentados detalhes de constuções de triângulos equiláteros e triângulos retângulos de 30, 60 e 90 graus proporcionais.
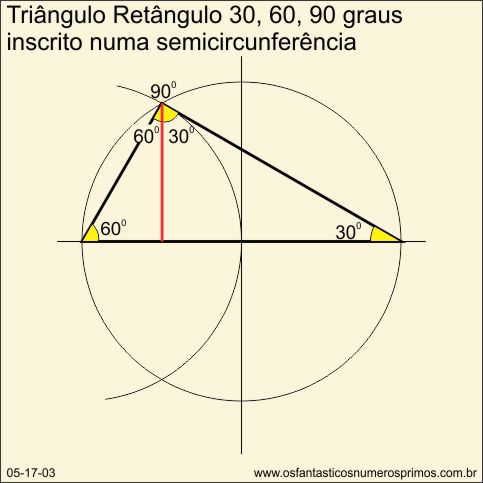
O triângulo retângulo de 30, 60 e 90 graus quando inscrito numa semicircunferência se encaixa perfeitamente na forma da "meia-lua" que é formada pela própria semicircunferência.
O vértice do ângulo de 90 graus e o seguimento da altura relativa à hipotenusa se encontram justamente na intersecção com a semicircunferência.
O seguimento da altura relativa à hipotenusa, parte do ponto médio do raio da semicircunferência até um ponto da própria semicircunferência.
Propriedades estas, que não acontecem com triângulos cujos ângulos agudos diferem de 30 e 60 graus.
Outra característica intrínsica do triângulo retângulo de 30, 60 e 90 graus e que eles são submúltiplos do número composto 360.
O triângulo retângulo de ângulos de 30, 60 e 90 graus, além de suas propriedades métricas, possui também propriedades trigonométricas.
A razão entre a medida do cateto oposto pela hipotenusa é constante, isto é, vale 1/2, denominada de seno de 30 graus.
"A medida do cateto oposto é a metade da medida da hipotenusa, ou a medida da hipotenusa é o dobro da medida do cateto oposto".
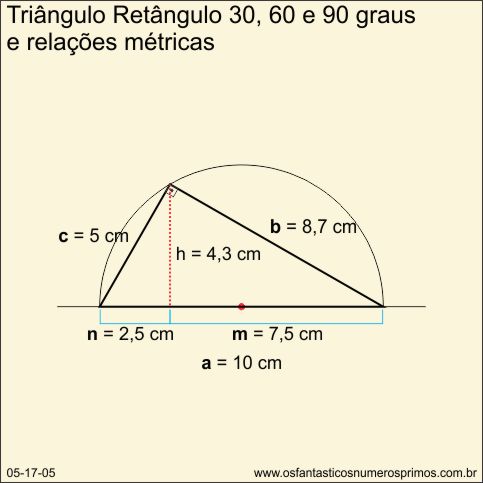
Pode-se determinar diversas medidas em relação aos lados quanto as partes do triângulo retângulo de 30, 60 e 90 graus.
| Lado | representação | medida | quadrado |
| hipotenusa | a | 10 | 100 |
| cateto maior | b | 8,7 | 75,6 |
| cateto menor | c | 5 | 25 |
| projeção do cateto menor | m | 2,5 | |
| projeção do cateto maior | n | 7,5 | |
| altura da hipotenusa | h | 4,3 | 18,75 |
Teorema de Pitágoras
a 2 = b 2 + c 2
10 2 = 8,7 2 + 5 2
100 = 75 + 25
100 = 100
Para se determinar a medida da projeção do cateto menor sobre a hipotenusa
c 2 / a = m
5 2 / 10 = 2,5
25 / 10 = 2,5
c 2 = a x m
Para se determinar a medida da projeção do cateto maior sobre a hipotenusa
b 2 / a = n
8,7 2 / 10 = 7,5
75,6 / 10 = 7,5
b 2 = a x n
Para se determinar a altura relativa à hipotenusa
h 2 = m x n
h 2 = 2,5 x 7,5
h 2 = 18,75
h = √18,75
h = 4,330...
Para se determinar a medida da hipotenusa
a = m + n
10 = 2,5 + 7,5
10 = 10
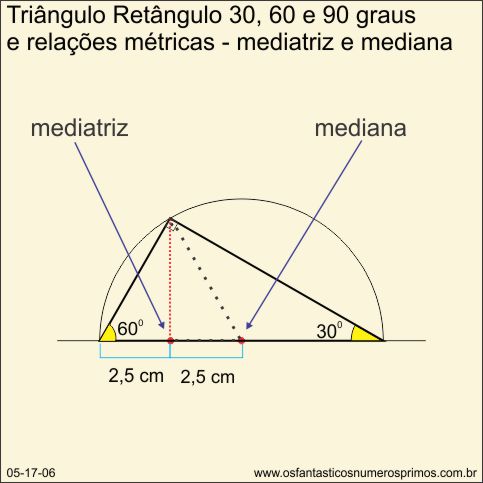
A partir da mediatriz (ponto médio de um segmento de reta) do raio da semicircunferência, determina-se a altura relativa à hipotenusa, outra propriedade que caracteriza um triângulo retângulo de 30, 60 e 90 graus.
Traçando-se a mediana (segmento de reta do vértice ao ponto médio do diâmetro), determina-se um triângulo equilátero inscrito no triângulo retângulo de 30, 60 e 90 graus.
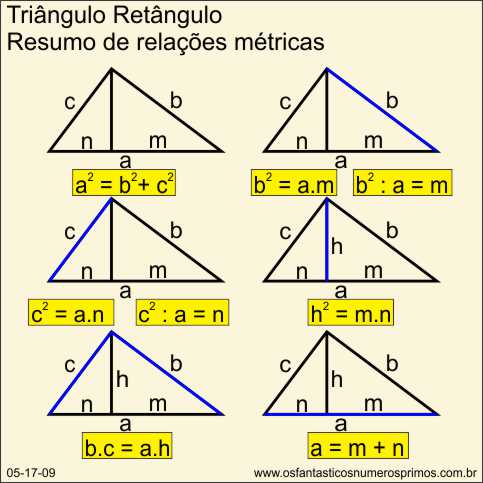
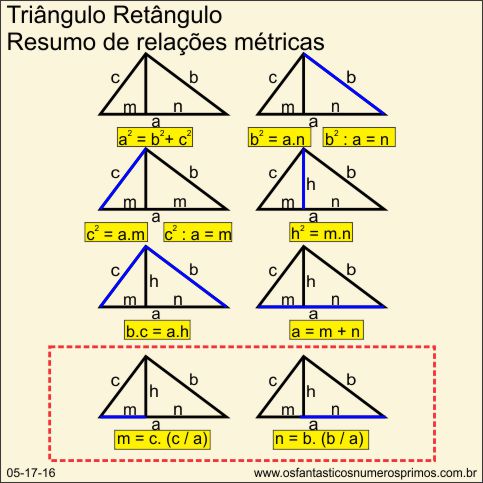
Resumo da relações métricas no triângulo retângulo.
Por meio das Fórmulas de Euclides de Alexandria, autor de Os Elementos, pode-se determinar ternos pitagóricos primitivos a partir de dois números primos entre si.
No livro digital Ternos Pitagóricos e Sequências Numéricas discorre sobre outros métodos de se formarem ternos pitagóricos, e entre eles, a partir de qualquer número ímpar maior que 1, pode-se determinar ternos pitagóricos primitivos.
Exemplo)
Terno Pitagórico a partir do número ímpar 3
a) 3 (cateto menor)
b) Quadrado de 3 = 9
c) 9 - 1 = 8
c) 8 : 2 = 4
d) 4 (cateto maior)
e) 4 + 1 = 5
f) 5 (hipotenusa)
Triângulos Pitagóricos são triângulos cujos lados são formados por três números inteiros, denominados de ternos pitagóricos.
Determinados triângulos pitagóricos possuem ângulos agudos de números primos.
O triângulo pitagórico 3-4-5 possui ângulos agudos de 37 e 53 graus e é o único triângulo retângulo escaleno formado por 3 números consecutivos cuja diferença entre eles é de 1 unidade.
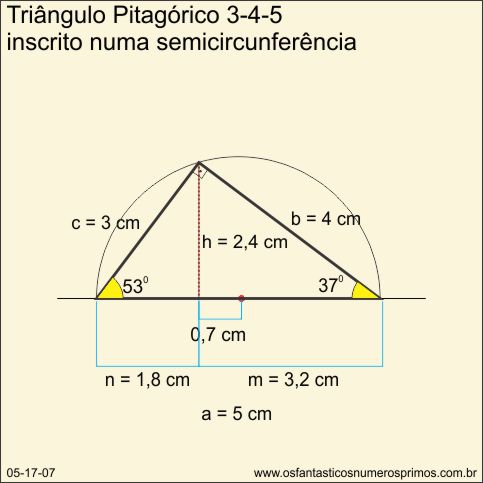
Na construção do Triângulos Pitagórico 3-4-5 com régua graduada e compasso obteve-se outras relações métricas interessantes nas projeções dos catetos e altura relativa à hipotenusa.
As relaçôes métricas aqui demonstradas, são novidades, pois até então, pesquisas realizadas sobre o assunto não apresentaram modelos matemáticos semelhantes.
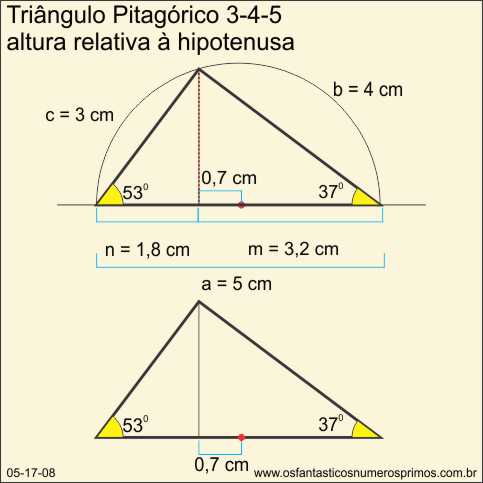
a) Subtraia o segmento n de m;
3,2 cm - 1,8 cm = 1,4 cm
b) divida 1,4 cm por 2;
1,4 : 2 = 0,7 cm
c) a partir do centro do diâmetro, para à esquerda, marque a diferença de 0,7 cm;
d) constrói-se uma perpendicular (altura relativa à hipotenusa);
e) liga-se com segmentos da extremidade do diâmetro à intersecção com a semicircunferência a altura relativa à hipotenusa.
Observação importante: esta propriedade também é válida para triângulo retângulo de 30, 60 e 90 graus.
a) 16 cm - 9 cm = 7cm
b) divide-se a diferença por 10;
7 cm : 10 = 0,7 cm
c) a partir do centro do diâmetro, para à esquerda, marca-se a diferença de 0,7 cm;
d) constrói-se uma perpendicular (altura relativa à hipotenusa);
e) liga-se com segmentos da extremidade do diâmetro à intersecção com a semicircunferência a altura relativa à hipotenusa.
Observação importante: esta propriedade também é válida para o triângulo retângulo de 30, 60 e 90 graus.
a) soma dos catetos;
3cm + 4 cm = 7cm
b) divide-se a soma por 10;
7 cm : 10 = 0,7 cm
c) a partir do centro do diâmetro, para à esquerda, marca-se a diferença de 0,7 cm;
d) constrói-se uma perpendicular (altura relativa à hipotenusa);
e) liga-se com segmentos das extremidades do diâmetro à intersecção com a semicircunferência à altura relativa à hipotenusa.
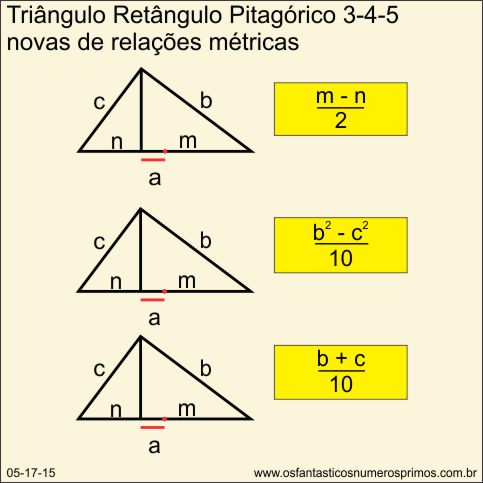
Assim como o triângulo retângulo formado pelo terno pitagórico 5-12-13 e os demais triângulos diferentes do triângulo pitagórico 3-4-5, basta calcular a diferença entre "n" e "m" e dividir por 2.
| n - m |
| _____ |
| 2 |
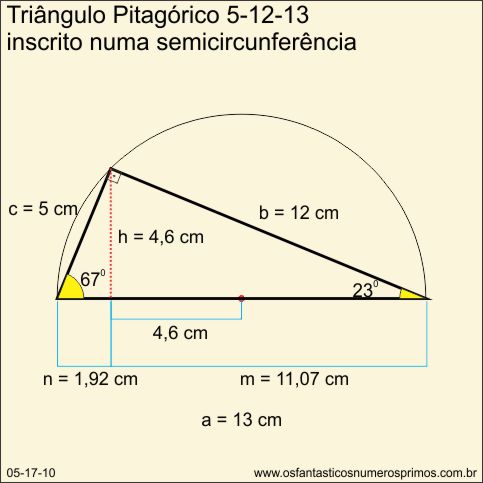
a) Subtraia o segmento m de n;
11,07 cm - 1,92 cm = 9,15 cm
b) divida 9,15 cm por 2;
9,15 : 2 = 4,57 cm (arredonda-se para 4,6 cm)
c) a partir do centro do diâmetro marque a diferença de 4,6 cm;
d) constrói-se uma perpendicular (altura relativa à hipotenusa);
e) liga-se com segmentos da extremidade do diâmetro à intersecção com a semicircunferência à altura relativa à hipotenusa.
Observação importante: esta propriedade também é válida para o triângulo retângulo de 30, 60 e 90 graus.
Recentemente, o Sr. Aristóteles Costa, Colaborador aqui do Web Site Os Fantásticos Números Primos, analisando o presente estudo constatou que no triângulo retângulo de lados 3-4-5 aparecem outras razões e que parecem também ser novas propriedades relacionadas às propriedades métricas e trigonométricas em triângulo retângulo, vejamos:
a) razão entre os quadrados dos catetos no Triângulo Pitagório 3-4-5;
| Razão entre os Quadrados dos Catetos | ||
| cateto maior | 16 | |
| ___ | 1,777778 | |
| cateto menor | 9 | |
| Razão entre os Quadrados dos Catetos | ||
| cateto maior | 9 | |
| ___ | 0,5625 | |
| cateto menor | 16 | |
b) razão entre as projeções dos catentos no Triângulo Pitagórico 3-4-5;
| Razão entre as Projeções dos Catetos | ||
| cateto maior | 3,2 | |
| ___ | 1,777778 | |
| cateto menor | 1,8 | |
| Razão entre as Projeções dos Catetos | ||
| cateto maior | 1,8 | |
| ___ | 0,5625 | |
| cateto menor | 3,2 | |
c) as razões 1,777778 formam uma proporção.
| 16 | 3,2 | |
| ___ | = | ___ |
| 9 | 1,8 |
d) as razões 0,5625 formam uma proporção.
| 9 | 1,8 | |
| ___ | = | ___ |
| 16 | 3,2 |
Outras propriedades constatadas em triângulos retângulos são:
a) o produto do cateto menor pelo seno tem como resultado a projeção do cateto menor (m) sobre a hipotenusa;
m = c ( c / a)
m = 3 x 0,6
m = 1,8
b) o produto do cateto maior pelo cosseno tem como resultado a projeção do cateto maior (n) sobre a hipotenusa ;
n = b ( b / a)
n = 4 x 0,8 =
n = 3,2
| Triângulo Retângulo 3-4-5 | |||||
| quadrado | |||||
| cateto Menor | c | 3 | 9 | ||
| quadrado | |||||
| cateto Maior | b | 4 | 16 | ||
| quadrado | |||||
| hipotenusa | a | 5 | 25 | ||
| seno | c / a | 3 | / | 5 | 0,6 |
| cosseno | b / a | 4 | / | 5 | 0,8 |
| tangente | c / b | 3 | / | 4 | 0,75 |
| projeção n | c^2 / 5 | 9 | / | 5 | 1,8 |
| projeção m | b^2 / 5 | 16 | 5 | 3,2 | |
| altura hipotenusa | h^2 = m.n | 1,8 | x | 3,2 | 2,4 |
| razão entre | b^2 / c^2 | 16 | / | 9 | 1,77 |
| quadrados catetos | |||||
| razão entre | n / m | 3,2 | 1,8 | 1,77 | |
| projeções n e m | |||||
| produto do cateto menor | c x sen | 3 | x | 0,6 | 1,8 |
| pelo seno | |||||
| produto do cateto maior | b x cos | 4 | x | 0,8 | 3,2 |
| pelo cosseno | |||||
| www.osfantasticosnúmerosprimos.com.br | |||||
| Triângulo Retângulo 5-12-13 | |||||
| quadrado | |||||
| cateto Menor | c | 5 | 25 | ||
| quadrado | |||||
| cateto Maior | b | 12 | 144 | ||
| quadrado | |||||
| hipotenusa | a | 13 | 169 | ||
| seno | c / a | 5 | / | 13 | 0,38 |
| cosseno | b / a | 12 | / | 13 | 0,92 |
| tangente | c / b | 5 | / | 12 | 0,41 |
| projeção n | c^2 / 5 | 25 | / | 13 | 1,92 |
| projeção m | b^2 / 5 | 144 | / | 13 | 11,07 |
| altura hipotenusa | h^2 = m.n | 1,92 | x | 11,07 | 4,61 |
| razão entre | b^2 / c^2 | 144 | / | 25 | 5,76 |
| quadrados catetos | |||||
| razão entre | n / m | 11,07 | / | 1,92 | 5,76 |
| projeções n e m | |||||
| produto do cateto menor | c x sen | 5 | x | 0,38 | 1,92 |
| pelo seno | |||||
| produto do cateto maior | b x cos | 12 | x | 0,92 | 11,07 |
| pelo cosseno | |||||
| www.osfantasticosnúmerosprimos.com.br | |||||
| Triângulo Retângulo 7-24-25 | |||||
| quadrado | |||||
| cateto Menor | c | 7 | 49 | ||
| quadrado | |||||
| cateto Maior | b | 24 | 576 | ||
| quadrado | |||||
| hipotenusa | a | 25 | 625 | ||
| seno | c / a | 7 | / | 25 | 0,28 |
| cosseno | b / a | 24 | / | 25 | 0,96 |
| tangente | c / b | 5 | / | 12 | 0,41 |
| projeção n | c^2 / 5 | 49 | / | 25 | 1,96 |
| projeção m | b^2 / 5 | 576 | / | 25 | 23,04 |
| altura hipotenusa | h^2 = m.n | 1,96 | x | 23,04 | 6,72 |
| razão entre | b^2 / c^2 | 576 | / | 49 | 11,75 |
| quadrados catetos | |||||
| razão entre | n / m | 23,04 | / | 1,96 | 11,75 |
| projeções n e m | |||||
| produto do cateto menor | c x sen | 7 | x | 0,28 | 1,96 |
| pelo seno | |||||
| produto do cateto | b x cos | 24 | x | 0,96 | 23,04 |
| maior pelo cosseno | |||||
| www.osfantasticosnúmerosprimos.com.br | |||||
| Triângulo retângulo 30-60-90 | |||||
| quadrado | |||||
| cateto Menor | c | 5 | 25 | ||
| quadrado | |||||
| cateto Maior | b | 8,66 | 74,99 | ||
| quadrado | |||||
| hipotenusa | a | 10 | 100 | ||
| seno | c / a | 5 | / | 10 | 0,5 |
| cosseno | b / a | 8,66 | / | 10 | 0,86 |
| tangente | c / b | 5 | / | 12 | 0,41 |
| projeção n | c^2 / 5 | 25 | / | 10 | 2,5 |
| projeção m | b^2 / 5 | 74,9956 | / | 10 | 7,49 |
| altura hipotenusa | h^2 = m.n | 2,5 | x | 7,49956 | 4,33 |
| razão entre | b^2 / c^2 | 74,9956 | / | 25 | 2,99 |
| quadrados catetos | |||||
| razão entre | n / m | 7,49956 | / | 2,5 | 2,99 |
| projeções m e n | |||||
| produto do cateto menor | c x sen | 5 | x | 0,5 | 2,5 |
| pelo seno | |||||
| produto do cateto maior | b x cos | 8,66 | x | 0,866 | 7,49 |
| pelo cosseno | |||||
| www.osfantasticosnúmerosprimos.com.br | |||||
O Web-Site Os Fantásticos Números Primos lança um desafio a você estimado visitante: de construir um triângulo pitagórico inscrito numa circunferência somente com régua não graduada e compasso semelhante ao triângulo retângulo de 30, 60 e 90 graus para ser publicado na Seção Texto do WebSite.
Enviando o seu estudo e modelo matemático da sua solução, para o nosso e:mail:
contato@osfantasticos
você receberá como cortesia:
O livro digital OS FANTÁSTICOS NÚMEROS PRIMOS
Veja a matérias:
005-texto-017-triangulos-pitagoricos-inscrito-semicircunferencia
005-texto-018-triangulo-pitagorico3-4-5-inscrito-semicircunferencia
sobre construções de triângulos.
Autor: Ricardo Silva - abril/2020
atualizado setembro/2025
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
LAWLOR, Robert. A Geometria Sagrada. Versão Brasileira: GVS, 1996
NAKAMURA, Keiji. Conjunto do números irracionais: a trajetória de um conteúdo não incorporado às práticas educacionais. Dissertação de Mestrado. Pontifícia Universidade Católica. São Paulo, 2008
SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces - As possilibilidades de construção - Dissertação de Mestrado. Universidade de Lisboa - Faculdade de Belas Artes, 2013.
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org/wiki/
https://pt.wikipedia.org/wiki/ https://pt.wikipedia.org/wiki/ Senhores Professores de Matemática,
Profissionais de Exatas e Entusiastas Matemáticos FAÇA A SUA SOLICITAÇÃO AGORA MESMO ATRAVÉS DO E-MAIL: Prezado visitante, o conteúdo do WebSite Os Fantásticos Números Primos está protegido por direitos autorais. O uso acadêmico e escolar está liberado, desde que informando ao autor o local e o meio em que será utilizado e divulgado, através do e-mail: contato@osfantasticosnumerosprimos.com.br O uso comercial é proibido.
Matérias relacionadas:
005-texto-005-triangulo-retangulo-figura-fantastica
005-texto-006-relacoes-metricas-triangulo-retangulo
005-texto-009-vesica-piscis-figuras-geometrica
005-texto-013-teorema-pitagoras-power-point-e-imagens-JPEG
005-texto-018-triangulo-pitagorico 3-4-5-inscrito-semicircunferencia
011-estudos-115-quadrados-dinamicos
011-estudos-116-triangulo-inscrito-em-um-quadrados
011-estudos-143-quadrado-inscrito-e-circunscrito-numa-circunferencia
011-estudos-157-raiz-quadrada-aproximada
011-estudos-251-teorema-de-pitagoras
011-estudos-603-altura-de-triangulo-retangulo-pitagorico
RECEBAM GRATUITAMENTE
O E-BOOK
TRIÂNGULO RETÂNGULO:





Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato