


Ao iniciarmos os estudos dos triângulos, deparamos com muitas informações, tais como códigos, fórmulas, modelos matemáticos, etc., que esta figura geométrica possui, devemos estudá-lo metodicamente cada assunto para ter uma compreensão geral das suas relações métricas e trigonométricas, pois o estudo do triângulo envolve também as outras figuras geométricas.
Nesta apresentação são demonstrados alguns métodos para auxilar nos estudos do triângulo retângulo.
Desenhe um triângulo retângulo, nomei os seus lados, marque as medidas dos seus lados e os seus respectivos quadrados e também seus vértices como na figura 1.
No exemplo, temos o famoso triângulo retângulo de lados 3, 4 e 5, com cada um dos seus lados identificados com cores diferente uma da outra.
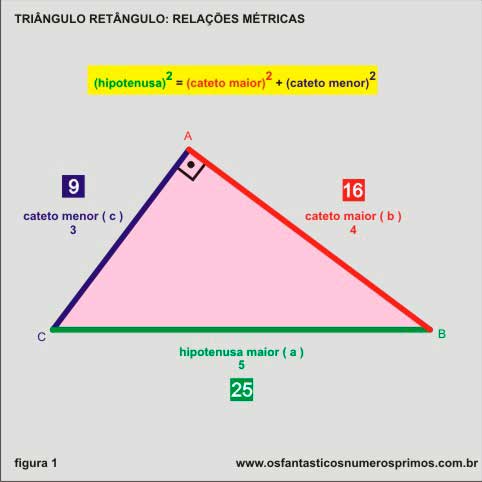
Utilizando o Teorema de Pitágoras (a²=b²+c²), que diz que "o quadrado da hipotenusa (a) é igual a soma dos quadrados dos catetos (b e c) ", pode-se determinar as medidas dos lados no triângulo retângulo.
Fazendo as substituições na fórmula com uso de cores e nomes, fica fácil fazer os cálculos nas equações a seguir.
| (hipotenusa a)² = (cateto maior b)² + (cateto menor c )² |
| (hipotenusa a)² = ( 4 )² + ( 3 )² |
| (hipotenusa a)² = 16 + 9 |
| (hipotenusa a)² = 25 |
| (hipotenusa a) = √25 |
| (hipotenusa a) = √5² |
| (hipotenusa a) = 5 |
| (hipotenusa a)² = (cateto maior b)² + (cateto menor c )² |
| (5)² = (cateto maior b)² + (3 )² |
| 25 = (cateto maior b)² + 9 |
| 25 - 9 = (cateto maior b)² |
| 16 = (cateto maior b)² |
| (cateto maior b)² = 16 |
| (cateto maior b)² = √16 |
| (cateto maior b)² = √4² |
| (cateto maior b)² = 4 |
| (hipotenusa a)² = (cateto maior b)² + (cateto menor c )² |
| (5)² = (4)² + (cateto menor c )² |
| 25 = 16 + (cateto menor c )² |
| 25-16 = (cateto menor c )² |
| 9 = (cateto menor c )² |
| (cateto menor c )² = 9 |
| (cateto menor c ) = √9 |
| (cateto menor c ) = √3² |
| (cateto menor c ) = 3 |
Traçando-se uma linha perpendicular da base (hipotenusa) até o vértice de 90 graus, determinamos a altura relativa à hipotenusa.
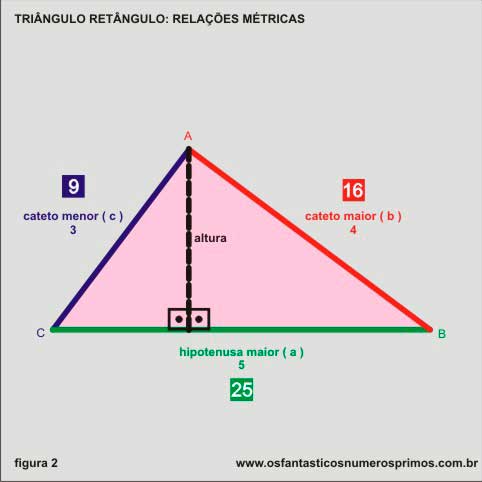
Traçando-se a altura relativa à hipotenusa, determinamos dois novos triângulos retângulos (um menor e outro médio) semelhantes e também as projeções dos catetos sobre a hipotenusa.
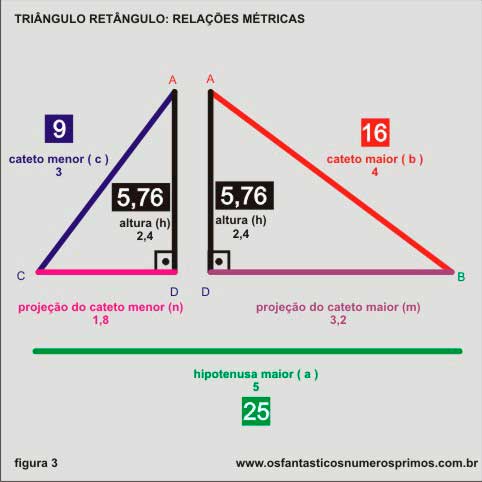
Divida o quadrado de 4 (16) do cateto maior pela medida hipotenusa.
| 16 : 5 = 3,2 (projeção do cateto maior m ) |
Reparem que, na criação dos dois novos triângulos: um menor e outro médio, os catetos se transformaram em hipotenusas que são os lados maiores dos triângulos retângulos. Na prática, estamos divindo o quadrado (16) da medida da hipotenusa do triângulo retângulo médio pela raiz quadrada da hipotenusa do triângulo retângulo maior.
Divida o quadrado de 3 (9) do cateto menor pela medida hipotenusa
| 9 : 5 = 1,8 (projeção do cateto menor n ) |
Reparem que, na criação dos dois novos triângulos: um menor e outro médio, os catetos se transformaram em hipotenusas que são os lados maiores dos triângulos retângulos. Na prática, estamos divindo o quadrado (9) da medida da hipotenusa do triângulo retângulo menor pela raiz quadrada da hipotenusa do triângulo retângulo maior.
Multiplicando as medidas das projeções dos catetos sobre a hipotenusa, obtemos o quadrado da medida da altura do triângulo retângulo.
| 3,2 (projeção do cateto maior) x 1,8 (projeção do cateto menor ) = 5,76 |
Extrai-se a raiz quadrada:
| √5,76 = 2,4 |
e tem-se a medida da altura do triângulo retângulo.
O produto dos catetos é igual ao produto da hipotenusa pela altura do triângulo retângulo.
| 3 x 4 = 12 |
O produto da hipotenusa pela altura do triângulo retângulo.
| 5 x 2,4 = 12 |
O produto dos quadrados dos catetos tem como resultado um número quadrado perfeito
9 x 16 = 144
O produto das medidas dos catetos tem com resultado a raiz quadrada do produto dos quadrados dos catetos.
3 x 4 = 12
O produto dos quadrados dos catetos e o quadrado da hipotenusa tem como resultado um número quadrado perfeito.
9 x 16 x 25= 3600
O produto das medidas dos catetos e da hipotenusa tem com resultado a raiz quadrada do produto dos quadrados dos catetos e do quadrado da hipotenusa.
3 x 4 x 5 = 60
Autor: Ricardo Silva
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato