capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Teorema de Pitágoras - 251

O triângulo é um figura geométrica singular pois:

1) é o único polígono que não possui diagonal;

2) é o único polígono que não possui simetria;

3) é o único polígono rígido, não é possível deformá-lo.

Mesmo sendo uma figura geométrica irregular, pois seus três lados apresentam medidas diferentes, ele possui propriedades algébricas, numéricas, geométricas e trigonométricas diversas.

Com figuras de triângulos retângulos escalenos são possíveis de se comporem outras figuras geométricas como quadradros, triângulos equiláteros, losangos, pentágonos, hexágonos, etc. e da mesma forma é possível decompor outras figuras geométricas em triângulos retângulos escalenos.

A partir de medidas que formam um triângulo retângulo escaleno são possíveis de se efetuarem cálculos para se saber, por exemplo, comprimentos de rios, alturas de montanhas, distâncias entre corpos celestes, etc.

No livro do professor de matemática estadunidense, Elisha Scott Loomis, The Pythagorean Proposition (segunda edição de 1940) são apresentadas mais de 500 demonstrações do Teorema de Pitágoras, entre as quais: demostrações algébricas, geométricas, quaterniônicas, dinâmicas e também 5 demonstrações de Quadrados Mágicos Pitagóricos produzidos entre os anos de 1898 a 1924 (data da primeira edição do livro).

No livro The Pythagorean Theorem Crown Jewel of Mathematics, edição de 2008, do engenheiro e professor estadunidense John C. Sparks, são apresentados diversos estudos de modelos matemáticos de composições e de arranjos de triângulos retângulos em que o autor brilhantemente "conjectura" de como pode ter sido originado a expressão geral a²= b² + c².

Teorema de Pitágoras e fórmula geral

Estudos históricos e arqueológicos nas regiões da antiga mesopotâmia e egípcia descobriram que estas civilizações já realizam cálculos utilizando-se de triângulos retângulos e da sequência numérica 3, 4 e 5.

Na região da mesopotâmia encontraram tabletes de barros com escrita cuneiforme (Plimpton 322) e que contêm ternos pitagóricos, conjunto de 3 números inteiros que se relacionam com os lados de triângulos retângulos.

Outra descoberta em tablete foi o seguinte texto: “4 é o comprimento, 5 é a diagonal. Qual é a altura? 4 vezes 4 é igual a 16, 5 vezes 5 dá 25. Tirando 16 de 25 o resto é 9. Quantas vezes quanto devo tomar para ter 9? 3 vezes 3 dá 9. 3 é a altura.” o que sugere conhecimento de relações numéricas no triângulo retângulo.

Do antigo egito, há o papiro do Cairo, que data de 300 a.C., encontrado em 1938, com diversos problemas matemáticos relacionados ao Teorema de Pitágoras.

Foi na civilização grega, especificamente com os pitagóricos, que foi demonstrado que a expressão geral a² = b²+ c² é válida para qualquer triângulo retângulo.

Teorema de Pitágoras e método geométrico

Modelo geométrico bastante prático para se provar o Teorema de Pitágoras é desenhar um triângulo retângulo de lados 3, 4, 5 e posteriormente desenhar quadrados quadriculados correspondentes às áreas dos lados do triângulo.

A soma dos quadradinhos da área verde (9) com os quadradinhos da área amarela (16) é igual a quantidade de quadradinhos da área vermelha (25).

9 + 16 = 25

teorema de pitágoras e o método geométrico

Teorema de Pitágoras e método algébrico

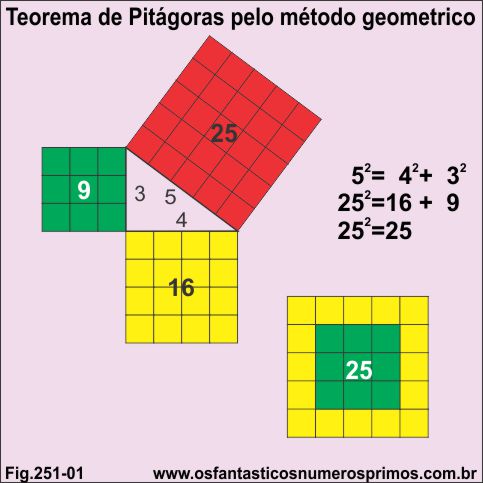
Com as medidas dos lados do triângulo retângulo descrito acima e utilizando a expressão algébrica chegamos ao mesmo resultado do método geométrico.

a² = b² + c²

5² = 4²+ 3²

25 = 16 + 9

25 = 25

Teorema de Pitágoras e fórmulas variantes

As demostrações a seguir estão publicadas no livro digital O triângulo retângulo - novas fórmulas de cálculos dos seus lados.

Estudos realizados com o Teorema de Pitágoras, triângulos retângulos e ternos pitagóricos foi possível desenvolver novas expressões algébricas sintéticas para se determinar medidas dos lados de triângulo retângulo, bem como a diagonal do quadrado e a diagonal do retângulo.

Teorema de Pitágoras e Fórmula Variante 1

Todo triângulo retângulo de ângulos 30, 60 e 90 graus, a medida da hipotenusa é o dobro da medida do cateto menor ou a medida do cateto menor é a metade da medida da hipotenusa.

Com Fórmula Variante 1 é possível determinar a medida do cateto maior por meio da medida do cateto menor de triângulo retângulo de ângulos 30, 60 e 90 graus.

teorema de pitágoras e formula variante 1

Teorema de Pitágoras e Fórmula Variante 2

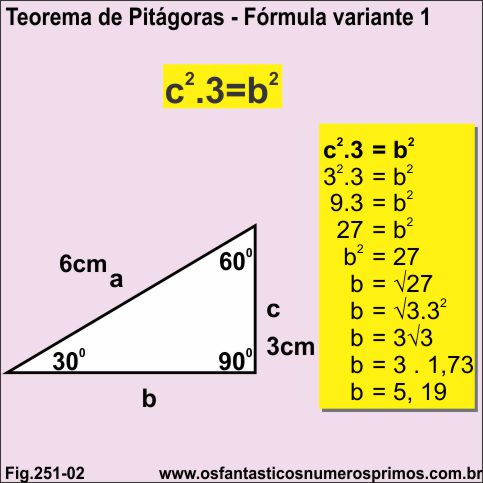
Todo triângulo retângulo de ângulos 30, 60 e 90 graus, a medida da hipotenusa é o dobro da medida do cateto menor ou a medida do cateto menor é a metade da medida da hipotenusa.

Com Fórmula Variante 2 é possível determinar a medida do cateto maior por meio da medida da hipotenusa de triângulo retângulo de ângulos 30, 60 e 90 graus.

teorema de pitágoras e fórmula variante 2

Teorema de Pitágoras e ternos pitagóricos

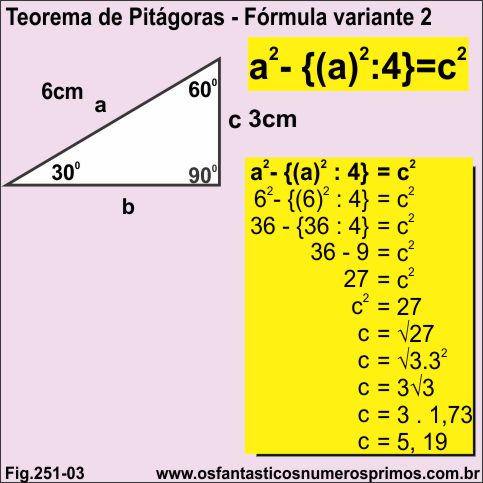
Ternos pitagóricos são grupos de 3 números inteiros que satisfazem ao Teorema de Pitágoras e consequentemente são possíveis de construirem triângulos retângulos escalenos.

O triângulo retângulo de lados 3, 4 e 5 demonstrado no íncio da matéria é formado por terno pitagórico primitivo.

Exemplos de ternos pitagóricos primitivos:

5, 12, 13

7, 24, 25

9, 40, 41

11, 60, 61

O livro digital Ternos Pitagóricos e Sequências Numéricas discorre de como gerar ternos pitagóricos por meio das clássicas Fórmulas de Euclides e também apresenta outros novos métodos.

Autor: Ricardo Silva - fevereiro /2020