


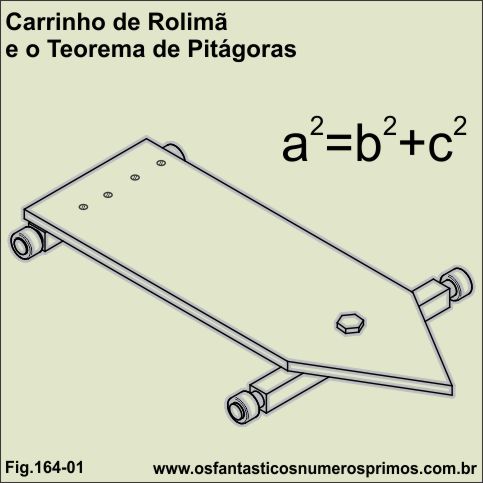
Carrinho de Rolimã se tornou popular quando ruas que eram de terras ou de paralelepípedos começaram a serem asfaltadas por prefeituras, e ruas que tinham um bom declive eram as felizardas para serem estreadas pela meninada, rapaziada e também por adultos.
Carrinho de Rolimã é um brinquedo de baixo custo é que pode ser construído com sobras de tábuas, caibros e sarrafos de madeiras descartadas geralmente de construções quando não mais utilizadas.
Os rolamentos (rolimãs) podem ser adquiridos em oficinas mecânicas, os quais servem para se montar os eixos: traseiro e frontal do carrinho.
O Carrinho de Rolimã de madeira é montado com um eixo traseiro fixado por parafusos na parte posterior do Assento/Base e um eixo dianteiro fixado por um só parafuso, de forma que podemos movimentá-lo com os pés para serem realizados manobras, curvas e derrapagens.
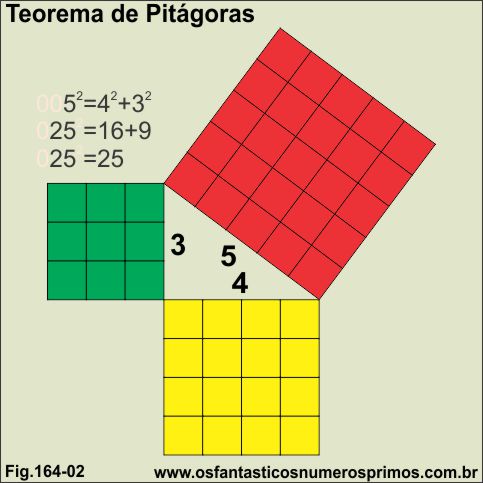
Em qualquer triângulo retângulo, o quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
Triângulo de lados 3 e 4, qual a medida da hipotenusa?
x2 = 32 + 42
x2 = 9 + 16
x2 = 25
x = √25
x = 5
R.: A medida da hipotenusa é 5.
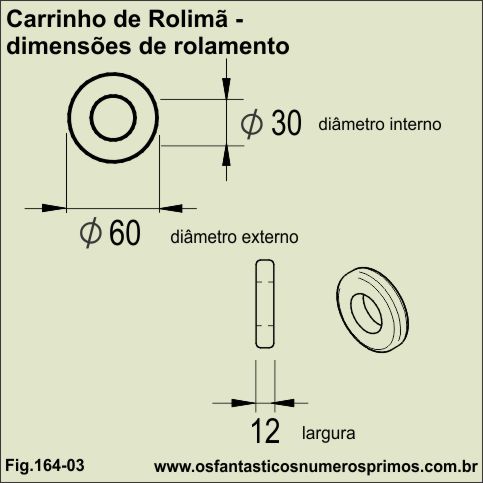
O rolamento possui três dimensões principais: diâmetro externo, diâmetro interno e a largura.
Vendo o rolamento de lado, o diâmetro externo nos dá a ideia de altura.
Vendo o rolamento de frente, podemos observar se ele é estreito ou largo.
O diâmetro interno é onde encaixamos os eixos do carrinho de rolimã.
Na figura 164-03 temos um desenho estilizado de rolamento com suas respectivas medidas.
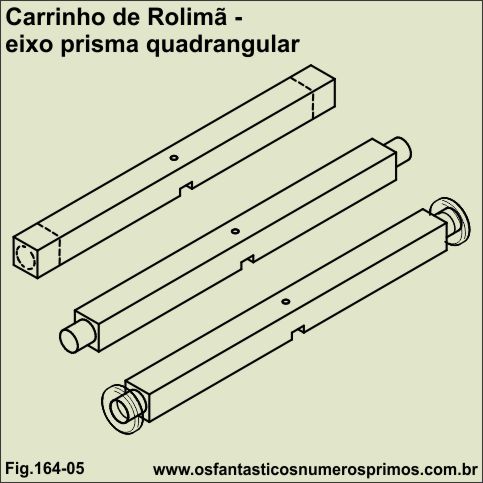
Há algumas formas de se confeccionar eixos para carrinho de rolimã, vejamos algumas delas para serem utilizadas no exemplo do rolamento com 30mm de diâmetro interno.
A primeira forma é tornear ou encontrar um eixo cilíndrico de madeira com a mesma medida do diâmetro interno de 30mm do rolamento.

A segunda forma é pegar um caibro um pouco maior que o diâmetro interno do rolamento, marca-se as extremidades conforme a figura 164-05 e posteriomente debastando e torneando-as para encaixar os rolamentos.
A terceira forma é pegar uma tábua um pouco maior que o diâmetro interno do rolamento, marca-se as extremidades conforme a figura 164-06 e posteriomente debastando e torneando-as para encaixar os rolamentos.
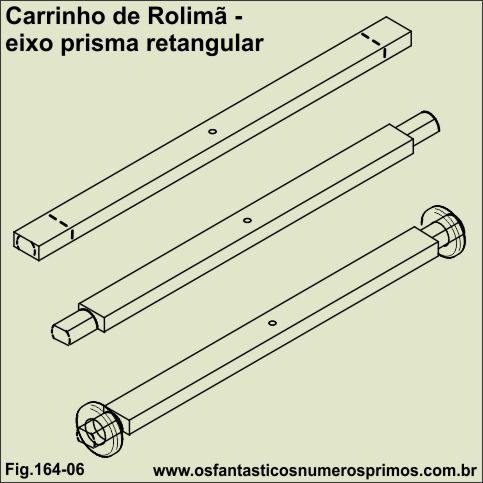
No figura 164-04 temos um exemplo de eixo cilíndrico com a medida exata do diâmetro interno para se fazer um encaixe perfeito dos rolamentos nas extremidades do eixo.
E se desejarmos utilizar eixo de prisma quadrangular de forma que seus cantos (vértices) encostem no diâmetro interno dos rolamentos fazendo um encaixe perfeito?
Quais devem ser os procedimentos?
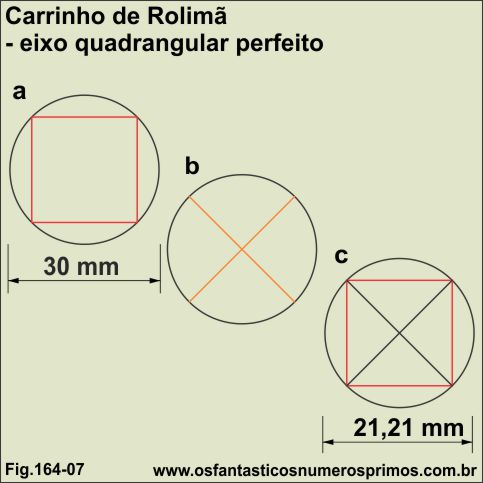
Para realizarmos esta tarefa, fazemos o uso da Geometria, através de modelos matemáticos das relações entre circunferência e o quadrado.
Para desenharmos um quadrado inscrito numa circunferência (desenho a), traçamos duas linhas perpendiculares (desenho b) e posteriomente unimos os pontos de encontros entre a circunferência e as linhas perpendiculares (desenho c), obtendo-se assim o quadrado inscrito.
Na figura 164-07, o diâmetro da circunferência (rolamento) é de 30mm e o quadrado (eixo) tem o seu lado de 21,21mm.
Os exemplos dos modelos matemáticos expostos anteriormente têm como fundamentação o famoso Teorema de Pitágoras.
a2 = b2 + c2
Obtivemos um quadrado inscrito de lado 21,21mm e queremos saber qual é a medida de sua diagonal, vejamos:
x2 = 21,212 + 21,212
x2 = 449,8641 + 449,8641
x2 = 899,7282
x = √899,7282
x = 29,995
x = 30 (arredondando o resultado)
R.: A medida da diagonal do quadrado é 30mm e que é a mesma medida do diâmetro interno do rolamento (rolimã).
Temos uma circunferência de diâmetro de 30mm e queremos saber qual a medida do lado de um quadrado inscrito.
30 : √2 =
30 : 1,4142 = 21,213
R.: A medida do lado do quadrado inscrito é 21,21mm.
Temos uma circunferência de diâmetro de 30mm e queremos saber qual a medida do lado de um quadrado circunscrito.
30 x √2 =
30 x 1,4142 = 42,426
R.: A medida do lado do quadrado circunscrito é 42,426 mm
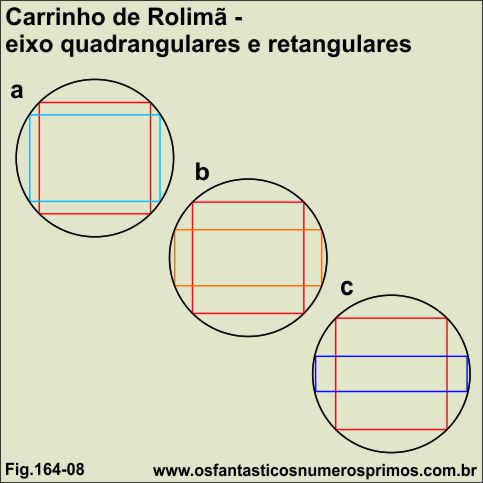
Através da utilização de modelos matemáticos, podemos projetar além de eixo quadrangular outros modelos de eixos retangulares de medidas diversas conforme exemplos da figura 164-08.
Autor: Ricardo Silva - abril/2018
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Conheça os projetos de carrinhos de rolimã desenvolvidos pela Encaixe Monte

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato