


No livro Pythagorean Proposition, Classics in Mathematics Education Serie do professor estadunidense Elisha Scott Loomis, cuja segunda edição foi lançada em 1940, encontra-se uma coletânea de 370 demonstrações do Teorema de Pitágoras entre elas: 109 demonstrações algébricas e 255 demonstrações geométricas.
Outro livro que também aborda demonstrações do Teorema de Pitágoras: Pythagorean Theorem – Crowl Jewl of Mathematics, edição de 2008, do engenheiro estadunidense John C. Sparks.
Acho desafiador, tentar criar novas demonstrações principalmente geométricas, ao mesmo tempo que se estimula o raciocínio faz a gente desenvolver novas soluções com sobreposição de figuras geométricas.
Duas demonstrações do Teorema de Pitágoras que me chamaram a atenção foram a que aparece no livro de matemática chinês Chou Pei Suan Ching e a do matemático hindu Bháskara.
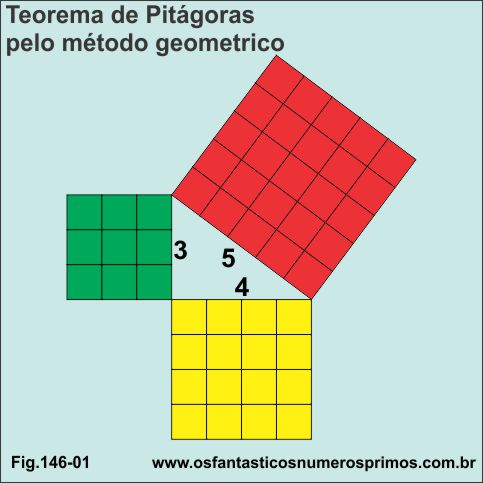
Modelo bastante utilizado para se demonstrar o Teorema de Pitágoras é construir um triângulo retângulo 3, 4 e 5 e desenhar nos seus lados quadrados quadriculados com as suas respectivas áreas.
Somando-se as quantidade de quadradinhos verdes mais os amarelos tem-se o total de vermelhos: 9 + 16 = 25.
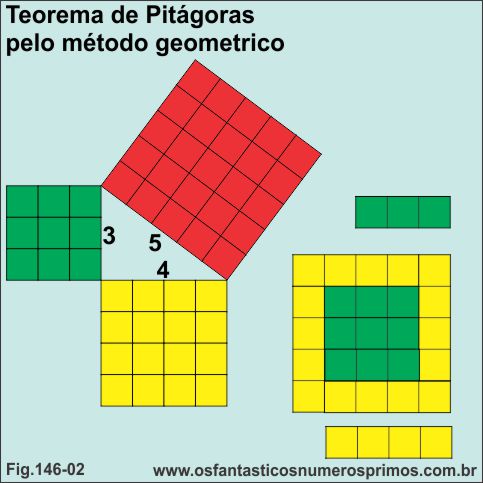
Nesta demonstração, montou-se o quadrado de área 25 com barrinhas quadriculadas de 3 x (1 x 3) mais 4 x (1 x 4), totalizando 25 quadradinhos.

Fonte: https://pt.wikipedia.org
Nesta demostração do livro Chou Pei Suan Ching, o quadrado de área 25 se encontra em um gabarito quadriculado e é formando por 4 triângulos retângulos cujas hipotenusas formam os lados do quadrado.
Cada triângulo retângulo possui a seguinte área:
3 x 4 = 12
12 / 2 = 6
Reparar que há um quadradinho no centro do quadrado maior.
Então, 4 triângulos x 6 (área) = 24
24 + 1 (quadradinho central) = 25 (área do quadrado maior)
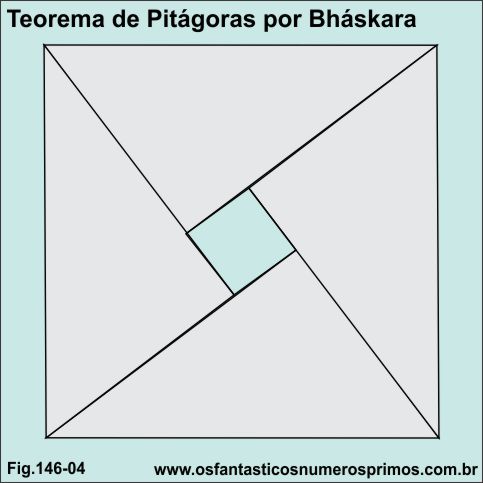
Na demostração feita pelo matemático hindu Bháskara Akaria, conforme relatos, ele simplesmente desenhou o modelo acima e tinha dito: Contemple!, Veja!, isto é, deixando para o observador verificar através de cálculos de que se tratava de uma demonstração do Teorema de Pitágoras, utilizando a montagem de 4 triângulos retângulos formando um quadrado.
Reparar que há um quadradinho no centro do quadrado maior.
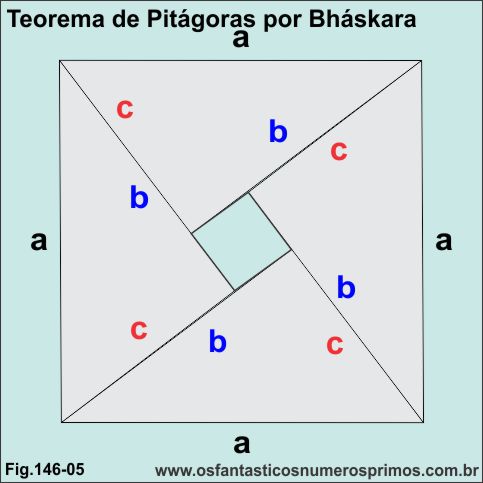
5a) Área do quadrado maior
a2
5b) Área dos 4 triângulos retângulos
4 . bc / 2
5c) Área do quadrado menor
(b-c)2
a2 = 4.bc / 2 + (b-c)2
a2 = 2bc + b2 - 2bc + c2
a2 = b2 + c2
Tanto na demonstração do Livro de matemática chinês Chou Pei Suan Ching e a de Bháskara, verifica-se que os triângulos que formam o quadrado, deixam um espaço vazio, isto é, um quadradinho e para que a relação entre os lados do triângulo funcionem os quadadrinhos pecisam ser somados.
Ai, vem a pergunta: Porque sobra o quadradinho?
Qual a relação entre as duas demostrações e a sobras dos quadradinhos, isto é, o espaço em branco.
E para mostrar porque sobram os quadradinhos, partir do primeiro exemplo 146-01, em que os lados do triângulo retângulo são construídos quadrados quadriculados com áreas dos respectivos lados, veremos o porque isto acontece.
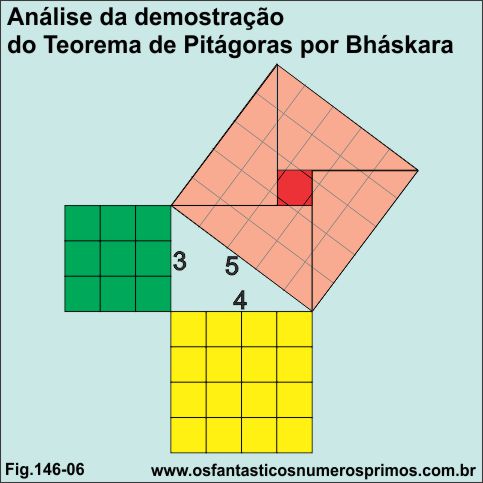
Utilizando como base a demostração 146-01, encaixa-se 4 triângulos 3, 4 e 5 sobre o quadrado de área 25, de forma que as hipotenusas alinhem-se sobre os lados do quadrado maior.
Verifica-se que também sobra uma área, isto é, sobra 1 quadradinho.
Por meio de estudos com da utilização de Ternos Pitagóricos Primitivos e Derivados, verificou-se que o espaço que sobra é a diferença entre os termos de um terno pitagórico e que corresponde ao lado do quadradinho.
Nos Ternos Pitagóricos 3, 4 e 5 e os seus derivados: 6, 8 e 10; 9, 12 e 15; 12, 16 e 20; e assim sucessivamente, a diferença entre os termos de cada terno é constante.
Exemplos:
Terno Primitivo: 3, 4 e 5 - diferença entre os termos é de 1 unidade.
Terno Derivado: 6, 8 e 10 - diferença entre os termos é de 2 unidades.
Terno Derivado: 9, 12 e 15 - diferença entre os termos é de 3 de unidades.
3, 4 e 5 é o primeiro Terno Pitagórico Primitivo.
5 - 4 = 1
4 - 3 = 1
1 quadradinho, 1 espaço ou 12 é o que sobrou na demonstração deste exemplo.
Áreas dos 4 triângulos
3 x 4 = 12
12 : 2 = 6
6 x 4 = 24
A área do quadrado maior 52 = 25
áreas dos triângulos mais a área do quadradinho: 24 + 1 = 25

Neste outro exemplo, temos um triângulo retângulo cujos lados são 6, 8 e 10 derivado do Terno Pitagórico Primitivo 3, 4, 5.
Sobrou uma área com 4 quadradinhos, cujo lado são 2 quadrados.
Direfença entre os termos do Terno Pitagórico Derivado:
10 - 8 = 2
8 - 6 = 2
22 = 4
Áreas dos 4 triângulos
8 x 6 = 48
48 : 2 = 24
24 x 4 = 96
A área do quadrado maior 102 = 100
áreas dos triângulos mais a área do quadradinho: 96 + 4 = 100
Autor: Ricardo Silva - outubro/2017
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato