


Os ternos pitagóricos quando aplicados em modelos matemáticos utilizando as figuras geométricas de triângulos retângulos observa-se regularidades quanto aos ângulos desses mesmos triângulos retângulos.
Os ternos pitagóricos por excelência são formados por números inteiros e consequentemente os seus respectivos números quadrados também são números inteiros.
Os ângulos agudos de determinados triângulos retângulos cujos lados são formados por ternos pitagóricos têm como ângulos agudos números primos.
Tanto o triângulo equilátero e o triângulo retângulo de ângulos 30º, 60º e 90º, tem uma vastíssima utilização em cálculos trigonométricos.
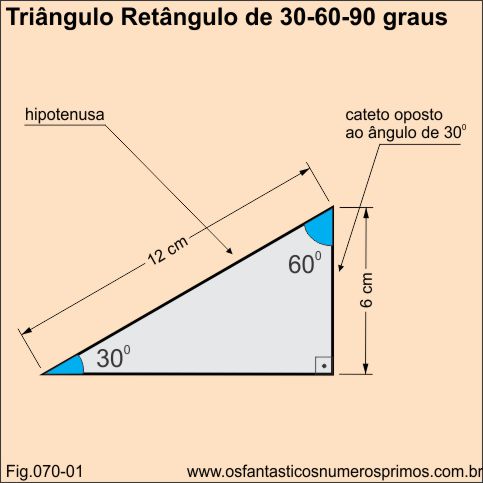
Uma das propriedades métricas interessantes no triângulo retângulo de ângulos 30º, 60º e 90º é que a medida da hipotenusa (o maior lado de um triângulo retângulo) é sempre o dobro da medida do cateto oposto (o menor lado) ao ângulo de 30º ou o menor lado é a metade da hipotenusa.
No exemplo abaixo, 6 é divisor de 12 e 12 é múltiplo de 6, há uma relação direta entre os números 6 e 12.
6 é a metade de 12.
12 é o dobro de 6.
Triângulo 1
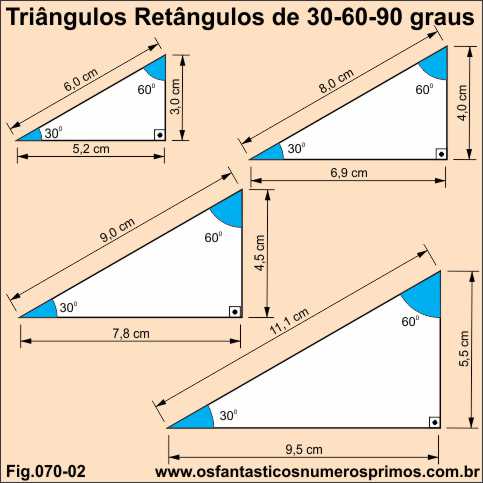
3 é divisor de 6 e 6 é múltiplo de 3 há uma relação direta entre os números 3 e 6.
3 é metade de 6.
6 é o dobro de 3.
Triângulo 2
4 é divisor de 8 e 8 é múltiplo de 4, há uma relação direta entre os números 4 e 8.
4 é a metade de 8.
8 é o dobro de 4.
Triângulo 3
4,5 é divisor de 9 e 9 é múltiplo de 4,5, há uma relação direta entre os números 4,5 e 9.
4,5 é a metade de 9.
9 é o dobro de 4,5.
Triângulo 4
5,5 é divisor de 11 e 11 é múltiplo de 5,5, há uma relação direta entre os números 5,5 e 11.
5,5 é a metade de 11.
11 é o dobro de 5,5.
Ternos pitagóricos são sequências numéricas que satisfazem a relação do Teorema de Pitágoras (a² = b² + c²), isto é, uma sequência de três números inteiros que utilizados no teorema tem como resultado um quadrado perfeito.
Uma outra característica em triângulos retângulos que têm seus lados com a sequência de ternos pitagóricos é que determinados triângulos retângulos têm seus ângulos agudos números primos.
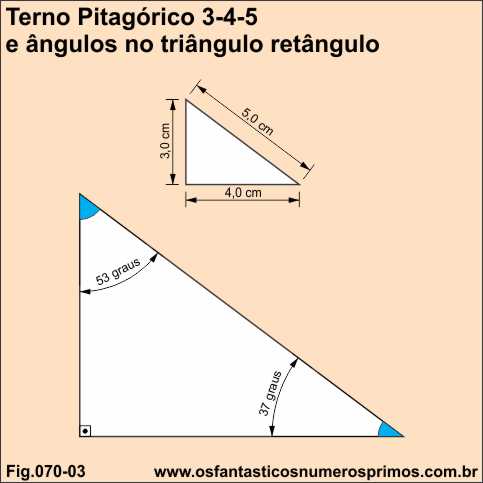
O triângulo retângulo de lados 3, 4, 5 é um triângulo pitagórico.
a² = b² + c²
5² = 4² + 3²
25 = 16 + 9
25 = 25
O seus ângulos agudos são 37 e 53.
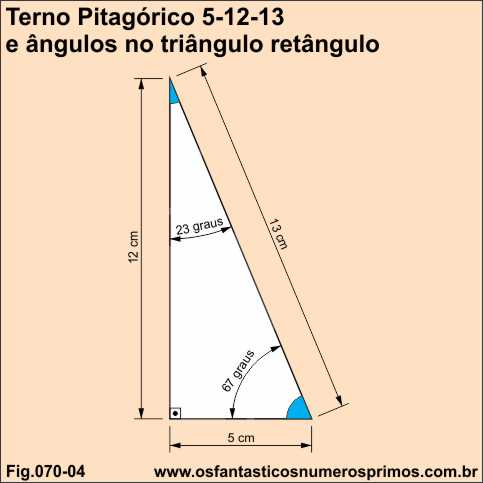
O triângulo retângulo de lados 5, 12, 13 é um triângulo pitagórico.
a² = b² + c²
13² = 12² + 5²
169 = 144 + 25
169 = 169
O seus ângulos agudos são 23 e 67.
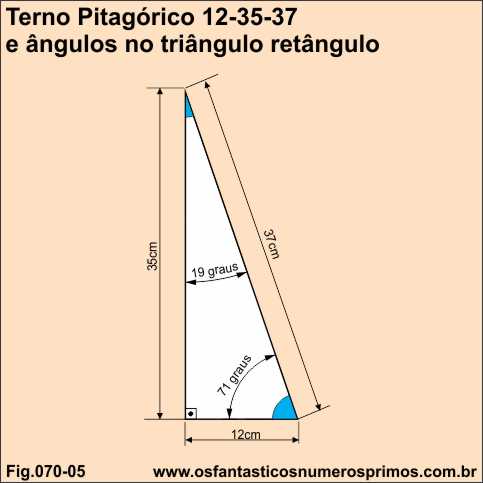
O triângulo retângulo de lados 12, 35, 37 é um triângulo pitagórico.
a² = b² + c²
37² = 35² + 12²
1369 = 1225 + 144
1369 = 1369
O seus ângulos agudos são 19 e 71.
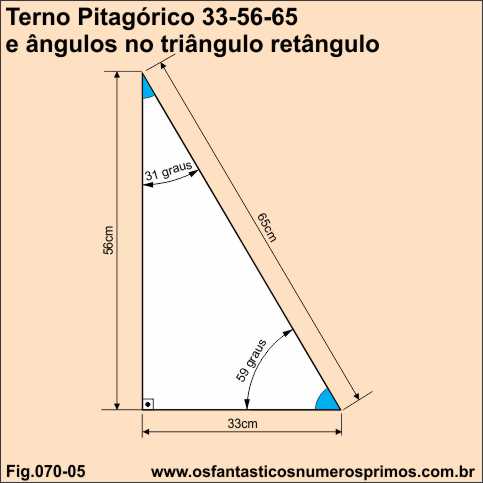
O triângulo retângulo de lados 33, 56, 65 é um triângulo pitagórico.
a² = b² + c²
65² = 56² + 33²
4225 = 3136 + 1089
4225 = 4225
O seus ângulos agudos são 31 e 59.
O Web-Site Os Fantásticos Números Primos lança um desafio a você estimado visitante: de construir um triângulo pitagórico inscrito numa circunferência somente com régua não graduada e compasso semelhante ao triângulo retângulo de 30, 60 e 90 graus para ser publicado na Seção Texto do WebSite.
Enviando o seu estudo e modelo matemático da sua solução, para o nosso e:mail:
contato@osfantasticos
você receberá como cortesia:
O livro digital OS FANTÁSTICOS NÚMEROS PRIMOS
Veja as matérias:
005-texto-017-triangulos-pitagoricos-inscrito-semicircunferencia
005-texto-018-triangulo-pitagorico3-4-5-inscrito-semicircunferencia
sobre construções de triângulos.
Autor: Ricardo Silva - fevereiro/2017
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Conheça também o novo PASSATEMPO CAÇA-TERNOS
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato