


Assim como os formatos de papeis da série DIN - Deustshe Industrie Normunque (Associação de Engenheiros Alemães) que foram desenvolvidos para uma melhor racionalização de fabricação, mão-obra e uso, as dimensões de telas televisores e de monitores de computadores também o foram, pois se utilizam do Teorema de Pitágoras e é o que veremos no decorrer deste estudo.
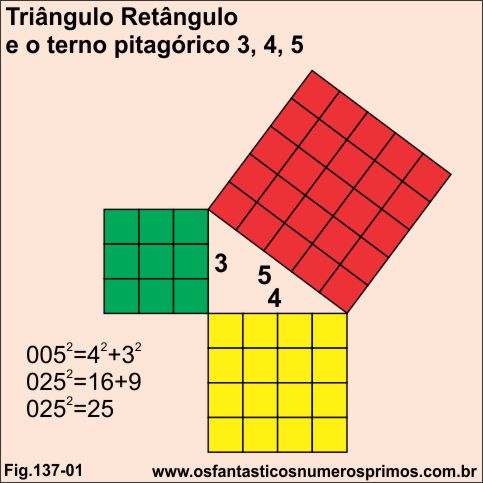
Terno pitagórico é uma sequência de três números inteiros que satisfazem ao Teorema de Pitágoras: a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa (b²+c²=a²), isto é, dois números que elevados ao quadrado e depois somados (b² + c²) tem como resultado um número quadrado perfeito (a²) e que depois de extraído a sua raiz quadrada, o resultado é também um número inteiro.
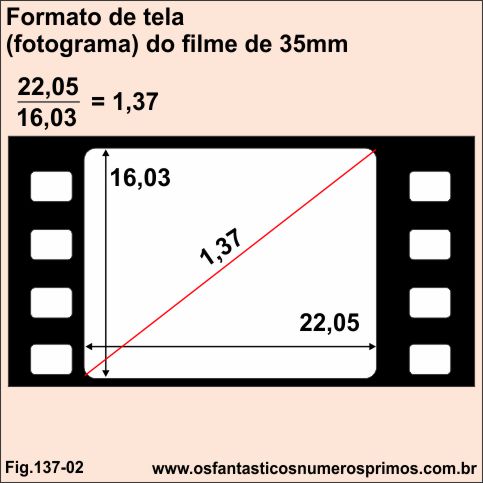
O filme cinematográfico de 35mm tem por pradrão as dimensões da largura: 22,05mm e altura: 16,03mm que correspondem ao fotograma que é área onde a imagem é gravada fotograficamente.
Formato de fotograma é divisão da sua largura: 22,05mm pela sua altura 16,03mm cujo quociente é 1,37.
1, 37 é o Formato das filmagens cinematográficas.

O Formato, o fototograma, a tela e projeção de imagem de televisão é baseado no Teorema de Pitágoras com a utilização do terno pitagórico 3, 4, 5.
Veja alguns cálculos:
4 : 3 = 1, 33 (cateto maior dividido pelo cateto menor)
4 : 3 e 1,33 são chamados de Formatos Full Screen, pois cobrem quase toda a área do fotograma do formato cinematográfico 35mm.
4 : 5 = 0,8 (cateto maior dividido pela hipotenusa)
3 : 5 = 0,6 (cateto menor dividido pela hipotenusa)
Os quocientes (razões): 1,33, 0,8 e 0,6, os quais podemos representá-los por fração, fração irredutível, número decimal ou porcentagem agilizam bastante os cálculos, vejamos:
Exemplo 1)
Em um retângulo cuja diagonal mede 5cm, quais são as medidas dos seus lados?
5 x 0,8 = 4 (medida do lado maior)
5 x 0,6 = 3 (medida do lado menor)
Exemplo 2)
Em uma linha de comprimento ou largura de 4cm (lado maior), desejo construir um retângulo cuja altura seja um número pitagórico, qual é a altura?
4 : 1,33 = 3,00 (medida do lado menor)
O retângulo construído tem as seguintes dimensões, baseado em Ternos Pitagóricos:
comprimento: 4cm (cateto maior)
altura: 3cm (cateo menor)
diagonal: 5cm (hipotenusa)
O formato de tela, a área de visualização de imagem em monitores de computadores, foram baseados no formato de tela de televisão.
Na década de 70, os primeiros computadores eram consoles com teclados, cabos para conexão na entrada de sinal de tv dos televisores, cabos de energia e cabos para conexão em gravadores, pois os programas eram gravados e vendidos em fitas K-7.
Posteriormente, na década de 80, surgiram os Macintoches e Persornal Computers (PCs), computadores os quais eram vendidos com monitor, CPU (gabinete), teclado e mouse, dispositivos separados, mas formando um conjunto.
Os televisores eram fabricados com tecnologia CRT Cathode Ray Tube (CRT) a mesma tecnologia para os monitores de computadores.
A tecnologia CRT perdurou até meados de 2013.
Então na hora em que se comprava e compra computador, os monitores têm como uma de suas características serem vendidos como 14, 15, 17, 19, 20, 21 e 22 polegadas, as mesmas medidas de televisores, medidas estas que se referem a diagonal da área de visualização de imagens, isto é, formato, fotograma, janela, Full Screen, e para ser mais exato: a diagonal do retângulo cujos lados são baseados no Terno Pitagórico Primitivo 3, 4, 5.
Para nós, aqui no Brasil e outros países que tem como hábito e norma fazer medições usando o sistema métrico, na hora em que aparece polegadas e ainda com diagonal..., em um primeiro momento parece complicado, mas com os cálculos matemáticos fica mais fácil.
Exemplo 1)
Monitor cuja diagonal mede 14 polegadas (14 x 2,54cm = 35,56cm), quais são as medidas dos seus lados?
14 x 0,8 = 11,2 (medida do lado maior)
11,2 x 2,54cm = 28,44cm
14 x 0,6 = 8,4 (medida do lado menor)
8,4 x 2,54cm = 21,33cm
As dimensões de um monitor de 14 polegadas são:
largura: 28,5 cm (medidas arredondadas)
altura: 21,5 cm (medidas arredondadas)
| Ternos Pitagóricos derivados da sequência 3, 4 e 5 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1ª | 2ª | 3ª | 4ª | 5ª | 6ª | 7ª | 8ª | 9ª | 10ª | |
| Terno | Ternos | |||||||||
| primitivo | derivados | |||||||||
| cateto menor | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| cateto maior | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| hipotenusa | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
Observe as características desta tabela com ternos pitagóricos:
a) os números da primeira coluna é um terno primitivo pitagórico: 3, 4, 5;
b) o terno da segunda coluna é o dobro da primeira coluna;
c) o terno da terceira coluna é o tripo da primeira coluna e assim por diante;
d) Multiplicando-se o terno primitivo 3, 4, 5 pela sequência de números naturais: 2, 3, 4, 5, 6, 7, 8,... obtêm-se os demais ternos pitagóricos derivados;
e) O terno primitivo 3, 4, 5 são constituídos de números consecutivos e a diferença é de uma unidade entre eles.
f) A diferença entre os números de cada terno derivado é o mesmo número natural que foi muliplicado pelo terno primitivo;
Exemplo 1)
a diferença entre os números do terno (6, 8, 10) é de duas unidades.
Exemplo 2)
a diferença entre os números do terno (9, 12, 15) é de três unidades.
g) São todos números proporcionais e números inteiros:
3 x 8 = 24
4 x 6 = 24
Você então tem um brilhante ideia, vai fabricar monitores e como referência vai usar ternos pitagóricos. Você observou a praticidade que eles proporcionam, aliás o Teorema de Pitágoras é fantástico, assim como toda a Matemática.
Exemplo 3)
Monitor de 10 polegadas (medida da diagonal)
Verificando a tabela - 2ª coluna
Largura: 8 polegadas
Altura: 6 polegadas
Exemplo 4)
Você deseja comprar um monitor de 20 polegadas, e conhecendo o terno pitagórico primitivo 3, 4, 5, faz os cálculos rapidinho:
20 : 5 = 4
4 x 3 = 12 (medida da altura)
4 x 4 = 16 (medida da diagonal)

O formato de tela atual de televisores e monitores de computadores com tecnologias LED, LCD e Plasma é 16:9 (1,77).
x2 = 162 + 92
x2 = 256 + 81
x2 = 337
x = √337
x = 18,35 (diagonal)
Determinando os quocientes (razões):
16 : 9 = 1, 77 (cateto maior dividido pelo cateto menor)
16 : 9 e 1,77 são chamados de Formatos WideScreen.
16 : 18,35 = 0,871 (cateto maior dividido pela diagonal)
9 : 18,35 = 0,490 (cateto menor dividido pela diagonal)
Autor: Ricardo Silva - maio/2017
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato