


Nos dias de hoje, para a fabricação de papel, são utilizados para a obtenção de celulose duas espécies de árvores: o eucalípto e o pinheiro.
Ao longo da história foram utilizados muitos outros tipos materiais para se fabricar papel, os egípcios utilizavam o papiro; os chineses fabricavam papel a partir de fibras vegetais, trapos e bambu; os italianos faziam uso do algodão e linho.
Por volta de 1.450, Gutemberg, após várias experiências, desenvolveu os tipos móveis de metal, com os quais podiam compor textos e livros e posteriormente imprimí-los em prensas com maior rapidez do que textos e livros produzidos por copistas, pois até então, todos os textos e livros eram escritos (copiados) um a um nos mosteiros e conventos.
Esse processo de se produzir texto e livros com maior rapidez deu origem a imprensa e paralelamente com ela o surgimento de oficinas que fabricavam papéis nas mais variadas medidas e tipos, pois até então não se tinha pradronização das medidas de folha de papel.
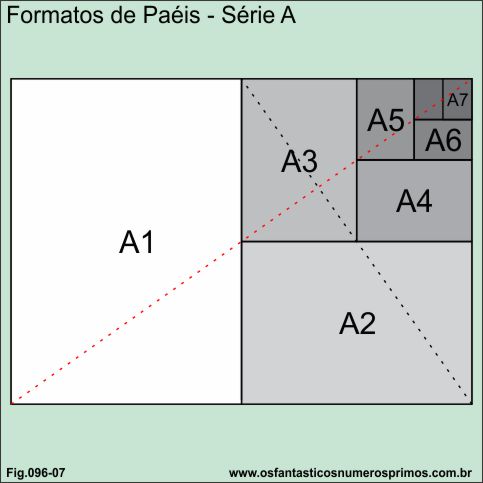
Visando a economia e a racionalização tanto da fabricação e da mão de obra utilizada no setor gráfico, em 1911, a DIN - Deustshe Industrie Normunque (Associação de Engenheiros Alemães) criou um formato padrão de papel, baseado no sistema métrico, o formato "DIN" ou "formato internacional" de papel.
Este formato tem como característica a divisão harmônica da folha de papel, de forma que quando dividida ou dobrada a folha tenha sempre a mesma proporção, isto é, cada formato (folha) é a metade da anterior e o dobro da seguinte.
O que será apresentado a seguir, são demostrações de como o Teorema de Pitágoras foi utilizado para se desenvolver este "Formato Padrão de Papel" e que nós o utilizamos muito no nosso dia-dia o (Formato A4) quando vamos a uma papelaria para comprá-lo, ou quando precisamos tirar uma xerox de um documento em uma Copiadora, ou mesmo quando imprimimos algo em uma impressora de mesa, seja ela uma impressora jato-de-tinta ou laser.
Em qualquer triângulo retângulo, o quadrado da hipotenusa é igual a soma dos quadrados do catetos.
| a² = b² + c² |
Podemos demostrar o teorema, com o famoso triângulo retângulo de lados 3, 4 e 5.
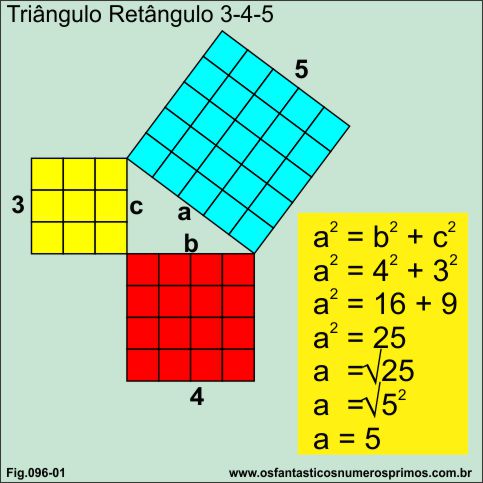
Traça-se uma diagonal entre dois vértices opostos, de forma que obtemos dois triângulos retângulos cujos catetos têm as mesmas medidas.
Aplicando-se o Teorema de Pitágoras, conclui-se que a medida da diagonal de um quadrado é sempre igual ao produto de um lado por √2.
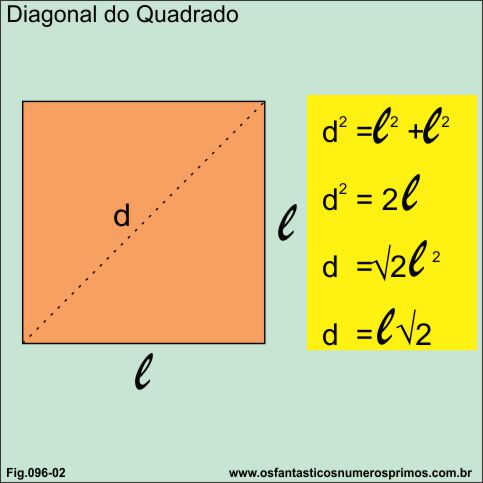
Aplicando o Teorema de Pitágoras em um quadrado cujos lados medem 1, temos a diagonal como resultado o número irracional 1,4142.

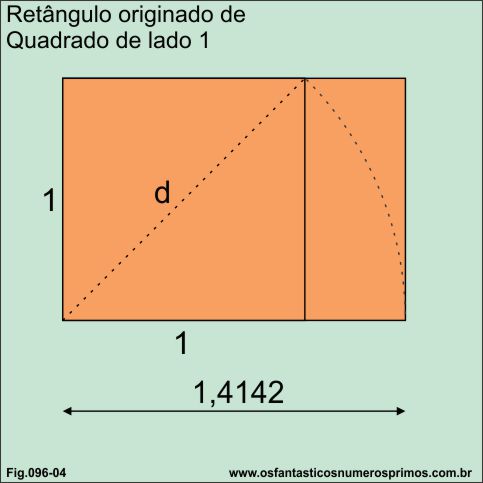
A partir de um quadrado de lado 1, traça-se uma diagonal, com o centro no canto esquerdo inferior, traça-se um arco de circunferência até a base do quadrado e finalmente prolonga-se o lado direito do quadrado formando-se um retângulo.
Este retângulo construído a partir de um quadrado de lado 1, é um retângulo especial, conhecido por: retângulo dinâmico, retângulo de √2, pois através deste retângulo podemos obter outros retângulos menores e proporcionais.
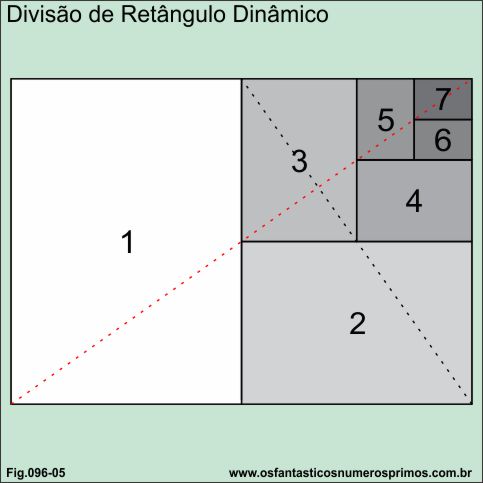
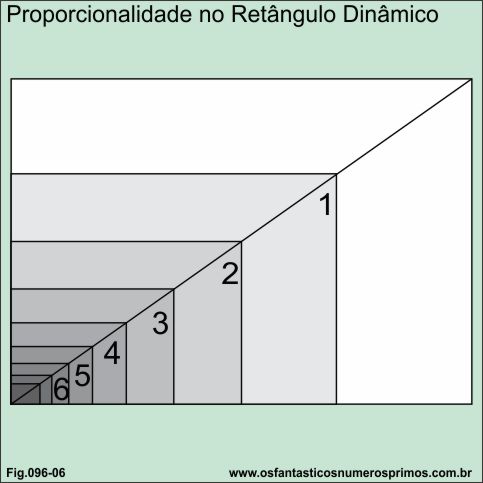
Traçando-se um diagonal e dividindo os retângulos sempre ao meio, obtemos vários outros retângulos menores e proporcionais.
Perceba-que a diagonal (linha vermelha) toca os dois vértices do retângulo maior e do retângulo menor e um dos vértices de cada retângulo menor a partir do retângulo 2.
Estas divisões são infinitas e da mesma forma podemos aumentar o número de retângulos dobrando as medidas de suas larguras e alturas.
Perceba também que cada retângulo dividido a partir do retângulo maior, é a metade do anterior e o dobro do seguinte.
Para provar a proporcionalidade no retângulo dinâmico, sobrepondo cada retângulo menor sobre cada retângulo maior, a diagonal cruza os vértices opostos de cada um dos retângulos.
Fazendo uso da regra de 3 entre dois retângulos, verifica-se que os seus lados são proporcionais um ao outro.
Exemplo:
dimensões do retângulo amarelo: 1 x 1,4142
dimensões do retângulo cinza 1: 0,5 x 0,7071
Aplicando a regra de 3:
| 1 | ___ | 1,4142 |
| 0,5 | ___ | x |
| x | = | 1,4142 . 0,5 |
| __________ | ||
| 1 |
| x | = | 0,7071 |
| __________ | ||
| 1 |
| x | = | 0,7071 |
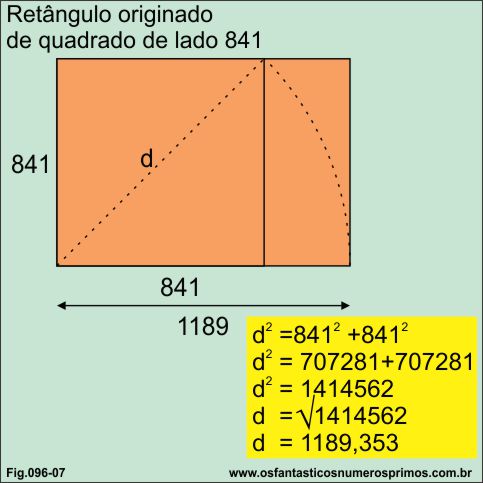
Aplicando o Teorema de Pitágoras em um quadrado de lado 841, temos como resultado a medida da diagonal: 1189
Traçando-se um diagonal e dividindo os retângulos sempre ao meio, obtemos vários outros retângulos menores e proporcionais.
Autor: Ricardo Silva - novembro/2014
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato