capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Ternos pitagóricos e Equação do 2º grau - 132

Terno pitagórico é uma sequência de 3 números inteiros que elevados cada um ao quadrado satisfazem ao Teorema de Pitágoras.

A partir do terno pitagórico primitivo 3, 4 e 5, podemos formar infinitos ternos pitagóricos derivados utilizando fórmulas específicas, Equação do Segundo Grau, como no interessante exemplo a seguir e também através de algumas técnicas e artifícios, simplesmente, escolhendo-se quaisquer números múltiplos de 3, de 4 ou de 5.

Triângulo retângulo cujos lados são números pares consecutivos

Veja este interessante problema algébrico extraído do livro Tudo é Matemática - 9º ano - Edição de 2011 - do Professor Luiz Roberto Dante - Editora Ática - Capítulo 3 - página 65 - exercício 51, aqui resolvido por meio de equação do 2º grau com o método de Completamento de Quadrado.

"Em um triângulo retângulo as medidas dos seus três lados, em centimetros, são números consecutivos. Use a relação de Pitágoras e descubra quais são essas medidas."

terno pitagórico 6, 8 e 10 e equação do segundo grau

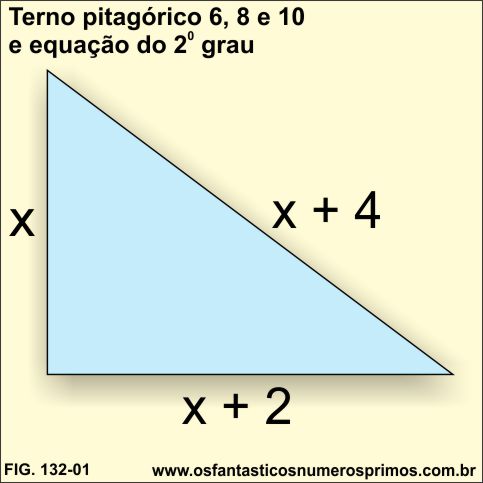
a) termos:

x+2

x+4

b) Montagem e resolução da equação:

(x+4)² = x² + (x+2)²

x² + 8x + 16 = x² + x² + 4x + 4

x² + 8x + 16 = 2x² + 4x + 4

x² - 2x² + 8x - 4x + 16 - 4 =

-x² + 4x + 12 = 0 (multiplicando por -1)

x² - 4x - 12 = 0

x² - 4x = + 12

x² - 4x + 4 = + 12 + 4 (completando o quadrado)

(x - 2)² = + 12 + 4 (fatorando o primeiro membro)

(x - 2)² = + 16

x - 2 = ± √ 16

x - 2 = ± 4

x' = + 4 + 2 = 6

x" = - 4 + 2 = -2 (não serve)

c) Resultado

x = 6

x + 2 =

= 6 + 2 = 8

x + 4 =

= 6 + 4 = 10

As medidas dos lados do triângulo retângulo são os pares consecutivos: 6, 8, 10.

6 = cateto menor

8 = cateto maior

10 = hipotenusa

Ternos pitagóricos primitivos e derivados

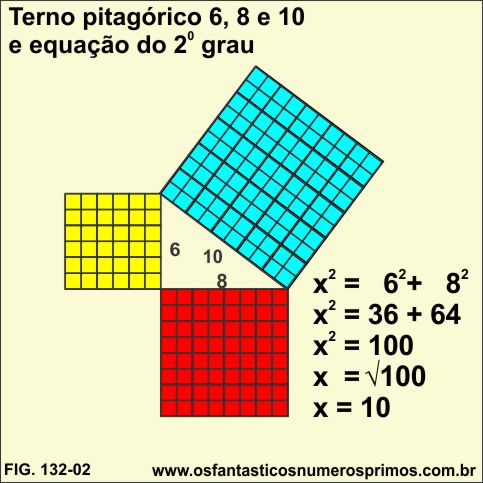
As medidas dos lados do triângulo retângulo do exercício acima é um terno pitagórico derivado de um triângulo retângulo 3, 4 e 5.

Analisemos a tabela:

Ternos Pitagóricos derivados da sequência 3, 4 e 5

	Terno	Ternos
	Primitivo	Derivados

	1ª	2ª	3ª	4ª	5ª	6ª	7ª	8ª	9ª	10ª

cateto menor	3	6	9	12	15	18	21	24	27	30

cateto maior	4	8	12	16	20	24	28	32	36	40

hipotenusa	5	10	15	20	25	30	35	40	45	50

www.osfantasticosnumerosprimos.com.br

Na 1ª coluna, a sequência que aparece é 3, 4 e 5, com estes valores podemos desenhar um triângulo retângulo de lados 3, 4 e 5.

Por ser a primeira sequência da tabela é chamado de terno pitagórico primitivo.

As demais sequências são múltiplos de cada termo do terno primitivo.

A partir da 2ª coluna, as demais sequências são chamadas de ternos pitagóricos derivados, pois derivam da sequência da 1ª coluna.

Características nos ternos pitagóricos derivados de 3, 4 e 5

Algumas características se destacam nos ternos pitagóricos derivados da sequência 3, 4 e 5:

a) 1ª coluna, tem-se 3 números concecutivos: 3, 4 e 5 formando um terno pitagórico, esta sequência forma o menor triângulo retângulo de números inteiros;

observação: a diferença entre cada termo é de 1 unidade.

b) 2ª coluna, o terno pitagórico 6, 8 e 10 é formados por pares consecutivos e se destaca entre os demais ternos derivados;

observação: a diferença entre cada termo é de 2 unidades.

c) nas colunas ímpares, os ternos pitagóricos são formados por dois números ímpares e um número par;

d) nas colunas pares, os ternos pitagóricos são formados por três números pares.

e) em cada coluna, a diferença entre cada termo de uma sequência de um terno pitagórico é o mesmo número da sequência da coluna.

exemplos:

na primeira coluna, uma unidade é a diferença entre os termos do terno 3, 4 e 5;

na segunda coluna, duas unidades é a diferenças entre os termos do terno 6, 8 e 10;

na terceira coluna, três unidades é a diferença entre os termos do terno 9, 12 e 15.

Gerando ternos pitagóricos a partir do terno 3, 4 e 5

Os números da sequência 3, 4 e 5 são fáceis de se lembrar, de se recitar e de se escreverem, pois podemos fazer contas utilizando-se dos dedos das mãos ou fazendo cálculos mentalmente, etc.

A partir do terno pitagórico primitivo 3, 4 e 5, escolhendo-se um número qualquer como fator e multiplicando por cada um dos termos do terno, podemos formar um novo terno pitagórico.

Exemplo 1)

3 x 3 = 9

4 x 3 = 12

5 x 3 = 15

9, 12 e 15 é um terno pitagórico derivado da sequência 3, 4 e 5.

A partir de qualquer múltiplo de um dos termos do terno 3, 4, 5, pode-se formar um novo terno pitagórico.

Exemplo 2)

27 é um múltiplo de 3, pois:

27 : 3 = 9

3 x 9 = 27

4 x 9 = 36

5 x 9 = 45

27, 36 e 45 é um terno pitagórico derivado da sequência 3, 4 e 5

observação: a diferença entre os termos do terno pitagórico é de 9 unidades.

Exemplo 3)

44 é múltiplo de 4, pois:

44 : 4 = 11

3 x 11 = 33

4 x 11 = 44

5 x 11 = 55

observação: a diferença entre os termos do terno pitagórico é de 11 unidades.

Conclusão

A partir deste exemplo de exercício extraído de livro didático, percebemos o quão é maravilhosa e instigante a Matemática, através do conceito de números consecutivos e equação de 2º grau, pôde-se determinar três números (desconhecidos) que se relacionam a um dos teoremas mais importantes, que é o Teorema de Pitágoras.

Interessante notar também é que a partir de uma sequência inicial (terno primitivo 3, 4 e 5) consegue-se formar outras sequências de ternos, simplesmente, duplicando, triplicando, quadruplicando,...etc. cada um dos termos do terno primitivo simultaneamente ou escolhendo-se um número qualquer e multiplicando-o por cada um dos termos do terno primitivo.