Página de estudos de matemática e sequências numéricas

Ternos pitagóricos - 069

Terno pitagórico é uma sequência de três números inteiros que satisfazem ao Teorema de Pitágoras: A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa (b² + c² = a²), isto é, dois números que elevados ao quadrado e depois somados (b² + c²) tem como resultado um número quadrado perfeito (a²) e que depois de extraído a sua raiz quadrada, o resultado é também um número inteiro.

Neste estudo, elevou-se ao quadrado os primeiros 5.000 números naturais e posteriormente somou-os de dois em dois, obtendo 5 ternos pitagóricos com ocorrências aleatórias os quais são apresentados a seguir.

Terno pitagórico primitivo 3, 4, 5

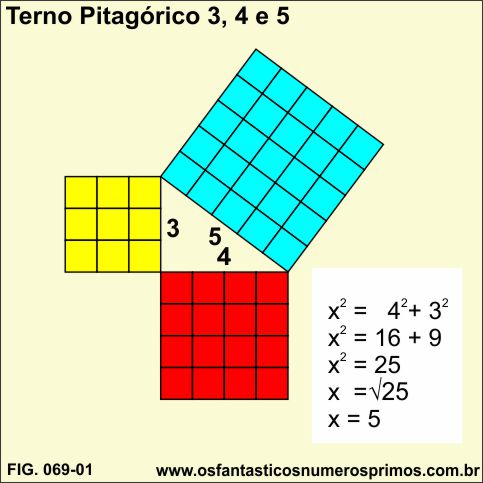
O clássico terno pitagórico 3, 4 e 5 tem um quê de especial:

a) é um terno pitagórico primitivo, pois a partir dele, podemos gerar ternos pitagóricos derivados, simplesmente multiplicando os seus termos pela sequência dos números naturais: 1, 2, 3, 4, 5,...

exemplo a)

3 x 2 = 6

4 x 2 = 8

5 x 2 = 10

6, 8, 10

exemplo b)

3 x 3 = 9

4 x 3 = 12

5 x 3 = 15

9, 12, 15

exemplo c)

3 x 4 = 12

4 x 4 = 16

5 x 4 = 20

12, 16, 20

b) é uma sequência de três números consecutivos e entre eles dois números primos;

3 e 5 são números primos.

c) 3, 4 e 5 é o primeiro terno pitagórico primitivo;

d) 4 é a média aritmética dos três termos;

3 + 4 + 5 = 12

12 : 3 = 4

e) 5 subtraído de 12 é igual a soma dos dois primeiros termos da sequência;

12 - 5 = 7

3 + 4 = 7

f) 4 subtraído de 12 é igual a soma dos dois termos extremos da sequência;

12 - 4 = 8

3 + 5 = 8

g) 3 subtraído de 12 é igual a soma do segundo e terceiro termos da sequência;

12 - 3= 9

4 + 5 = 9

Ternos pitagóricos primitivos

Ternos pitagóricos primitivos são ternos gerados a partir de dois número primos entre si e que podem gerar ternos pitagóricos derivados.

Este método e outros para se obterem ternos pitagóricos se encontram no Livro Digital Ternos Pitagóricos e Sequências Numericas que demonstra que determinados ternos pitagóricos primitivos formados pela sequência: ímpar-par-ímpar estão estritamente relacionados com a sequência de números triangulares e a sequência de números ímpares, isto é, para cada ordem / posição de um número triangular há um terno pitagórico primitivo; e que também de cada número ímpar pode-se formar um terno pitagórico com o seu respectivo número quadrado perfeito ímpar.

Excetuando-se o terno pitagórico primitivo 3 - 4 - 5 que é o único terno pitagórico formado por 3 números consecutivos, os demais ternos foram nomeados de TERNOS PRIMITIVOS RAROS pois são formados por dois primeiros termos consecutivos e suas ocorrências são raras e aleatórias semelhante a sequência de números primos.

Interessante observar que os ternos pitagóricos gerados são da seguinte forma: ímpar-par-ímpar e par-ímpar-par, sendo que os primeiro e segundo termos são números consecutivos.

A partir de uma tabela, como no exemplo abaixo, na coluna NÚMEROS, foram inseridos os números naturais, na coluna QUADRADOS, os respectivos quadrados perfeitos de cada número natural.

Na coluna SOMA DE 2 QUADRADOS obteve-se a soma de 2 números quadrados pefeitos da seguinte forma:

exemplo a)

O resultado 25 é soma dos quadrados 9 + 16

A raiz quadrada de 25 é 5

exemplo b)

O resultado 841 é a soma dos quadrados 400 + 441

A raiz quadrada de 841 é 29

Ternos pitagóricos primitivos raros

São ternos pitagóricos que possuem dois termos consecutivos.

Terno pitagórico 3, 4 e 5

O primeiro terno pitagórico a aparecer na tabela é 3, 4 e 5, este terno por excelência é o único terno formado por três números consecutivos.

Terno pitagórico 20, 21 e 29

Segundo terno pitagórico raro a aparecer é 20, 21 e 29.

A raiz quadrada de 841 é 29.

20 e 21 são números consecutivos.

Terno pitagórico 119, 120 e 169

Terceiro terno pitagórico raro a aparecer 119, 120 e 169.

A raiz quadrada de 28.561 é 169.

119 e 120 são números consecutivos.

Terno pitagórico 696, 697 e 985

Quarto terno pitagórico raro a aparecer 696, 697 e 985.

A raiz quadrada de 970.225 é 985.

696 e 697 são números consecutivos.

Terno pitagórico 4059, 4060 e 5741

Quinto terno pitagórico primitivo raro 4059, 4060 e 5741.

A raiz quadrada de 32.959.081 é 5741.

4059 e 4060 são números consecutivos.

Autor: Ricardo Silva - janeiro/2017

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-070-ternos-pitagoricos-angulos-triangulos-retangulos

011-estudos-098-soma-dois-numeros-quadrados-perfeitos-consecutivos

011-estudos-132-equacao-segundo-grau-ternos-pitagoricos

011-estudos-133-ternos-pitagoricos-sequencias-numericas

Conheça também o novo PASSATEMPO CAÇA-TERNOS

006-passatempo-caca-ternos

Livro Ternos Pitagóricos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

L A N Ç A M E N T O ! ! !

NOVO LIVRO DIGITAL:

DESCOBRINDO NÚMEROS PRIMOS A PARTIR DE NÚMEROS COMPOSTOS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.