


Todo polígono regular pode ser inscrito em uma circunferência.
Imagine a seguinte situação, deseja-se projetar um eixo de uma roda cuja circunferência tem 5 cm de diâmetro. Se o eixo for em formato cilíndrico, não há mistério algum, pois terá a mesma medida do diâmetro, mas se o eixo for em formato de um prisma quadrangular, qual será as medidas dos lados?
Há cálculos rápidos para se determinar os lados de um quadrado inscrito e circunscrito em uma circunferência, mas antes vamos ver as relações existentes entre a circunferência e o quadrado através de construções geométricas e cálculos matemáticos.
Desenhando circunferências de dimensões quaisquer e posteriormente traçando-se dois diâmetros perpendiculares em forma de "xis", os pontos em que as linhas dos diâmetros tocam a circunferência determinam as medidas dos lados do quadrado.
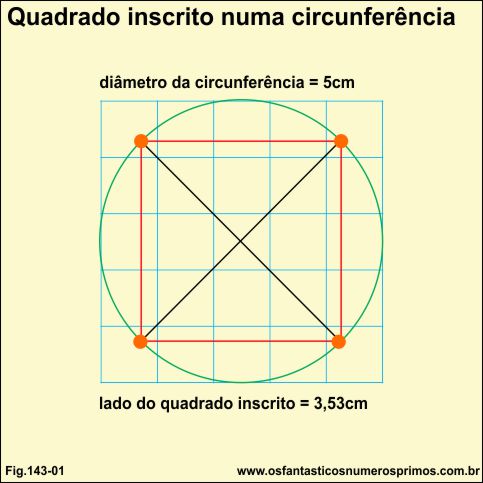
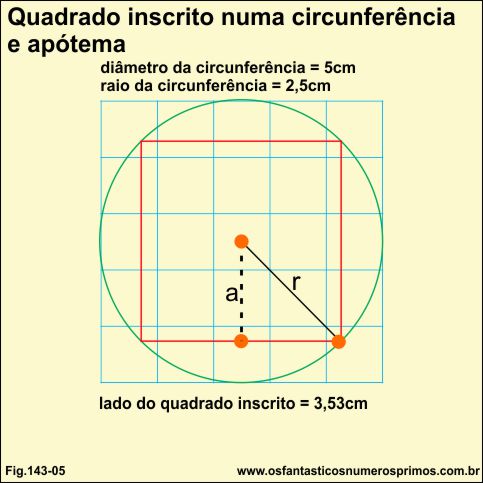
No exemplo acima, a circunferência está desenhada em diagrama quadriculado de 1cm cada.
A circunferência possui um diâmetro de 5 cm e os lados do quadrado tem 3,53 cm.
Traçando-se dois diâmetros perpendiculares e posteriormente o quadrado, determinamos também 2 triângulos retângulos isóceles maiores e 4 menores, com os quais podemos utilizar o Teorema de Pitágoras e descobrir as medidas dos lados do quadrado em função do diâmetro.
Observação importante: no quadrado inscrito numa circunferência o diâmetro é também a diagonal do quadrado.
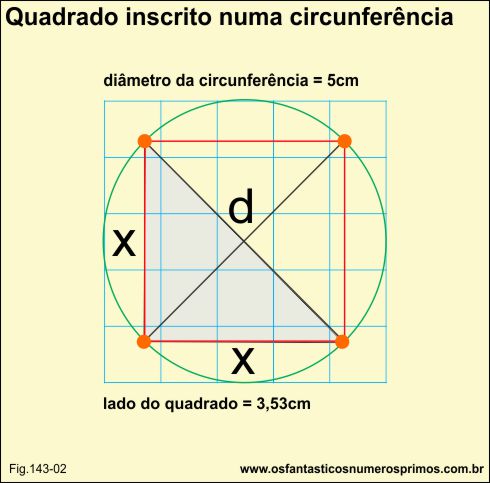
d2 = x2 + x2
52 = x2 + x2
25 = 2x2
25/2 = x2
12,5 = x2
√12,5 = x
x = 3,53
Traçando-se os diâmetros perpenciculares em formato de "xis" e posteriormente o quadrado, determinamos também quatro triângulos retângulos isóceles menores, com os quais podemos utilizar o Teorema de Pitágoras e determinar as medidas dos lados do quadrado em função do raio da circunferência.
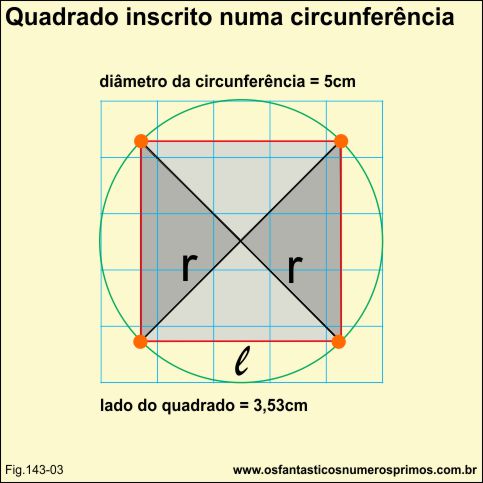
L2 = r2 + r2
L2 = 2,52 +2,52
L2 = 6,25 + 6,25
L2 = 12,5
L = √12,5
L = 3,53
Outro método de se determinar a medida dos lados do quadrado inscrito num circunferência é dividindo a medida do diâmetro pela raiz quadrada de 2 (√2 ).
5 : √2 =
= 5 : 1,4142
= 3,5355
Outra relação interessante existente entre circunferência e quadrado é que a partir do produto do diâmetro pela raiz quadrada de dois (√2 ) determina-se um outro quadrado, só que este circunscrito a circunferência.
Observação importante:
a) no quadrado inscrito numa circunferência o diâmetro é também a diagonal do quadrado.
b) no quadrado circunscrito numa circunferência o diâmetro é também o lado do quadrado.
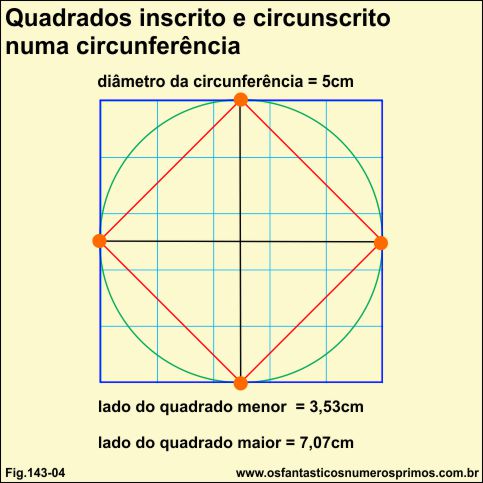
5 x √2 =
= 5 x 1,4142
= 7,0710
Apótema é o seguimento de reta que parte do ponto médio do lado de um polígono até o centro da circunferência e do polígono.
Tendo-se uma das medidas (raio, lado ou apótema), podemos encontrar as duas outras. Nos cálculos podemos utilizar as relações métricas e trigonométricas nos triângulos retângulos.
apótema = metade do lado quadrado
a = 1/2 x L
a = 1/2 x 3,53
a = 1,765
raio = metade da diagonal
r = 1/2 x d
r = 1/2 x (3,53 √2)
r = 1,765 √2
r = 1,765 x 1,4142..
r = 2,496...(aproximadamente)
Exemplo:
Numa circunferência de 6cm de diâmetro calcular o apótema utilizando o Teorema de Pitágoras.
r2 = L2 + L2
32 = L2 + L2
32 = 2 L2
9 = 2 L2
9/2 = L2
L2 = √4,5
L = 2,12
Verificação:
Diâmento : √2 = lado do quadrado inscrito
6 : √2 = 4,24....
1/2 do lado do quadrado = apótema
1/2 x 4,24 = 2,12
ou
1/2 do diâmetro (raio) : √2 = apótema
3 : √2 = 2,12...
Autor: Ricardo Silva - julho/2017
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato