


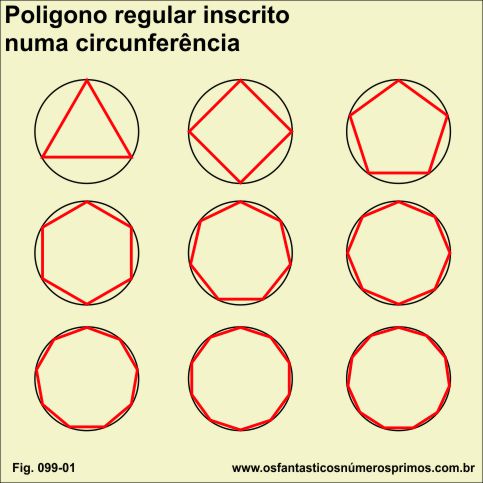
Observe os polígonos regulares inscritos numa circunferência, a medida que os números de lados dos polígonos regulares aumentam, eles tendem a chegar a forma da própria cincunferência.(figura 1)
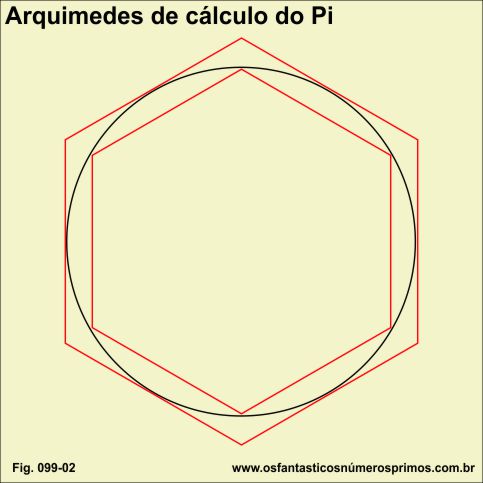
O matemático grego Arquimedes (287-212 a.C) desenvolveu um método de se chegar a aproximação do número (pi) 3,1415... através de polígonos regulares inscritos e circunscritos.
Por meio dos perímetros de polígonos regulares inscritos e circunscritos, Arquimedes chegou a valores próximos do comprimento da circunferência e que dividindo pelo dobro do raio (2r) esses resultados também se aproximavam ao número (pi) 3,1415... (figura 2)
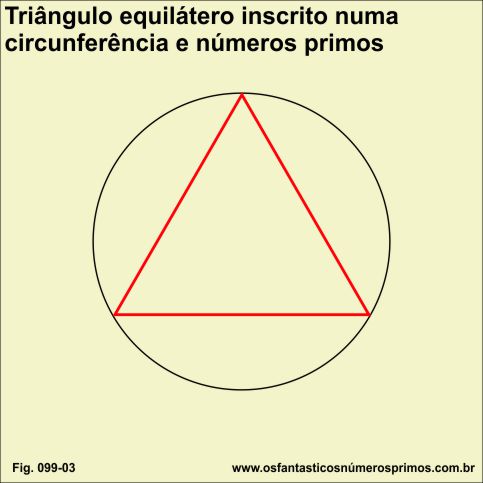
Replicando-se em determinado ângulo fixo um triângulo equilátero inscrito numa circunferência, as réplicas originadas são em quantidades ímpares cujos números são primos.
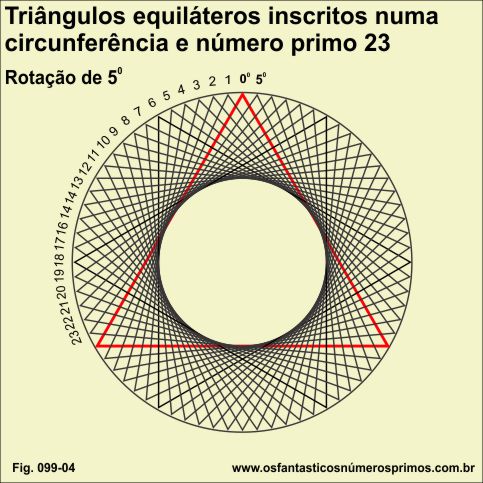
Replicando e rotacionando um triângulo equilátero em ângulo de 5 graus, inscrito numa circunferência, obtem-se 23 réplicas.
23 é um número primo.
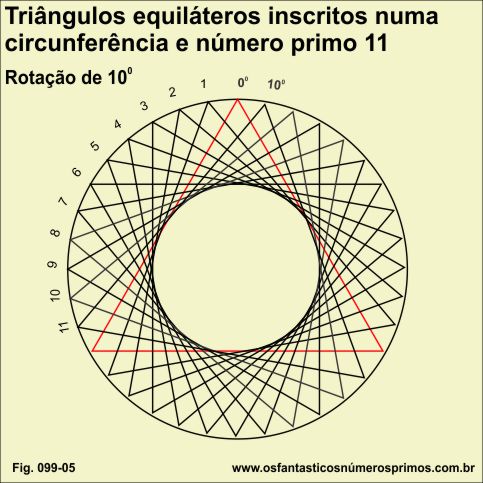
Replicando e rotacionando um triângulo equilátero em ângulo de 10 graus, inscrito numa circunferência, obtem-se 11 réplicas.
11 é um número primo.
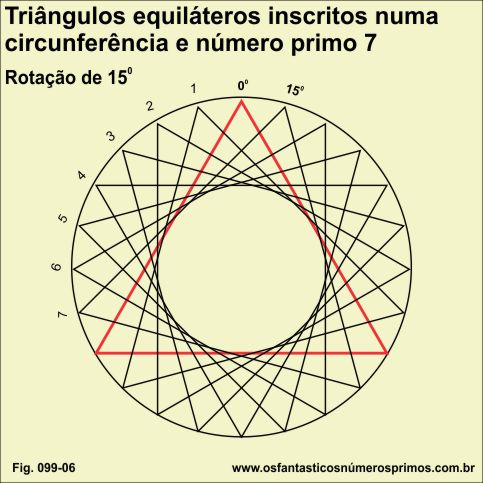
Replicando e rotacionando um triângulo equilátero em ângulo de 15 graus, inscrito numa circunferência, obtem-se 7 réplicas.
7 é um número primo.
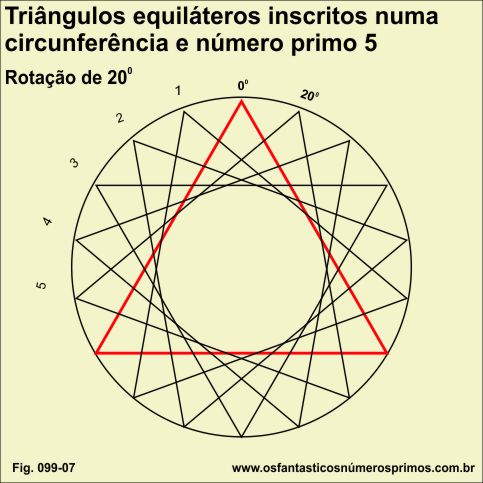
Replicando e rotacionando um triângulo equilátero em ângulo de 20 graus, inscrito numa circunferência, obtem-se 5 réplicas.
5 é um número primo.
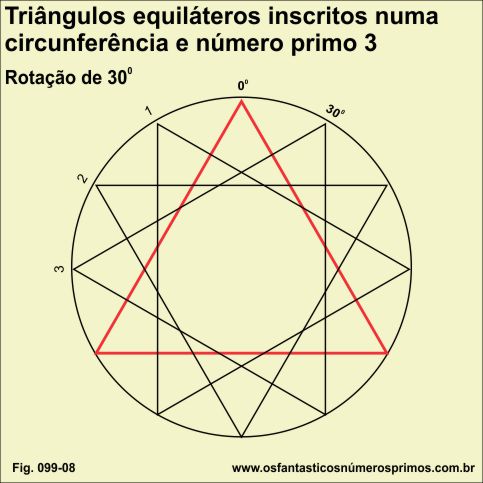
Replicando e rotacionando um triângulo equilátero em ângulo de 30 graus, inscrito numa circunferência, obtem-se 3 réplicas.
3 é um númeos primo.
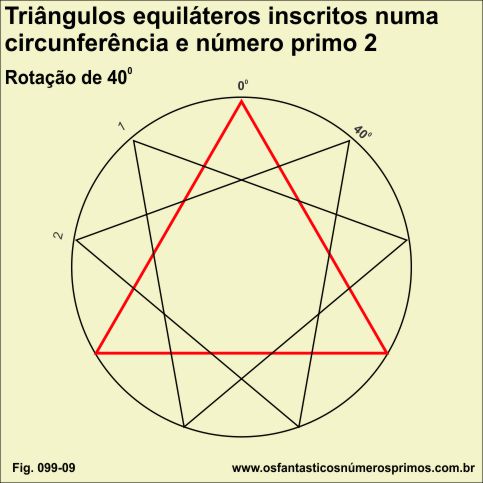
Replicando e rotacionando um triângulo equilátero em ângulo de 40 graus, inscrito numa circunferência, obtem-se 2 réplicas.
2 é um número primo.
Autor: Ricardo Silva
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato