


Por meio de arranjos de pontos podem ser construídos figuras geométricas diversas, como triângulos, quadrados, pentágonos, etc...
Neste estudo são utilizados figuras geométricas de triângulos equiláteros para formarem também figuras geométricas de triângulos equiláteros e hexágonos, os quais apresentam interessantes formações de sequências numéricas.
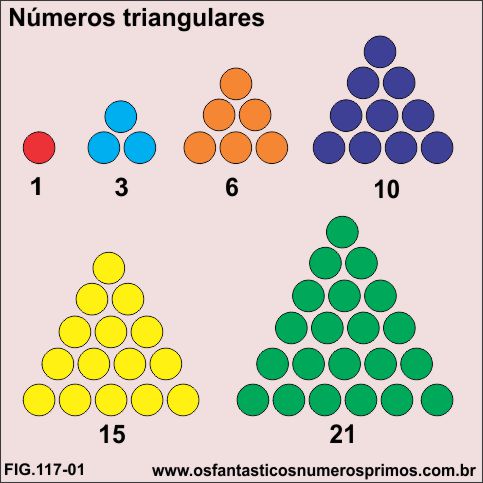
Podem-se obter números triângulares das seguintes formas:
a) por meio da soma consecutiva de números naturais:
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
e assim sucessivamente...
b) por meio de arrajos de pontos formando figuras de triângulos equiláteros:
Exemplo1)
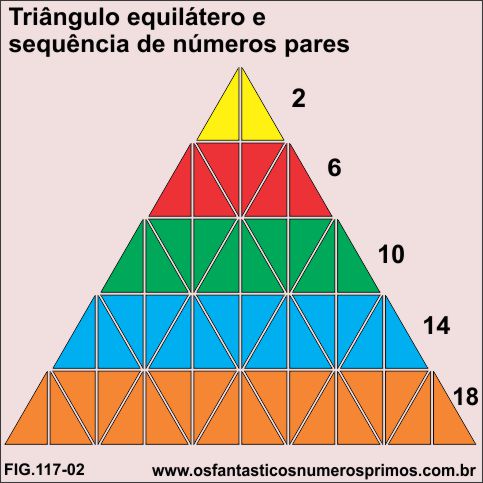
Desenhando-se dois triângulos retângulos com 30, 60 e 90 graus, de forma que os catetos menores fiquem como base e encostando-se os catetos maiores, consegue-se se formar um triângulo equilátero (amarelo) como no exemplo da figura 117-02.
Replicando-se vários triângulos retângulos e os colocando na base do triângulo equilátero (amarelo), a altura aumenta a cada fileira acrescentada.
Na primeira fileira (topo) temos 2 triângulos retângulos amarelo que formam 1 triângulo equilátero.
Na segunda fileira (base) temos 6 triângulos retângulos vermelho que formam 3 triângulos equiláteros.
A cada linha acrescentada na base e somando-se sempre 4 triângulos retângulos as quatidades de triângulos retângulos anteriores, obtem-se a seguinte sequência númerica de números pares: 2, 6, 10, 14, 18, 22, 26, ... de razão 4.
2
2 + 4 = 6
6 + 4 = 10
10 + 4 = 14
14 + 4 = 18
e assim sucessivamente...
Exemplo 2)
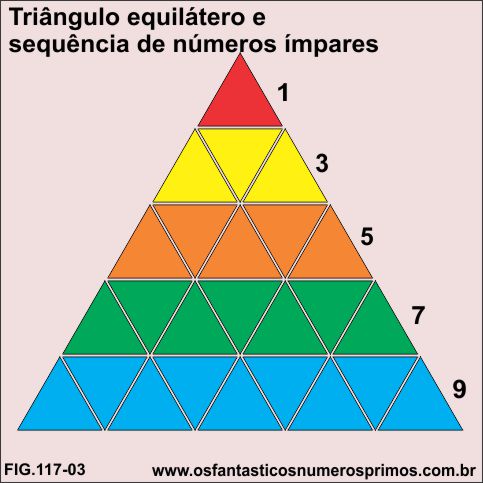
A partir de triângulos equiláteros replicados e acrescentando os a base de outros triângulos equiláteros, aumentam-se suas alturas e consequentemente os seus lados.
Acrescentado-se sempre 2 triângulos equiláteros a partir do triângulo equilátero vermelho, obtemos a sequência de números ímpares: 1, 3, 5, 7, 9 , ...
1
1 + 2 = 3
3 + 2 = 5
5 + 2 = 7
7 + 2 = 9
e assim sucessivamente...
Somando-se as quantidades de triângulos equiláteros de cada linha consecutivamente, obtem-se a sequência de números quadrados perfeitos:
1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
Autor: Ricardo Silva - abril/2016
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato