


Através de alguns métodos são possíveis de se fazerem construções geométricas nas quais podemos inscrever triângulo em um quadrado.
Neste estudo são apresentados interessantes técnicas com as quais se podem contruir Quebra-cabeças semelhantes ao Tangran e construir triângulo equilátero e isóceles de mesma área de um quadrado.
No livro Design e Comunicação Visual, autor Bruno Munari, Editora Martins Fontes, edição de 2001, página 139, há um diagrama de um quadrado que dividindo-o em 4 partes e posteriormente rotacionando e montando estas partes, forma-se a figura de um triângulo que no livro diz ser um triângulo equilátero.
A divisão do quadrado mostrado no livro lembra o quebra-cabeça japonês TANGRAN, um quadrado dividido em 7 partes com as quais são possíveis de se montarem milhares de figuras de animais, objetos, números, letras, etc.
Foi feito o diagrama mostrado no livro, utilizando papel milimetrado conforme a figura 1, só que quando montado, o triângulo resultante é um triângulo isóceles e não um triângulo equilátero.
No exemplo abaixo, os pontos E, F, G e H são os pontos médios de cada lado do quadrado e o ponto I é o ponto médio do seguimento EF.
Em um triângulo isóceles há dois lados com medidas iguais e um lado com medida diferente.
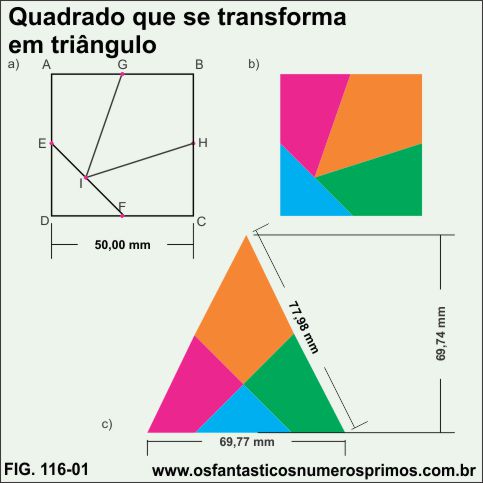
Não ficando satisfeito, fiz e ainda continuo fazendo nos tempos vagos, outros quadrados com outras divisões para tentar montar um triângulo equilátero com a mesma área de um quadrado, não deixa de ser um desafio para fazer os neurônios se eletrizarem.
Tudo isto, fez me lembrar de um dos grandes problemas matemático e geométrico: A quadratura do círculo, que consiste em construir uma região quadrada que tenha a mesma área de um círculo dado.
A partir de um quadrado, com centro em C e abertura em D, faça um arco; com a mesma abertura, centro em D, faça o segundo o arco e marque o ponto E. Una os pontos C, D e E, formando-se assim um triângulo equilátero.
Nesta construção, obtem-se dois triângulos equiláteros: o amarelo e o azul e sobra uma parte vermelha.
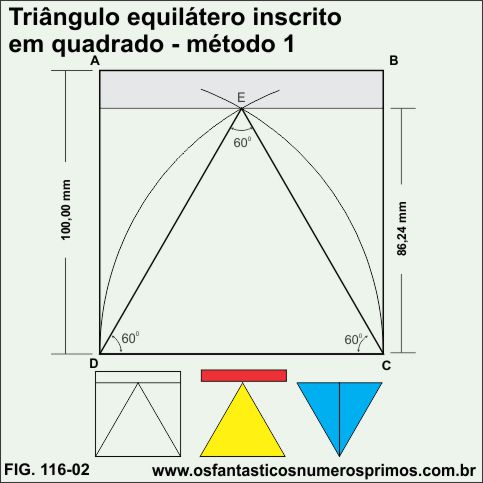
A partir do ponto D do quadrado, com o transferidor ou com uso de compasso marca-se 15 graus a partir da base e faça um seguimento até a lateral direita, marcando o ponto F; marque 15 graus a partir da lateral esquerda do quadrado e faça o segundo seguimento até o topo do quadrado, marcando o ponto E. Tem-se um triângulo equilátero DEF.
Nesta construção também, obtêm-se dois triângulos equiláteros: o amarelo e o azul e sobra uma parte vermelha.
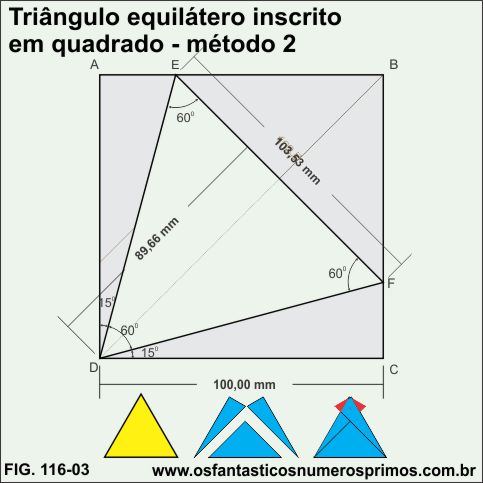
Neste exemplo de construção, têm-se triângulos equiláteros: sendo um principal em amarelo e um segundo em azul divididos em "gomos" de triângulos retângulos de 30, 60 e 90 graus de mesma largura e altura e um terceiro em vermelho, menor, construído com fatias da parte que sobra do quadrado.
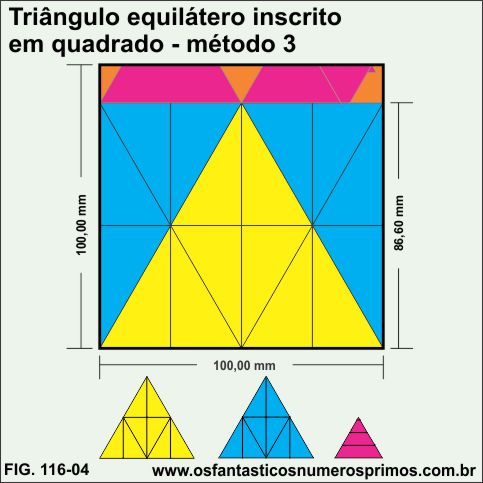
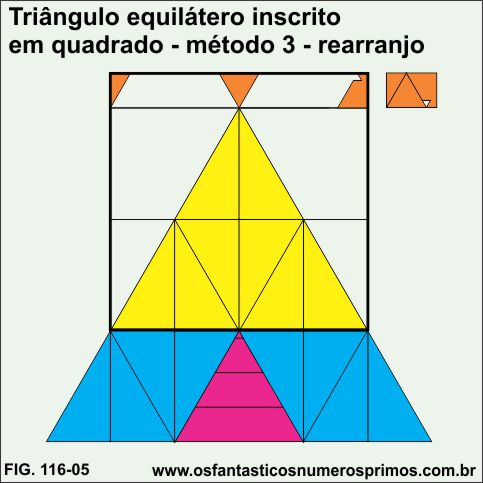
Com a mesma construção geométrica da figura 4, pode-se fazer um novo remanejamento dos "gomos" de triângulos retângulos e aumentar o triângulo equilátero a partir de sua base, ficando este com sua altura maior.
Interessante obsevar nesta disposição é que o retângulo que sobra no topo do quadrado é possível montar um triângulo equilátero vermelho para se finalizar o encaixe do triângulo equilátero maior.
As partes laranja são as que sobram do retângulo do topo do quadrado.
Veja outra forma de construção geométrica publicada no WebSite do Professor Marco Manetta:
Site: www.dinamatica.com.br
http://www.dinamatica.com.br/2011/11/triangulo-equilatero-inscrito-no.html
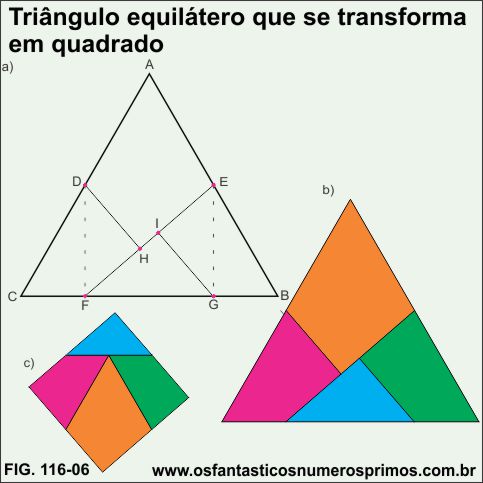
Veja a construção geométrica de dividir um triângulo equilátero em 4 partes e posteriormente montar um quadrado de mesma área do matemático inglês Henry Ernest Dudeney (10 April 1857 - 23 April 1930) no WebSite do Professor Marco Manetta.
WebSite: www.dinamatica.com.br
a) marque o ponto médio D de AC e E de AB;
b) projete o ponto médio D em BC (linha pontilhada) e marque o ponto F;
c) projete o ponto médio E em BC (linha pontilhada) e marque o ponto G;
d) faça o seguimento EF;
e) faça um seguimento perpendicular em EF a partir de D e marque o ponto H;
f) faça outro seguimento perpendicular em EF a partir de G e marque o ponto I;
Exemplo extraído do livro: Problemas de Desenho Linear Geométrico - Coleção Manuais Técnicos LEP - Editora LEP S.A. - 8a. edição - 1960 - pág. 81.
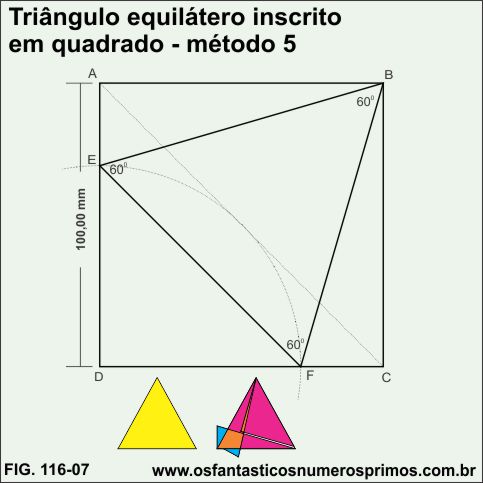
a) desenha-se um quadrado ABCD;
b) centro em D, traça-se um arco com abertura até a diagonal;
c) marca-se os pontos E no lado esquerdo e F na base do quadrado;
d) unindo-se os pontos BEF, tem-se um triângulo equilátero. Nesta construção também, obtêm-se dois triângulos equiláteros: o amarelo e o magenta e sobram as partes azul e as aréas de sobreposições laranja.
Querendo participar deste desafio, mande um link ou um outro modelo diferente de construção de triângulo equilátero inscrito em um quadrado.
Autor: Ricardo Silva - abril/2016
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato