


O quadrado como os demais polígonos regulares são auto replicáveis, isto é, a partir de lados com medidas unitárias, podemos obter outros quadrados ou outros polígonos com medidas proporcionais.
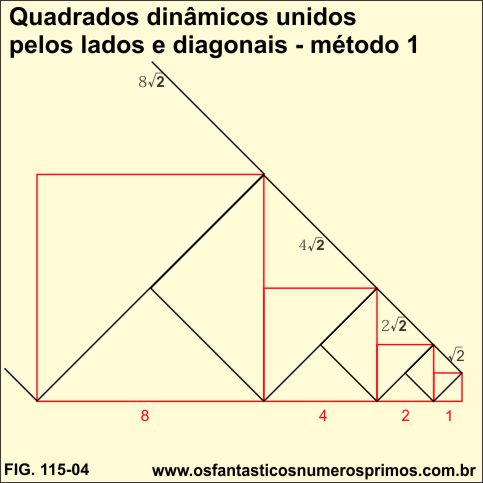
Os quadrados dinâmicos são uma sequência de quadrados obtidos a partir de um quadrado de lados unitários e que podem ser replicados proporcionalmente por meio do ponto médio dos seus lados, pelas suas diagonais ou pelos seus lados.
Faça de conta que você nunca ouviu falar do TEOREMA DE PITÁGORAS: a²= b²+c².
Ai, você precisa desenhar um quadrado cujos lados devem ter 1cm.
Você pega papel (de preferência, papel milimetrado), lápis e régua para desenhar um quadrado perfeito cujos lados devem ter 1cm.
Depois você precisa medir diagonal do quadrado que você desenhou, pega a régua e a inclina para melhor medir a diagonal...
A régua marca 1,4 cm, você ajusta a régua e vê 1,45cm, ajusta novamente e vê 1,5cm, você pensa, pensa e diz para você mesmo, qual é a medida certa?
Realmente não tem um medida certa, isto é, uma medida exata, mas o que você vê na régua são medidas aproximadas.
Você não fica satisfeito e começa a desenhar outros quadrados com outras medidas com lados maiores e constata que as medidas das diagonais também acontecem o mesmo, não é possível obter medida exata.
Então, fazendo o uso do TEOREMA DE PITÁGORAS e de uma calculadora, você constata que a medida da diagonal do quadrado de lado 1 é √ 2 , aproximadamente 1,414213562373095..., a diagonal do quadrado de lado 2 é 2√, aproximadamente 2,82842712474619..., todos números irracionais.
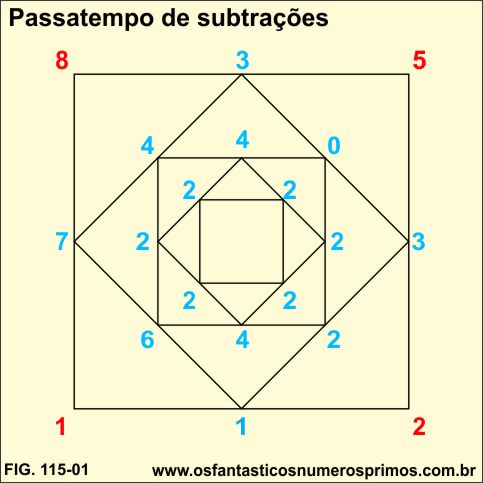
a) Escreva quatro números quaisquer nos vétices de um quadrado (números em vermelho)
b) Subtraia os números entre cada vértice e o coloque no ponto médio dos lados do quadrado o resultado.
c) Continue subtraindo os números entre cada vértice e colocando o resultado no ponto médio dos lados do quadrado até que todas as diferenças sejam iguais.
Este Passatempo se encontra na Coleção Tudo é Matemática, 7 ano , página 189, do Professor Luiz Robeto Dante, editado pela Editora Ática, edição 2011.
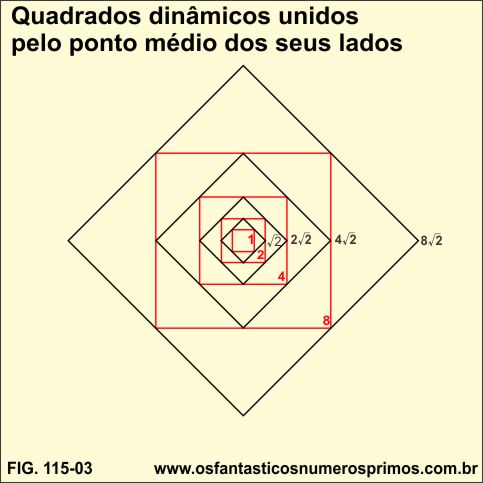
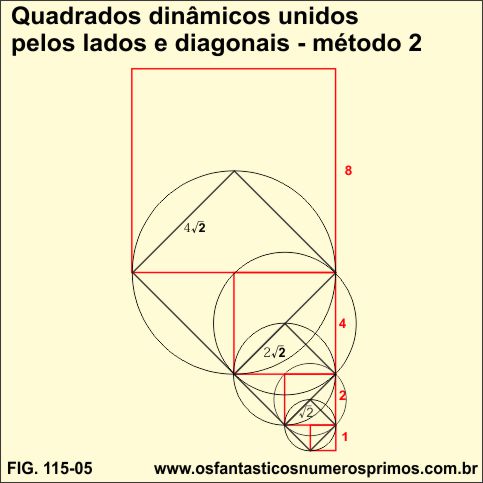
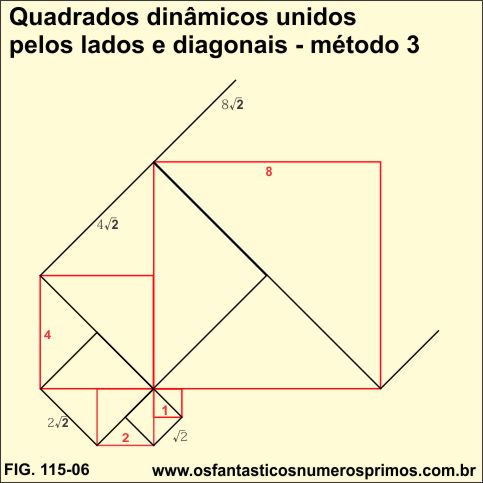
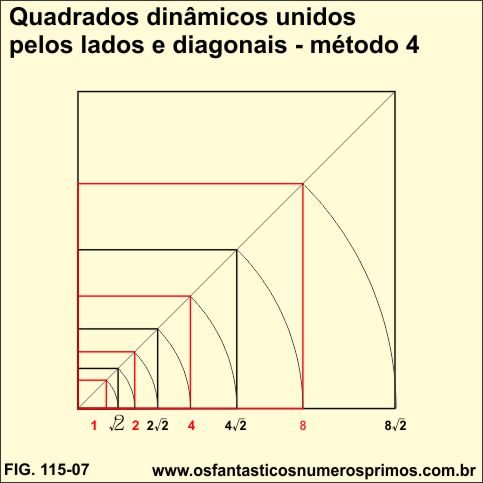
Além do passatempo, o que desperta a atenção é a construção geométrica dos quadrados unidos pelo ponto médio de seus lados.
A partir de um quadrado de lado 1 em contornos vermelho, desenha-se outros quadrados maiores, ligando-os através de seu ponto médio de seus lados. Enquanto os quadrados vermelhos, cujos os lados têm medidas de números inteiros: 1, 2, 4, 8, 16, 32, ... e vão dobrando de tamanho, formando uma progressão geométrica com as próprias medidas de seus lados: 1, 2, 4, 8, 16, 32, 64, 128, ..., os quadrados de contornos na cor preto subsequentes aos vermelhos têm as medidas dos seus lados a diagonal do quadrado vermelho anterior a ele, que é um número irracional e que também vão dobrando de tamanho:, 2√, 4√, 8√ ,..., e assim sucessivamente.
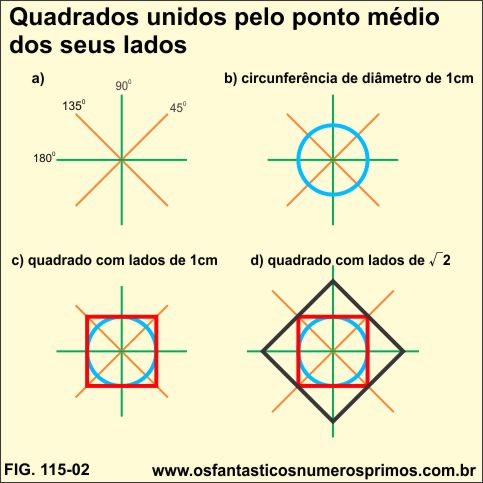
Seguindo os exemplos da figura 1:
a) faça seguimentos perpendiculares com as seguintes graduações: 45, 90, 135 e 180 graus;
b) faça uma circunferência de diâmetro de 1cm;
c) desenhe um quadrado vermelho sobre a circunferência;
d) desenhe um quadrado preto, cujos lados é a diagonal do quadrado de lado 1, seus vértices ficam sobre as linhas perpendiculares verde e o ponto médio de seus lados ficam sobre as linhas perperdiculares laranja e os vértices do quadrado vermelho.
Desenhando e intercalando quadrados, obtemos uma construção dinâmica de quadrados cujos lados têm medidas proporcionais, quadrados de lados de números inteiros e quadrados de lados de números irracionais.
Autor: Ricardo Silva - abril/2016
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato