


Ternos Pitagóricos apresentam diversos padrões e propriedades numéricas, umas das principais propriedades é que eles estão estritamente relacionados com o Teorema de Pitágoras.
Terno Pitagórico, também denominado de Tripla Pitagórica, Trinca Pitagórica é uma sequência de três números inteiros com os quais são possíveis de se construirem triângulos retângulos e que também os seus respectivos quadrados são números inteiros, isto é, não são números decimais e nem números irracionais.
Nos estudos publicados no livro digital Ternos Pitagóricos e Sequências Numéricas é demonstrado que Ternos Pitagóricos Primitivos se relacionam com a sequência de números triangulares, isto é, cada Terno Pitagórico Primitivo tem a sua ordem / posição um número triangular, sendo classificados das seguintes formas:
Ternos Pitagóricos Primitivos de ordem triangular
Ternos Pitagóricos Primitivos de ordem não triangular
Ternos Pitagóricos Derivados - triangular
Ternos Pitagóricos Derivados - não triangular
Ternos Pitagóricos Primitivos Raros
A tabela abaixo apresenta os 15 primeros Ternos Pitagóricos gerados por meio das Fórmulas de Euclides:
a = m² - n²
b = 2mn
c = m² + n²
onde:
m > n (m tem que ser maior que n)
m e n tem que ser primos entre si
Observação importante:
As Fórmulas de Euclides não geram ternos pitagóricos derivados ímpares.
As Fórmulas de Euclides geram ternos pitagóricos derivados da seguinte forma: o dobro, do dobro, do dobro, do dobro e assim sucessivamente de um terno pitagórico primitivo.
Exemplos de Ternos Pitagóricos derivados do terno 3-4-5:
6 - 8 - 10;
12 - 16 - 20;
24 - 32 - 40...
Observando cada sequência numérica em cada linha, num primeiro momento, umas parecem organizadas, outras desorganizadas, umas têm certa lógica de construção, outras não, mas estas observações são apenas aparentes, pois, os ternos pitagóricos se relacionam com várias outras sequências numéricas.
| 3 | 4 | 5 |
| 8 | 6 | 10 |
| 5 | 12 | 13 |
| 15 | 8 | 17 |
| 12 | 16 | 20 |
| 7 | 24 | 25 |
| 24 | 10 | 26 |
| 21 | 20 | 29 |
| 16 | 30 | 34 |
| 9 | 40 | 41 |
| 35 | 12 | 37 |
| 32 | 24 | 40 |
| 27 | 36 | 45 |
| 20 | 48 | 52 |
| 11 | 60 | 61 |
Númerando as sequências de Ternos Pitagóricos na ordem com que elas são geradas e destacando-as conforme características comuns: impar, par, ímpar e cujo primeiro termo é um número ímpar e o segundo e terceiro termos somados é um quadrado perfeito, percebe-se que suas ordens / posicões correspondem a números triangulares.
1, 3, 6, 10, 15,... são exemplos de números triangulares.
O intervalo entre um Terno Pitagórico Primitivo e outro, ocorre a sequência de números naturais:
a) entre os ternos 3-4-5 e 5-12-13 há 1 intervalo;
b) entre os ternos 5-12-13 e 7-24-25 há 2 intervalos e assim sucessivamente.
| Posições de Ternos Pitagóricos | |||
|---|---|---|---|
| ordem / | |||
| posição | Ternos Pitagóricos | ||
| 1 | 3 | 4 | 5 |
| 2 | 8 | 6 | 10 |
| 3 | 5 | 12 | 13 |
| 4 | 15 | 8 | 17 |
| 5 | 12 | 16 | 20 |
| 6 | 7 | 24 | 25 |
| 7 | 24 | 10 | 26 |
| 8 | 21 | 20 | 29 |
| 9 | 16 | 30 | 34 |
| 10 | 9 | 40 | 41 |
| 11 | 35 | 12 | 37 |
| 12 | 32 | 24 | 40 |
| 13 | 27 | 36 | 45 |
| 14 | 20 | 48 | 52 |
| 15 | 11 | 60 | 61 |
| www.osfantasticosnumerosprimos.com.br | |||
A soma de cada Terno Pitagórico Primitivo tem como resultado um número oblongo.
Números oblongos, também denominados de números retângulares, são números que são produtos de dois números consecutivos.
Números oblongos são números que são o dobro de um número triangular.
Dividindo-se um número oblongo (número retângular) por 2, obtem-se um número triangular.
12 : 2 = 6
30 : 2 = 15
56 : 2 = 28
90 : 2 = 45
132 : 2 = 66
6, 15, 28, 45, 66,... são números triangulares.
| Ternos Pitagóricos | ||||
|---|---|---|---|---|
| e números oblongos | ||||
| números | ||||
| oblongos | ||||
| posição/ | ||||
| ordem | Ternos Pitagóricos | soma | ||
| 1 | 3 | 4 | 5 | 12 |
| 2 | 8 | 6 | 10 | |
| 3 | 5 | 12 | 13 | 30 |
| 4 | 15 | 8 | 17 | |
| 5 | 12 | 16 | 20 | |
| 6 | 7 | 24 | 25 | 56 |
| 7 | 24 | 10 | 26 | |
| 8 | 21 | 20 | 29 | |
| 9 | 16 | 30 | 34 | |
| 10 | 9 | 40 | 41 | 90 |
| 11 | 35 | 12 | 37 | |
| 12 | 32 | 24 | 40 | |
| 13 | 27 | 36 | 45 | |
| 14 | 20 | 48 | 52 | |
| 15 | 11 | 60 | 61 | 132 |
| www.osfantasticosnumerosprimos.com.br | ||||
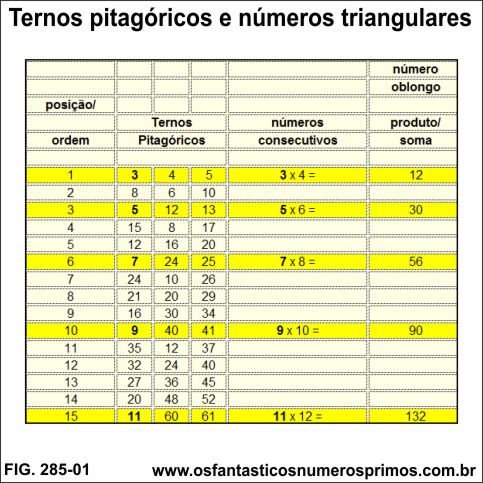
O produto do primeiro termo de um Terno Pitagórico Primitivo com o seu consecutivo tem como resultado o número oblongo que também é a soma dos termos desse mesmo terno pitagórico.
| Somas de Sequências de Ternos Pitagóricos | |||||
|---|---|---|---|---|---|
| número | |||||
| oblongo | |||||
| posição/ | |||||
| Ternos | números | produto/ | |||
| ordem | Pitagóricos | consecutivos | soma | ||
| 1 | 3 | 4 | 5 | 3 x 4 = | 12 |
| 2 | 8 | 6 | 10 | ||
| 3 | 5 | 12 | 13 | 5 x 6 = | 30 |
| 4 | 15 | 8 | 17 | ||
| 5 | 12 | 16 | 20 | ||
| 6 | 7 | 24 | 25 | 7 x 8 = | 56 |
| 7 | 24 | 10 | 26 | ||
| 8 | 21 | 20 | 29 | ||
| 9 | 16 | 30 | 34 | ||
| 10 | 9 | 40 | 41 | 9 x 10 = | 90 |
| 11 | 35 | 12 | 37 | ||
| 12 | 32 | 24 | 40 | ||
| 13 | 27 | 36 | 45 | ||
| 14 | 20 | 48 | 52 | ||
| 15 | 11 | 60 | 61 | 11 x 12 = | 132 |
| www.osfantasticosnumerosprimos.com.br | |||||
Autor: Ricardo Silva - setembro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato