capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Triângulo Pitagórico e semicircunferência - 294

Triângulo Pitagórico é um triângulo retângulo cujos lados são formados por um conjunto de três números inteiros, denominados de ternos pitagóricos que obedecem ao Teorema de Pitágoras: a²=b²+c² o qual apresenta o seguinte enunciado: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.

"Os babilônios já conheciam os ternos pitagóricos.

Os escribas babilônicos encheram suas tabuinhas com tabelas impressionantes de sequências de ternos exibindo a relação de pitágoras.

Eles registraram... outros ternos como 3.456, 3.367, 4.825. As chances de obter um terno que funcione, verificando três números ao acaso, são pequenas... A menos que os babilônios tenham empregado um exército de calculadores, que passaram toda a sua carreira fazendo cálculos, podemos concluir que eles conheciam, pelos menos, o suficiente da teoria dos números para gerar esses ternos."

Adaptado de A Janela de Euclides. Leonard Miodnow

Fonte: Coleção Tudo é Matemática, 9 ano, página 186, do Professor Luiz Robeto Dante, editado pela Editora Ática, edição 2011.

Na introdução da edição digital do livro, ano de 1968, The Pythagorean Propositions do Professor estadunidense Elisha Scott Loomis, páginas 17 a 21, o Professor apresenta 5 diferentes algoritmos para se gerarem ternos pitagóricos, inclusive uma de Euclides de Alexandria diferente da demonstrada a seguir.

Euclides de Alexandria, em seu livro Os Elementos, demonstrou que existe uma infinidade de ternos pitagóricos primitivos, além disso, encontrou fórmulas que geram todos os ternos pitagóricos primitivos.

Dados dois números naturais m > n, o terno (a,b,c), onde:

a = m² - n²

b = 2mn

c = m² + n²

é pitagórico, e é primitivo se e somente se m e n são primos entre si e possuem paridades distintas.

Observação importante:

Conforme estudos publicados nos livros digitais Ternos Pitagóricos e Sequências e Quadrados Mágicos e Sequências Numéricas, as Fórmulas de Euclides não geram ternos pitagóricos derivados ímpares.

As Fórmulas de Euclides geram ternos pitagóricos derivados da seguinte forma: o dobro, do dobro, do dobro, do dobro e assim sucessivamente de um terno pitagórico primitivo.

Exemplos de Ternos Pitagóricos Derivados do terno 3 - 4 - 5:

6 - 8 - 10;

12 - 16 - 20;

24 - 32 - 40...

Triângulo Pitagórico 3-4-5 e semicircunferência.

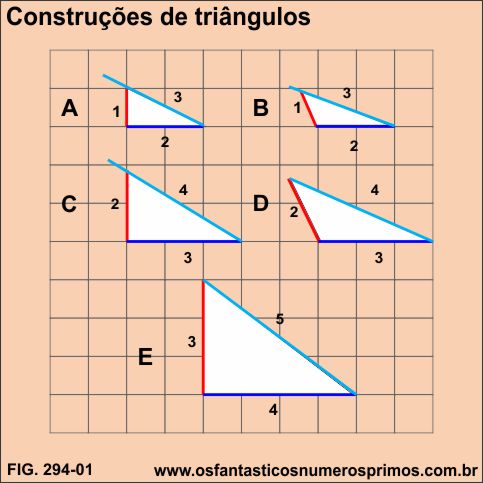
Escolhendo-se sequências de três números inteiros consecutivos e com elas formando seguimentos de reta e tentarmos construir triângulos, veremos que em alguns casos não são possíveis tais construções.

Nos exemplos A, B e C não foram possíveis de se construirem triângulos, mas nos exemplos D e E sim.

No exemplo D tem-se o primeiro exemplo de um triângulo obtusângulo cujos lados são formados por 3 números consecutivos.

No exemplo E tem-se o primeiro exemplo de um triângulo retângulo cujos lados são formados por 3 números consecutivos e que também é triângulo pitagórico.

Diâmetro dividido em partes iguais

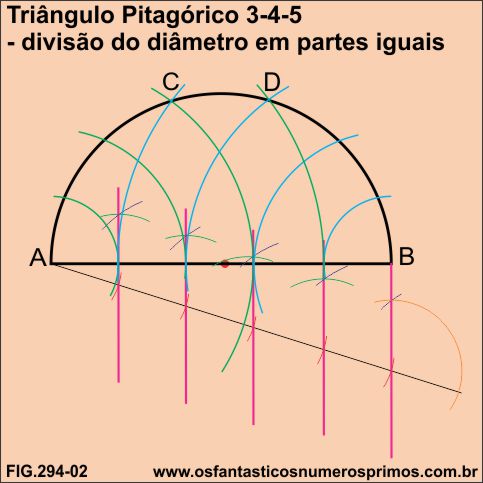
Todo triângulo inscrito numa semicircunferência é um triângulo retângulo, pois, dois dos seus vértices são os extremos do diâmetro e o terceiro vértice incide sobre a semicircunferência.

Numa semicircunferência cujo diâmetro for dividido em partes iguais e essas partes transportadas para a semicircunferência a partir dos extremos do diâmetro coincidirem em duplas, então os triângulos a serem formados são triângulos retângulos pitagóricos congruentes.

Aplicando a divisão de um segmento em 5 partes iguais em um diâmetro arbitrário de uma semicircunferência, foi possível determinar os pontos que incidem sobre a hipotenusa do triângulo retângulo 3-4-5 a ser inscrito.

Com a ponta seca em A, transporta-se os pontos do diâmetro para a semicircunferência por meio de arcos (cor verde).

Com a ponta seca em B, transporta-se os pontos do diâmetro para a semicircunferência por meio de arcos (cor azul).

Interessante observar que duas duplas de arcos se intersectam na semicircunferência: pontos C e D.

Os pontos C e D são os pontos que formarão os ângulos retos dos triângulos retângulos pitagóricos congruentes.

triângulo pitagórico 3-4-5 e divisão de diâmetro em partes iguais

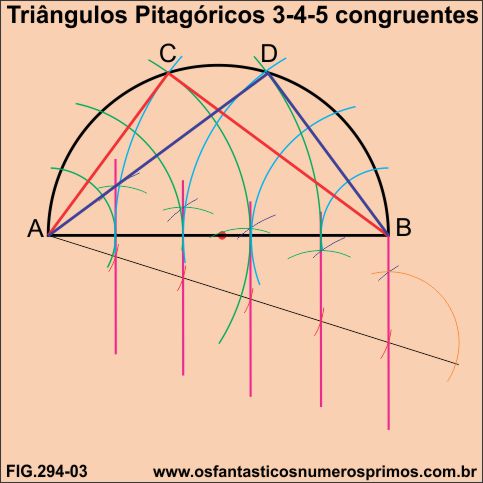
Unindo-se os pontos A, B e C forma-se o primeiro triângulo pitagórico 3-4-5.

Unindo-se os pontos A, B e D forma-se o segundo triângulo pitagórico 3-4-5.

triângulos pitagóricos 3-4-5 congruentes

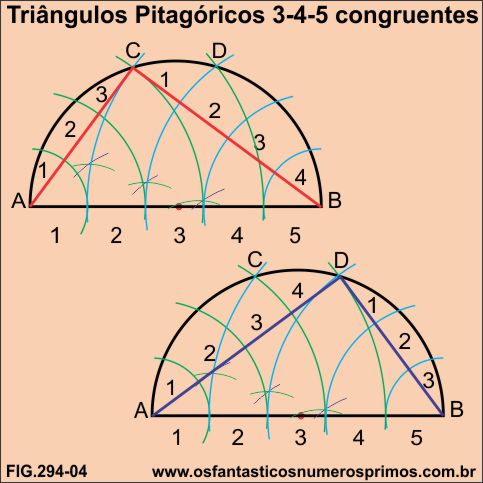
Numerando as divisões das partes das hipotenusas e dos catetos nos triângulos retângulos inscritos nas semicircunferências prova-se que são triângulos retângulos pitagóricos de lados 3-4-5 e congruentes.