


O homem, ao longo do tempo, para registrar suas ideias, pensamentos, emoções, etc..., fez o uso dos mais variados suportes como paredes de cavernas, rochas, tabletes de barro, papiros, pergaminhos, entre outros, realizando grafismos, desenhos, pinturas, símbolos e posteriormente alfabetos e números.
Um suporte que utilizamos bastante é o papel e que a partir dele, podem ser confeccionados folhas e blocos para desenhos, cadernos, formulários, livros, revistas, jornais, etc...
Em se tratando de folhas ou blocos de papel para desenhos, a sua forma é retangular e possui diversos formatos padrões, isto é, várias medidas quanto à suas larguras e comprimentos.
Folha de papel também pode representar um plano geométrico quando desenhamos figuras geométricas.
Seja numa folha em formato retangular ou numa folha em formato quadrado, determinando-se os pontos médios de seus lados e posteriormente traçando-se retas perpendiculares; ou ainda, traçando linhas diagonais, nos cruzamentos destas, pode-se desenhar circunferência centralizada no plano, bem como, traçar diâmetro jacente no plano.
Para mais informações, veja matérias relacionadas abaixo.
O questionamento que se faz é o seguinte: é possível a partir da própria circunferência, traçar um diâmetro jacente ao plano com régua e compasso ?
O presente estudo demonstra que traçando-se aleatoriamente uma reta passando pelo centro de uma circunferência e se esta reta tiver uma inclinação de ângulo notável: 30, 45 ou 60 graus, então é possível determinar um diâmetro jacente ao plano.
Dada uma circunferência de raio ou diâmetro qualquer, traça-se um reta que passa pelo seu centro.
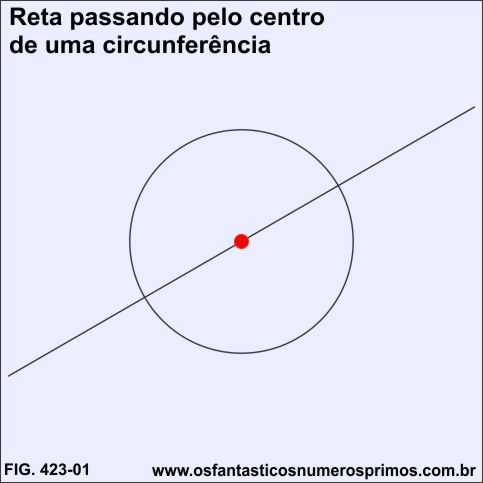
Duplica-se a circunferência de mesmo raio e cada uma com centro na primeira circunferência com a intersecção com a reta (pontos verde e azul).
Importante destacar que nesta construção geométrica tem-se a Vesica Piscis duplicada.

Traça-se uma reta concorrente pelos pontos de cores laranjas, formando-se ângulos opostos pelo vértice (ponto vermelho).
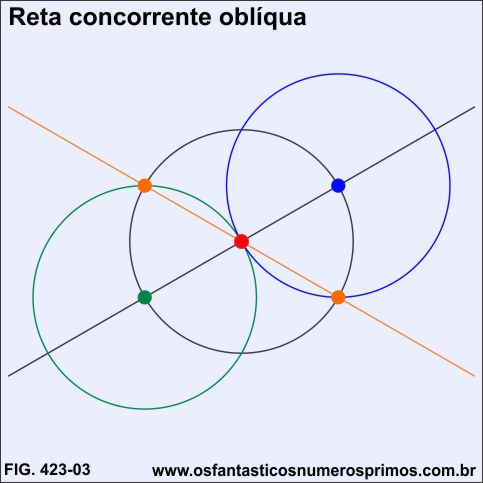
Traça-se uma outra circunferência (cor lilás) de mesmo raio que a primeira com centro (ponto laranja) e posteriomente a bissetriz (tracejada) do ângulo formado pelos pontos de cores azul, vermelho e laranja.
Prolonga-se a bissetriz (tracejada) para à esquerda.
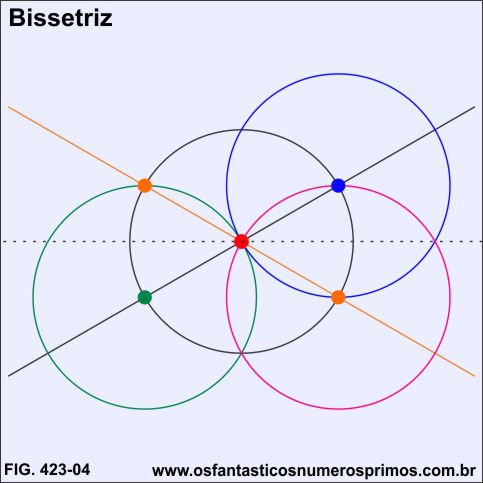
Traça-se uma reta perpendicular (cor marrom) pelos pontos vermelho e rosa até a alinha da base do quadrado (ponto azul).
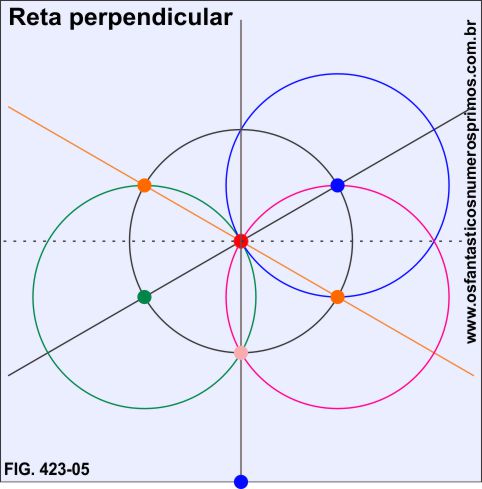
A partir da linha de base do quadrado, no ponto de cor azul, traça-se um arco, determinando os pontos de cores pretas.
Traçam-se arcos de mesma abertura em cada ponto preto da base do quadrado, na intersecção destes, marca-se o ponto de cor roxa.
A reta marrom é ao mesmo tempo perpendicular a reta tracejada e mediatriz dos pontos pretos da linha da base do quadrado, provando-se assim que a reta tracejada e a linha da base do quadrado são paralelas.
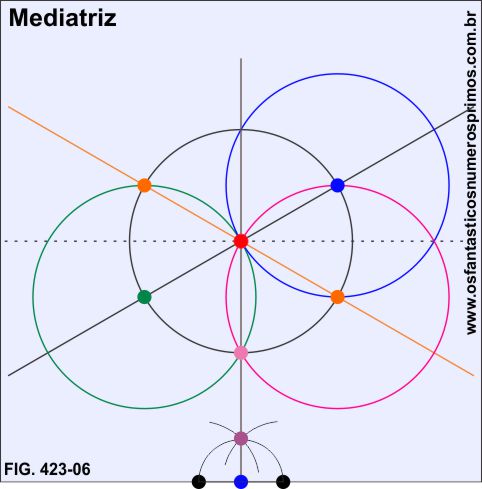
Reforçando parte da reta tracejada na circunferência (cor preta), tem-se então um diâmetro jacente ao plano a partir da própria circunferência
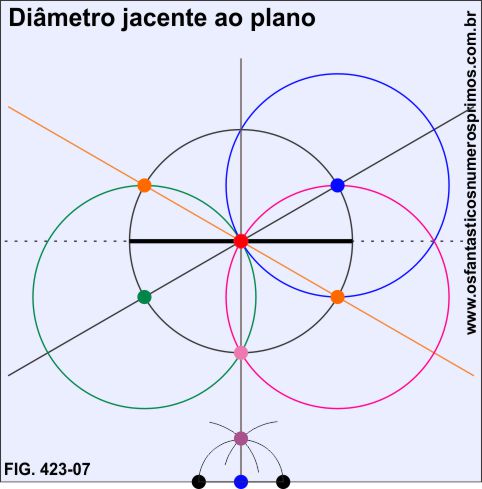
É possível traçar diâmetro pararelo ao plano a partir de retas secante e tangente numa circunferência.
Haverá alguma solução geométrica para este problema?
Autor: Ricardo Silva - janeiro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato