


Circunferência é a figura geométrica formada por infinitos pontos equidistantes de um ponto central e que pode ser desenhada utilizando-se compasso, objetos circulares como discos, tampas e até mesmo como fios, barbantes ou cordas cujas pontas tenham amarrados objetos que se possam riscar.
Por meio de circunferências podemos desenhar, isto é, inscrever e circunscrever diversos polígonos regulares, tais como, triângulos equiláteros, quadrados, pentágonos, hexágonos, etc.
O matemático grego, Arquimedes de Siracusa (287-212 a.C), em seus experimentos, para se tentar encontrar o valor "exato" do número Π (pi), inscreveu e circunscreveu numa circunferência um polígono de 96 lados. Em seus cálculos, efetuando-se as diferenças entre os perímetros dos polígonos inscrito e circunscrito chegou a aproximadamente entre 3,1408 e 3,1429 para o número Π (pi).[1]
360 graus : 96 lados = 3,75 graus (cada divisão)
Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou Π (pi) tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416.[1]
360 graus : 720 lados = 0,5 grau (cada divisão)
A "busca" pelo valor de Π (pi) chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados.[1]
360: 3.072 = 0,1171875 grau (cada divisão)
O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de Π (pi) com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de Π (pi) com as supracitadas 35 casas decimais.[1]
Duplicando-se o número 15 consecutivamente 37 vezes, na Planilha Microsoft Excel, não foi possível obter o valor legível da quantitade de lados que o matemático holandês Ludolph van Ceulen dividiu uma circunferência.
| Divisão da circunferência | |||||
|---|---|---|---|---|---|
| por Ludolph van Ceulen | |||||
| Quant. | divisão | divisão | |||
| vezes | da | da | |||
| circunferência | circunferência | ||||
| 1 | 15 | x | 2 | = | 30 |
| 2 | 30 | x | 2 | = | 60 |
| 3 | 60 | x | 2 | = | 120 |
| 4 | 120 | x | 2 | = | 240 |
| 5 | 240 | x | 2 | = | 480 |
| 6 | 480 | x | 2 | = | 960 |
| 7 | 960 | x | 2 | = | 1920 |
| 8 | 1920 | x | 2 | = | 3840 |
| 9 | 3840 | x | 2 | = | 7680 |
| 10 | 7680 | x | 2 | = | 15360 |
| 11 | 15360 | x | 2 | = | 30720 |
| 12 | 30720 | x | 2 | = | 61440 |
| 13 | 61440 | x | 2 | = | 122880 |
| 14 | 122880 | x | 2 | = | 245760 |
| 15 | 245760 | x | 2 | = | 491520 |
| 16 | 491520 | x | 2 | = | 983040 |
| 17 | 983040 | x | 2 | = | 1966080 |
| 18 | 1966080 | x | 2 | = | 3932160 |
| 19 | 3932160 | x | 2 | = | 7864320 |
| 20 | 7864320 | x | 2 | = | 15728640 |
| 21 | 15728640 | x | 2 | = | 31457280 |
| 22 | 31457280 | x | 2 | = | 62914560 |
| 23 | 62914560 | x | 2 | = | 125829120 |
| 24 | 125829120 | x | 2 | = | 251658240 |
| 25 | 251658240 | x | 2 | = | 503316480 |
| 26 | 503316480 | x | 2 | = | 1006632960 |
| 27 | 1006632960 | x | 2 | = | 2013265920 |
| 28 | 2013265920 | x | 2 | = | 4026531840 |
| 29 | 4026531840 | x | 2 | = | 8053063680 |
| 30 | 8053063680 | x | 2 | = | 16106127360 |
| 31 | 16106127360 | x | 2 | = | 32212254720 |
| 32 | 32212254720 | x | 2 | = | 64424509440 |
| 33 | 64424509440 | x | 2 | = | 1,28849E+11 |
| 34 | 1,28849E+11 | x | 2 | = | 2,57698E+11 |
| 35 | 2,57698E+11 | x | 2 | = | 5,15396E+11 |
| 36 | 5,15396E+11 | x | 2 | = | 1,03079E+12 |
| 37 | 1,03079E+12 | x | 2 | = | 2,06158E+12 |
Efetuando-se o cálculos na Calculadora Científica do Microsof Windows, a circunferência ficou dividida em: 515.396.075.520 lados.
360 graus : 515.396.075.520 lados =
0,000000
Obtêm-se potências de base 2 elevando-se o número 2 a expoentes com números naturais ou através da multiplicação cujos fatores é o próprio número 2.
20 = 1
21 = 2
22 = 2 x 2 = 4
23 = 2 x 2 x 2 = 8
24 = 2 x 2 x 2 x 2 = 16
25 = 2 x 2 x 2 x 2 x 2 = 32
As potências de base 2 apresentam um diferencial entre os demais números pares, pois, a partir da unidade, isto é, do número 1, dobrando-se os resultados, obtem-se potências de base 2:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,...
Dividindo-se potências de base 2 pela metade, chega-se a unidade:
1024 : 2 = 512
512 : 2 = 256
256 : 2 = 128
128 : 2 = 64
64 : 2 = 32
32 : 2 = 16
16 : 2 = 8
8 : 2 = 4
4 : 2 = 2
2 : 2 = 1
O mesmo não acontece com determinados números pares como: 6, 10, 12, 14, 18 e outros.
6 : 2 = 3
3 : 2 = 1,5
10 : 2 = 5
5 : 2 = 2,5
14 : 2 = 7
7 : 2 = 3,5
Geometricamente para se dividir uma circunferência em partes iguais, podemos utilizar o método da bissetriz, que consiste em dividir um ângulo em duas partes congruentes.
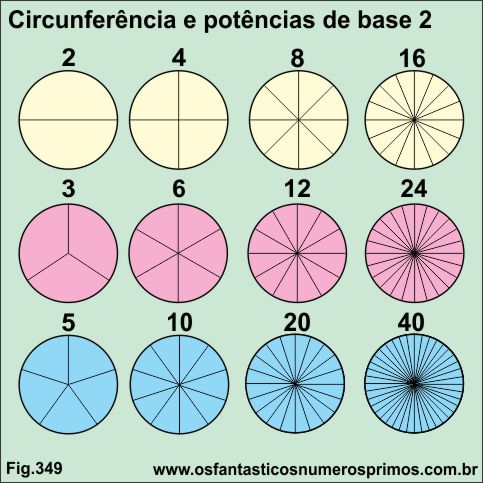
Dividindo a circunferência, que corresponde a 360 graus sempre pela metade, obtem-se partes cuja sequência são formadas por potências de base 2: 2, 4, 8, 16, 32, 64, 128,...
As divisões sucessivas de uma circunferência por potências de base 2 têm como resultados partes cujos números são inteiros ao passo que a divisões em graus a partir de 16 partes, os números em graus são decimais.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por partes (potências) | |||||
| de base 2 | |||||
| Partes | |||||
| 360 | : | 2 | = | 180 | graus |
| 360 | : | 4 | = | 90 | graus |
| 360 | : | 8 | = | 45 | graus |
| 360 | : | 16 | = | 22,5 | graus |
| www.osfantasticosnumerosprimos.com.br | |||||
Dividindo a circunferência, começando por 3 partes e dobrando-se os resultados, obtem-se a progressão geométrica: 3, 6, 12, 24, 48, ... de razão 2:
As divisões sucessivas de uma circunferência por múltiplos de 3, de razão 2, têm como resultados partes cujos números são inteiros ao passo que a divisões em graus a partir de 48 partes, os números em graus são decimais.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 3 | |||||
| Partes | |||||
| 360 | : | 3 | = | 120 | graus |
| 360 | : | 6 | = | 60 | graus |
| 360 | : | 12 | = | 30 | graus |
| 360 | : | 24 | = | 15 | graus |
| 360 | : | 48 | = | 7,5 | graus |
| www.osfantasticosnumerosprimos.com.br | |||||
A multiplicação do número 3 por potências de base 2 têm como produtos quantidades de divisões da circunferência por múltiplos de 3 de razão 2.
3 x 1 = 3
3 x 2 = 6
3 x 4 = 12
e assim sucessivamente.
Dividindo a circunferência, começando por 5 partes e dobrando-se os resultados, obtem-se a progressão geométrica: 5, 10, 20, 40, 80, ... de razão 2:
As divisões sucessivas de uma circunferência por múltiplos de 5, de razão 2, têm como resultados partes cujos números são inteiros ao passo que a divisões em graus a partir de 80 partes, os números em graus são decimais.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 5 | |||||
| Partes | |||||
| 360 | : | 5 | = | 72 | graus |
| 360 | : | 10 | = | 36 | graus |
| 360 | : | 20 | = | 18 | graus |
| 360 | : | 40 | = | 9 | graus |
| 360 | : | 80 | = | 4,5 | graus |
| www.osfantasticosnumerosprimos.com.br | |||||
A multiplicação do número 5 por potências de base 2 têm como produtos quantidades de divisões da circunferência por múltiplos de 5 de razão 2.
5 x 1 = 5
5 x 2 = 10
5 x 4 = 20
e assim sucessivamente.
Dividindo a circunferência, começando por 9 partes e dobrando-se os resultados, obtem-se a progressão geométrica: 9, 18, 36, 72, 144, ... de razão 2:
As divisões sucessivas de uma circunferência por múltiplos de 9, de razão 2, têm como resultados partes cujos números são inteiros ao passo que a divisões em graus a partir de 144 partes, os números em graus são decimais.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 9 | |||||
| Partes | |||||
| 360 | : | 9 | = | 40 | graus |
| 360 | : | 18 | = | 20 | graus |
| 360 | : | 36 | = | 10 | graus |
| 360 | : | 72 | = | 5 | graus |
| 360 | : | 144 | = | 2,5 | graus |
| www.osfantasticosnumerosprimos.com.br | |||||
A multiplicação do número 9 por potências de base 2 têm como produtos quantidades de divisões da circunferência por múltiplos de 9 de razão 2.
9 x 1 = 9
9 x 2 = 18
9 x 4 = 36
e assim sucessivamente.
Dividindo a circunferência, começando por 15 partes e dobrando-se os resultados, obtem-se a progressão geométrica: 15, 30, 60, 120, 240, ... de razão 2:
As divisões sucessivas de uma circunferência por múltiplos de 15, de razão 2, têm como resultados partes cujos números são inteiros ao passo que a divisões em graus a partir de 240 partes, os números em graus são decimais.
| Divisão de circunferência | |||||
|---|---|---|---|---|---|
| por múltiplos de 15 | |||||
| Partes | |||||
| 360 | : | 15 | = | 24 | graus |
| 360 | : | 30 | = | 12 | graus |
| 360 | : | 60 | = | 6 | graus |
| 360 | : | 120 | = | 3 | graus |
| 360 | : | 240 | = | 1,5 | graus |
| www.osfantasticosnumerosprimos.com.br | |||||
A multiplicação do número 15 por potências de base 2 têm como produtos quantidades de divisões da circunferência por múltiplos de 15 de razão 2.
15 x 1 = 15
15 x 2 = 30
15 x 4 = 60
e assim sucessivamente.
Autor: Ricardo Silva - outubro/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[1] "https://pt.wikipedia.org/w

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato