


Utilizando régua e compasso e como suporte, por exemplo, folha de papel formato A4, podemos fazer uso de retas concorrentes perpendiculares ou oblíquas e no cruzamentos destas colocar a ponta seca do compasso e desenhar circunferência de raio ou diâmetro qualquer.
Fazendo-se o uso de retas concorrentes perpendiculares ou oblíquas, pode-se desenhar circunferência centralizada na folha de papel e traçando-se em um dos ângulos horizontal a bissetriz e assim determinar o diâmetro horizontal e este alinhado e paralelo ao plano.
Para mais informações, veja matérias relacionadas abaixo.
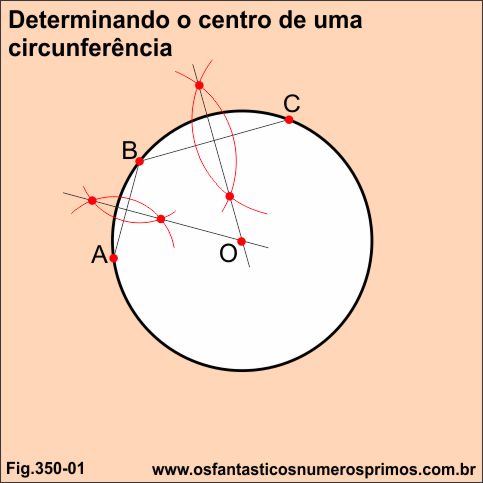
Seja uma circunferência de raio ou diâmetro qualquer.
Marcam-se 3 pontos aleatórios sobre a circunferência e posteriormente traçamos as mediatrizes dos seguimentos AB e BC.
Na intersecção das duas mediatrizes, o ponto O, é centro da circunferência.
Neste tipo de construção geomética, fica a seguinte pergunta: como determinar o diâmetro horizontal de uma circunferência ou ainda, como alinhar a circunferência no plano a partir da própria circunferência?
Pesquisas realizadas em geometria plana nos tópicos de relações métricas no triângulo retângulo e circunferência em livros do ensino médio, teses de mestrados, ensaios, apostilas, vídeo-aulas e websites constatou-se que não há exemplos ou demonstrações geométricas de como determinar o diâmetro horizontal de uma circunferência com régua e compasso a partir da própria circunferência.
As construções geométricas a seguir tem como referência a construção de retas paralelas do livro Realidade Matemática - 80 ano - página 95 - as quais foram utilizadas para se determinar o diâmetro horizontal de uma circunferência com régua e compasso a partir de transporte de ângulo.
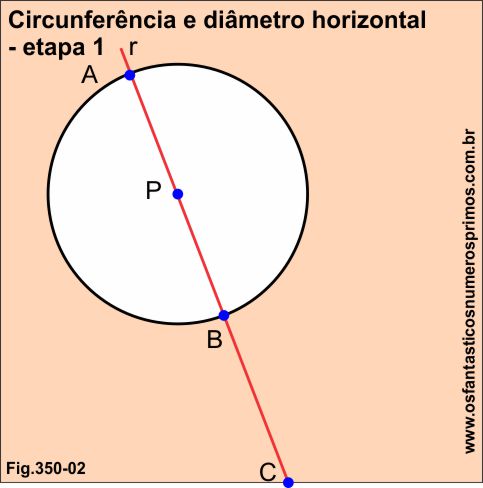
etapa 1
Seja um ponto P aleatório num plano, desenha uma circunferência de raio ou diâmentro qualquer, traça-se uma reta secante e ao mesmo tempo concorrente r até a base do plano, determinando-se assim os pontos A, B, C;
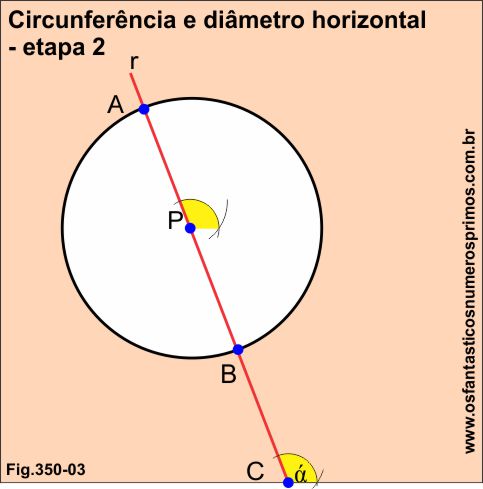
etapa 2
Na intersecção do ponto C com a base do plano, traça um ângulo α (alpha) e o transporta para o ponto P;
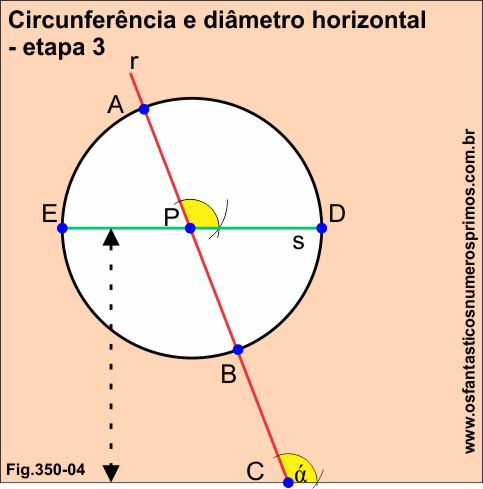
etapa 3
Traça-se um seguimento a partir de P, passando pelo ângulo α (alpha) até a circunferência, determinando o ponto D, prolongando o seguimento para esquerda, determinando o ponto E.
O seguimento ED é o diâmetro horizontal da circunferência e este se encontra paralelo ao plano.
Neste exemplo de demonstração geométrica, o diâmetro paralelo ao plano foi obtido em função da linha de contorno inferior do próprio plano, isto é, de um elemento auxiliar e externo à circunferência.
Autor: Ricardo Silva - outubro/2021
EUCLIDES. Os elementos/Euclides; tradução e introdução de Irineu Bicudo. – São Paulo: Editora UNESP, 2009. 600p.: il.
IEZZI, Gelson. Matêmática e realidade: 80 ano / Gelson Iezzi, Osvaldo Dolce, Antonio Machado. - 6. ed. - São Paulo: Atual, 2009
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato