


Todo triângulo inscrito numa semicircunferência é um triângulo retângulo.
Triângulo retângulo de ângulos de 30, 60 e 90 graus pode ser inscrito numa semicircunferência com régua sem gradução e compasso, pois é possível com o compasso determinar sob a semicircunferência o vértice em que será construído o ângulo de 90 graus a partir de um dos extremos do diâmetro ao seu ponto médio traçando um arco intersectando a semicircunferência e assim unir os extremos do diâmentro formando o triângulo retângulo.
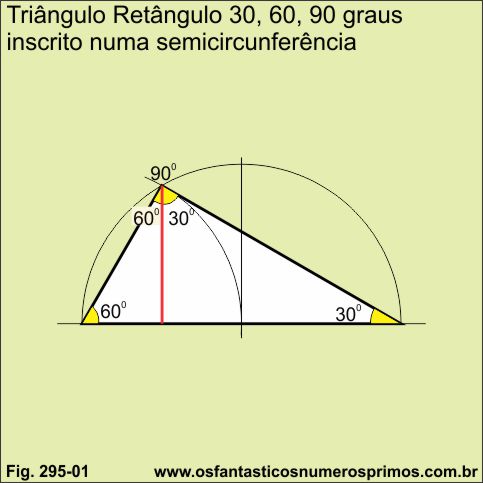
Triângulo retângulo de ângulos de 30, 60 e 90 graus e equiláteros podem ser inscritos na Vesica Piscis.
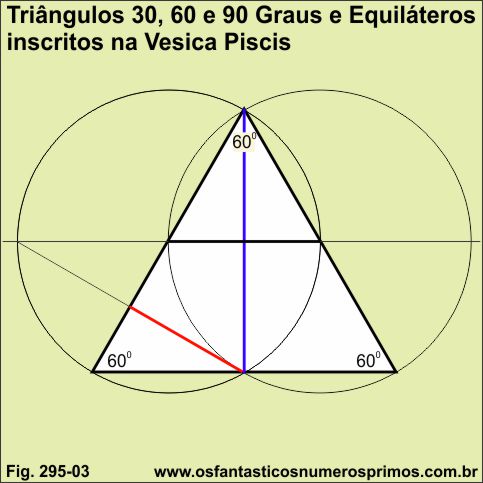
Triângulo ísóceles pode ser inscrito numa semicircunferência com régua sem graduação e compasso traçando-se uma reta perpendicular do ponto médio do diâmetro até a semicircunfência, ponto este que será o vértice que formará o ângulo de 90 graus, unindo-o aos extremos do diâmetro tem-se um triângulo retângulo isóceles.
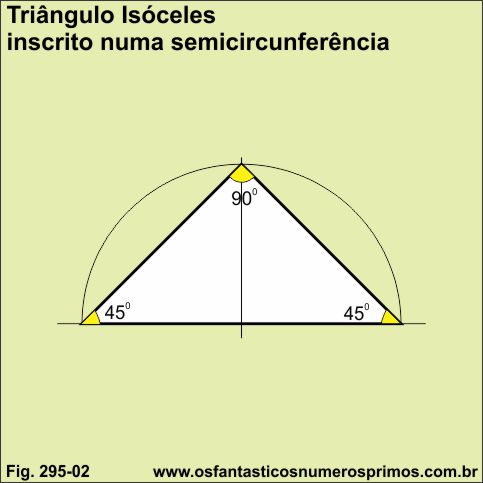
Triângulo Pitagórico é um triângulo retângulo cujas medidas dos lados são formados por um conjunto de três números inteiros, denominados de ternos pitagóricos, que tem relação com o Teorema de Pitágoras a²=b²+c² o qual apresenta a seguinte proposição: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
Para inscrever um triângulo pitagórico numa semicircunferência necessariamente precisamos dividir o diâmetro em partes iguais e a partir dessas partes tomar a medida do cateto menor e a medida do cateto maior ou fazer uso de régua graduada para construir o triângulo pitagórico.
Triângulos Pitagóricos não possuem ângulos agudos notáveis de 30 e 60 graus, mas as medidas dos seus lados são formadas por números inteiros.
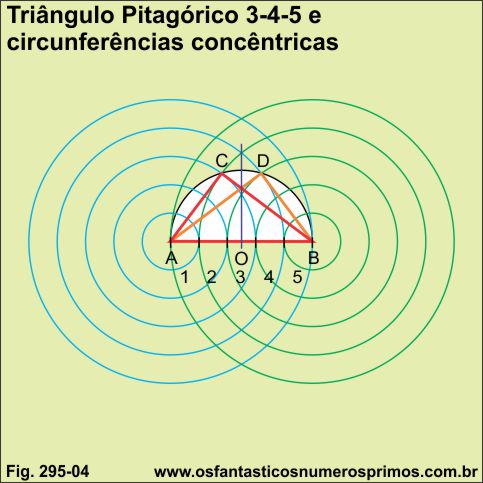
A partir de construções de dois conjuntos de n circunferências concêntricas de centros equidistantes são possíveis de se construirem triângulos retângulos pitagóricos.
a) contrói-se um seguimento de reta de extremidades A e B;
b) dividi-se os seguimento em partes iguais, no exemplo: 5 partes;
c) constroem-se 5 circunferências concêntricas a partir de cada extremidade A e B;
d) marca-se o ponto médio O na reta A e B;
e) a partir do ponto médio O, traça-se um semicircunferência de extreminades A e B;
f) dois pares de circunferências intersectam a semicircunferência nos pontos C e D;
g) os pontos C e D são vértices que formarão ângulos de 90 graus e consequentemente os catetos dos triângulos retângulos;
h) unindo-se os pontos A, B e C forma-se o primeiro triângulo retângulo pitagórico 3-4-5;
i) unindo-se os pontos A, B e D forma-se o segundo triângulo retângulo pitagórico 3-4-5.
Interessante observar que nestas construções geométricas, elas se assemelham a Vesica Piscis e a Mandorla.
A Vesica Piscis é a intersecção de duas circurferências cujo centro de cada uma se encontra no perímetro da outra.
A Mandorla é a região formada pela intersecção de dois arcos de circunferências, a palavra Mandorla significa amêndoa em italiano.
Outro ponto a destacar é que as intersecções das duplas de circunferências na semicircunferência criam também "pontos notáveis" a partir de partes do termo do terno pitagórico que se refere a medida da hipotenusa, determinado-se assim o vértice e as medidas dos catetos no triângulo retângulo.
O modelo matemático demonstrado anteriormente pode ser sintetizado, isto é, pode ser construído com arcos de circunferências e assim economizar tempo de execução.
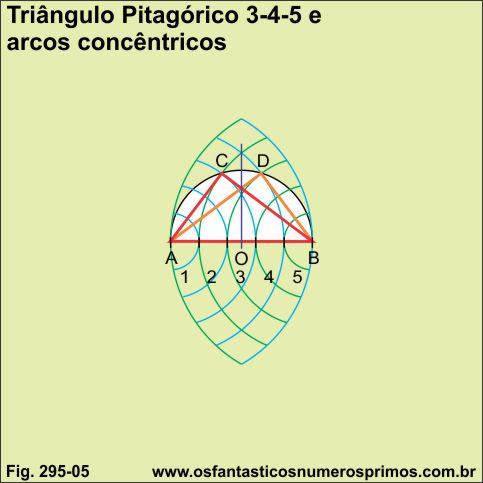
A partir de um segmento dividido em 5 partes iguais foi possível verificar e comprovar por meio de circunferências concêntricas e uma semicircunferência que os números 3-4-5 é um terno pitagórico e construir triângulo retângulo.
Podemos também verificar e comprovar se outros números inteiros fazem parte de um dos termos de um terno pitagórico.
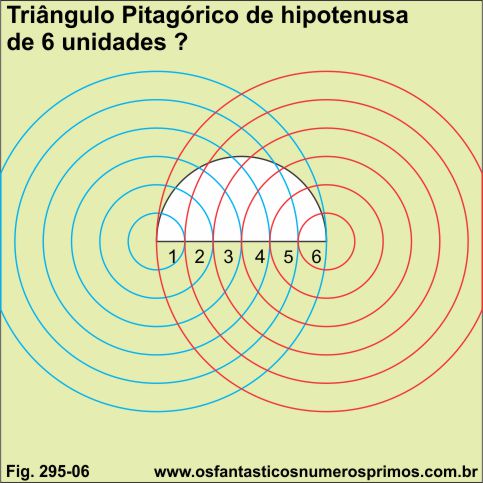
No exemplo, temos um segmento dividido em 6 partes iguais, com circunferências concêntricas e a semicircunferência.
Conforme podemos comprovar, não foi possível formar dois pares de circunferências que intersectam a semicircunferência, portanto o número 6 não a medida da hipotenusa em um triângulo pitagórico.
Autor: Ricardo Silva - outubro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato