


Em 10 de junho de 2008, na área rural Barbury Castle de Wiltshire na Inglaterra, apareceu um Agroglifo, também denominado de Crop Cicle ou ainda Círculos nas Plantações.
Agroglifos são enormes desenhos formados por diversas figuras geométricas como se tivessem sido carimbados sobre plantações de milho, canola, cevada e outras, dando a impressão de um desenho em alto relevo.
Agroglifos, Crop Cicles não são "fenômenos" modernos, em uma xilogravura inglesa do século XVII chamada de o "Demônio Ceifador" retrata o diabo com uma foice cortando com um desenho circular num campo de aveia conforme lendas e boatos da época.
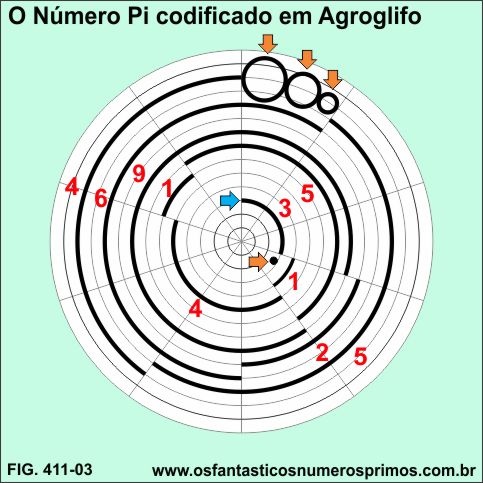
O Agroglifo de Barbury Castle apresenta em sua construção uma característica bastante peculiar que foi descoberta pelo Astrofísico Mike Reed que são os 10 primeiros algarismos do número número Π (pi) 3.141592654 codificado por arcos de circunferências.
Quem quer que o tenha produzido o Agroglifo de Barbury Castle, tinha bons conhecimentos de Geometria e técnicas de escultura, pois fazer as circunferências concêntricas em formas de sulcos numa plantação seja de milho, canola, cevada ou outras culturas sem danificar o relevo sendo formado que caracteriza a construção geométrica em si, é um trabalho de um gênio.
Tomando como referência a fotografia publicada no commons.wikimedia.org, foram realizadas várias etapas para se entender melhor a construção geométrica do Agroglifo de Barbury Castle.
Desenhou uma circunferência (cor azul) contornando o sulco central na imagem.
Traçou-se um seguimento de reta (cor amarelo) da circunferência azul até o próximo sulco, seguimento este que serviu para se saber a distância de um sulco a outro, em outras palavras, a distância entre uma circunferência e outra e também para se saber as quantidades de circunferências.
Encontrou-se 14 circunferências concêntricas.
Reparar que as circunfêrencias (sulcos) de números 1 e 13 não aparecem no Agroglifo e a circunferência final é a 14 que delimita o agroglifo.

Fonte: https:
O Agroglifo de Barbury Castle possui diâmetro de 150 pés que convertidos em metros são aproximadamente 45,72 metros.
45,72 metros divididos por 14 circunferências é igual a 3,2657..., um número um pouco maior que o Π (pi).
A circunferência é divida em 10 partes.
360 graus dividido por 10 tem como resultado 36 graus cada setor.
O decágono é um polígono regular que decomposto em triângulos, os ângulos internos agudos são 36, 72, 72, ângulos estes de um Triângulo Sublime, também denominado de Triângulo Áureo.
Observação importante: o diagrama abaixo foi produzido utilizando-se programa de computador de desenho vetorial e que possui ferramenta para se desenhar decágono.
Lembrando que os demais métodos abaixo relacionados, também se podem construir decágonos:
1) com régua e compasso utilizando-se parte da construção geométrica de um pentágono;
2) com régua e compasso utilizando o Método Rinaldini;
3) com o uso de transferidor;
4) a partir da Vesica Piscis.

A partir da 3a circunferência central em sentido horário (seta azul), os arcos construídos são os algarismos do número Π (pi) 3.141592654 codificado no Agroglifo de Barbury Castle.
Interessante observar que o primeiro algarismo do Pi, o 3, começa exatamente na terceira circunferência.
O ponto que aparece após o arco que representa o algarismo 3, é o ponto que divide a parte inteira da parte decimal do Π (pi) e as 3 circunferências que estão no topo, são as reticências representando a infinidade do Π (pi) (setas laranja) segundo alguns estudiosos de agroglifos.
Observação: ao fazermos um ponto ou reticências com lápis ou caneta, simplesmente presionamos uma vez, para um ponto e 3 vezes para reticências e de uma forma mecânica.
A questão é: porque as "reticências" estâo representadas por circunferências com as mesmas espessuras do arcos que representam os algarismos do número Π (pi) e em tamanhos diferentes.
Não haveria ai uma outra mensagem a ser decodificada?
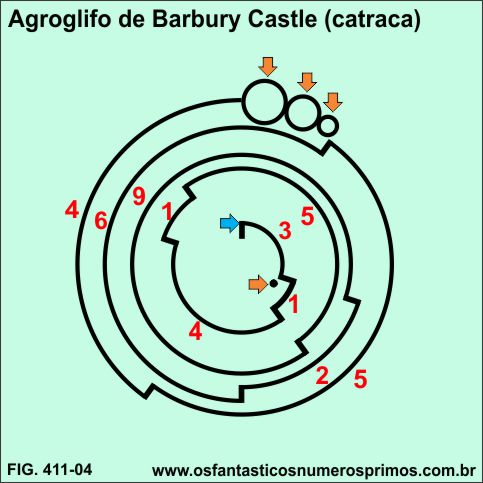
Deixando em destaque somente os seguimentos que formam os sulcos do Agroglifo de Barbury Castle, percebe-se que a figura se parece com algum tipo de catraca.
A intenção de se demonstrar a reconstrução deste agroglifo é mostrar que ele exigiu diversas etapas e aplicação de conhecimento básico de geometria e veja que está sendo demonstrado com desenhos realizados em um programa de desenho vetorial.
Imagine você, estimado visitante, realizar esta obra geométrica em alguma plantação de cereal, necessitaria de outras técnicas e bem avançadas para deixá-la igual ao da fotografia acima.
Outro detalhe que chamou bastante a minha atenção, bastante mesmo a minha atenção, é que as circunferências de números 11 e 12, bem como, as 3 circunferências (reticências) formam um grande muro, perfeitamente circular, protegendo as construções geométricas internas.
Vendo e revendo a fotografia, é como se alguém tivesse utilizado um enorme carimbo e feito as formas que ali aparecerem.
Em vez de pantação de milho, canola ou cevada, etc..., será que seria fácil realizar esta construção geométrica num campo de futebol com a grama bem alta?
Autor: Ricardo Silva - dezembro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https:
https:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato