logotipo os fantasticos numeros primos
capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo
Página de estudos de matemática e sequências numéricas

Restos de Divisões e Sequências Numéricas - 564

Em estudos divulgados aqui no WebSite Os Fantásticos Números Primos, bem como, publicados no livro digital Ternos Pitagóricos e Sequências Numéricas, descobriu-se que Ternos Pitagóricos Primitivos têm suas ordens / posições números triangulares e seus respectivos ternos derivados estão em progressão geométrica, isto é, os ternos derivados são o dobro, do dobro, do dobro, e assim, sucessivamente..., de um terno pitagórico primitivo, regularidades estas inéditas e que até o presente momento não constam em outras publicações, tais como, livros, teses de mestrados, artigos, ensaios, etc.

O presente estudo demonstra que restos de divisões entre potências de uma base natural (neste estudo, potências de base 2) e um número que não contem fator primo com essa base apresentam sequências numéricas formadas por progressões geométricas, progressões aritméticas, bem como, duplas de dobros de restos.

Cálculos em computador quântico

No vídeo cujo título: Como os Computadores Quânticos Quebram a Internet… A Partir de Agora [1] da Veritasium em Português, no tempo de 12 minutos e 38 segundos, discorre sobre como computadores quânticos efetuam cálculos para fatorar N, como produto de 2 números primos em relação ao processamento de um computador convencional por meio da seguinte fórmula:

g^r = m N + 1

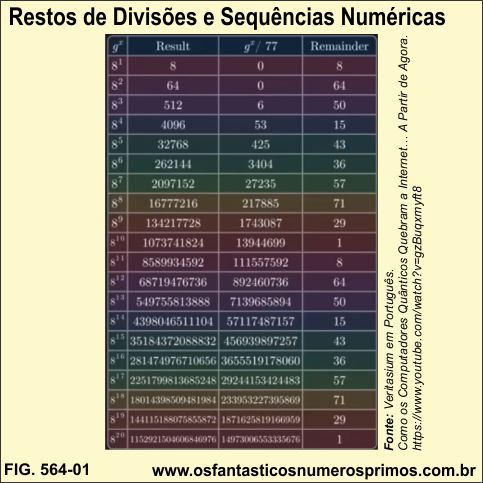
É demonstrado que um número (N), no exemplo 77, que não tem fator primo com um número (g), no exemplo 8, e que as potências desse número (g) em determinado momento sempre terá 1 unidade de diferença (resto) em relação a um múltiplo de (N).

No exemplo, 8 ^10...

base expoente potência divisor quociente múltiplo resto 
8         de  
          77  
             
8 10 1073741824 77 13944699 1073741823 1
(g^r/2 + 1) = m N
(g^r/2 - 1) = m N

Então eleva-se 8^10/2 mais 1 e 8^10/2 menos 1:

(8^10/2 + 1) = (8^5 + 1) = 32.769

(8^10/2 - 1) = (8^5 - 1) = 32.767

Os números 32.769 e 32.767 são fatores de 1.073.741 823.

32.769 x 32.767 = 1.073.741.823

1.073.741.823 é um múltiplo de 77

O número 1.073.741.823 é 1 unidade menor que 8^10 = 1073741824

base expoente potência divisor quociente múltiplo resto 
8         de  
          77  
             
8 1 8 77 0 0 8
8 2 64 77 0 0 64
8 3 512 77 6 462 50
8 4 4096 77 53 4081 15
8 5 32768 77 425 32725 43
8 6 262144 77 3404 262108 36
8 7 2097152 77 27235 2097095 57
8 8 16777216 77 217885 16777145 71
8 9 134217728 77 1743087 134217699 29
8 10 1073741824 77 13944699 1073741823 1
             

Fonte: adaptado de Veritasium em Português. Como os Computadores Quânticos Quebram a Internet… A Partir de Agora. https://www.youtube.com/watch?v=gzBuqxmyft8

Então os números 32.769 e 32.767 também possuem fatores primos comuns do número 77.

Para comprovar este fato, efetuam-se o mdc (máximo divisor comum) por meio do Algoritmo de Euclides.

mdc (32.769, 77) =11

mdc (32.767, 77) = 7

7 x 11 = 77

ou

77 / 11 = 7

Os fatores primos de N (77) são 7 e 11.

Esses cálculos, segundo a Veritasium, efefuados em computadores quânticos são "centenas e centenas" de vezes muito mais rápidos que computadores convencionais (ano 2025).

Interessante observar que o último Primo de Mersenne (ano 2024, 2^136.279.841 - (M136279841)) com 41.024.320 dígitos foi descoberto com uma GPU (Unidade de Processamento Gráfico) da NVIDIA, que segundo especialistas, a capacidade de processamento é maior do que processador da INTEL.

Numa segunda etapa é demonstrado que a rapidez de um computador quântico se dá porque há um padrão nos restos das divisões, isto é, os restos se repetem em intervalos regulares.

Veja que nas linhas onde 8^1, 8^11 e 8^21, o resto 8 é o mesmo, os restos se repetem de 10 em 10 intervalos, o mesmo para os demais restos.

Restos de Divisões e sequencias numéricas

Potências de base 2 e restos de divisões por 77

A tabela a seguir apresenta as 60 primeiras potências de base 2 e os restos das divisões por 77.

Diferentemente da tabela demonstrada no vídeo da Veritasium, a tabela a seguir apresenta outras propriedades numéricas em sua estrutura, vejamos:

a) realmente os restos se repetem em intervalos regulares conforme demonstrados no vídeo.

b) determinados restos formam grupos de progressões geométricas, outros, grupos de dobros de restos:

grupo de PG: 1, 2, 4, 8, 16, 32, 64;

grupo de PG: 15, 30, 60;

grupo de PG: 9, 18, 36, 72;

grupo de dobro: 25, 50;

grupo de dobro: 23, 56;

grupo de dobro: 37, 74;

grupo de dobro: 29, 58;

Interessante observar que as sequências começam com números ímpares e, entre eles, número primos.

c) interessante observar que os primeiros restos de 1 a 64 não têm "serventias práticas", pois tanto os quocientes quanto os múltiplos são todos 0 (zeros).

d) a soma de 30 restos cujas ordens / posições são:

de 0 a 29,

de 30 a 59,

de 60 a 99,

e assim sucessivamente... é 1155.

1155 é múltiplo de 7.

1155 / 77 = 15

15 é a metade da quantidade de restos.

Observação: esta propriedade não aparece na tabela cuja a base é 8, no exemplo da Veritasium, pois a soma dos restos é 374.

374 não é múltiplo de 77.

e) os quocientes também apresentam:

grupos de dobros

3 e 6

13 e 26

e outros

grupos de PGs

53, 106, 212

e outros

 

Potências de Base 2
e restos de divisões
por 77
             
base expoente potência divisor quociente múltiplo resto 
2         de  
          77  
2 0 1 77 0 0 1
2 1 2 77 0 0 2
2 2 4 77 0 0 4
2 3 8 77 0 0 8
2 4 16 77 0 0 16
2 5 32 77 0 0 32
2 6 64 77 0 0 64
2 7 128 77 1 77 51
2 8 256 77 3 231 25
2 9 512 77 6 462 50
2 10 1024 77 13 1001 23
2 11 2048 77 26 2002 46
2 12 4096 77 53 4081 15
2 13 8192 77 106 8162 30
2 14 16384 77 212 16324 60
2 15 32768 77 425 32725 43
2 16 65536 77 851 65527 9
2 17 131072 77 1702 131054 18
2 18 262144 77 3404 262108 36
2 19 524288 77 6808 524216 72
2 20 1048576 77 13617 1048509 67
2 21 2097152 77 27235 2097095 57
2 22 4194304 77 54471 4194267 37
2 23 8388608 77 108942 8388534 74
2 24 16777216 77 217885 16777145 71
2 25 33554432 77 435771 33554367 65
2 26 67108864 77 871543 67108811 53
2 27 134217728 77 1743087 134217699 29
2 28 268435456 77 3486174 268435398 58
2 29 536870912 77 6972349 536870873 39
2 30 1073741824 77 13944699 1073741823 1
2 31 2147483648 77 27889398 2147483646 2
2 32 4294967296 77 55778796 4294967292 4
2 33 8589934592 77 111557592 8589934584 8
2 34 17179869184 77 223115184 17179869168 16
2 35 34359738368 77 446230368 34359738336 32
2 36 68719476736 77 892460736 68719476672 64
2 37 1,37439E+11 77 1784921473 1,37439E+11 51
2 38 2,74878E+11 77 3569842947 2,74878E+11 25
2 39 5,49756E+11 77 7139685894 5,49756E+11 50
2 40 1,09951E+12 77 14279371789 1,09951E+12 23
2 41 2,19902E+12 77 28558743578 2,19902E+12 46
2 42 4,39805E+12 77 57117487157 4,39805E+12 15
2 43 8,79609E+12 77 1,14235E+11 8,79609E+12 30
2 44 1,75922E+13 77 2,2847E+11 1,75922E+13 60
2 45 3,51844E+13 77 4,5694E+11 3,51844E+13 43
2 46 7,03687E+13 77 9,1388E+11 7,03687E+13 9
2 47 1,40737E+14 77 1,82776E+12 1,40737E+14 18
2 48 2,81475E+14 77 3,65552E+12 2,81475E+14 36
2 49 5,6295E+14 77 7,31104E+12 5,6295E+14 72
2 50 1,1259E+15 77 1,46221E+13 1,1259E+15 67
2 51 2,2518E+15 77 2,92442E+13 2,2518E+15 57
2 52 4,5036E+15 77 5,84883E+13 4,5036E+15 37
2 53 9,0072E+15 77 1,16977E+14 9,0072E+15 74
2 54 1,80144E+16 77 2,33953E+14 1,80144E+16 72
2 55 3,60288E+16 77 4,67906E+14 3,60288E+16 64
2 56 7,20576E+16 77 9,35813E+14 7,20576E+16 0
2 57 1,44115E+17 77 1,87163E+15 1,44115E+17 0
2 58 2,8823E+17 77 3,74325E+15 2,8823E+17 0
2 59 5,76461E+17 77 7,4865E+15 5,76461E+17 0
2 60 1,15292E+18 77 1,4973E+16 1,15292E+18 1
             
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 3

A tabela a seguir apresenta as 11 primeiras potências de base 2 e os restos das divisões por 3.

A soma de 2 restos é 3.

3 é múltiplo de 3.

base expoente potência divisor quociente múltiplo  resto
2 de
          3  
             
2 0 1 3 0 0 1
2 1 2 3 0 0 2
2 2 4 3 1 3 1
2 3 8 3 2 6 2
2 4 16 3 5 15 1
2 5 32 3 10 30 2
2 6 64 3 21 63 1
2 7 128 3 42 126 2
2 8 256 3 85 255 1
2 9 512 3 170 510 2
2 10 1024 3 341 1023 1
             
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 9

A tabela a seguir apresenta as 13 primeiras potências de base 2 e os restos das divisões por 9.

A soma de 6 restos é 27 e é múltiplo de 9.

O expoente 5 é um número primo e corresponde ao final do intervalo.

base expoente potência divisor quociente múltiplo  resto
  de  
2 9  
             
2 0 1 9 0 0 1
2 1 2 9 0 0 2
2 2 4 9 0 0 4
2 3 8 9 0 0 8
2 4 16 9 1 9 7
2 5 32 9 3 27 5
2 6 64 9 7 63 1
2 7 128 9 14 126 2
2 8 256 9 28 252 4
2 9 512 9 56 504 8
2 10 1024 9 113 1017 7
2 11 2048 9 227 2043 5
2 12 4096 9 455 4095 1
             
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 15

A tabela a seguir apresenta as 13 primeiras potências de base 2 e os restos das divisões por 15.

A soma de 12 restos é 15 e é múltiplo de 15.

O expoente 3 é um número primo e corresponde ao final do intervalo.

Interessante observar que 15 também é a soma de potências de base 2, bem como, a soma de divisores próprios de 2^4 = 16

1 + 2 + 4 + 8 = 15

Será que estas regularidades acontecem também com outros números que são 1 unidade menor que uma potência de base 2 e restos de divisões? Com números de Mersenne, também denominados, de números quase-potências de base 2?

base expoente potência divisor quociente múltiplo  resto
  de
2 15
             
2 0 1 15 0 0 1
2 1 2 15 0 0 2
2 2 4 15 0 0 4
2 3 8 15 0 0 8
2 4 16 15 1 15 1
2 5 32 15 2 30 2
2 6 64 15 4 60 4
2 7 128 15 8 120 8
2 8 256 15 17 255 1
2 9 512 15 34 510 2
2 10 1024 15 68 1020 4
2 11 2048 15 136 2040 8
2 12 4096 15 273 4095 1
 
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 21

A tabela a seguir apresenta as 13 primeiras potências de base 2 e os restos das divisões por 21.

A soma de 12 restos é 84 e é múltiplo de 21.

O expoente 5 é um número primo e corresponde ao final do intervalo.

base expoente potência divisor quociente múltiplo  resto
  de
2 21
             
2 0 1 21 0 0 1
2 1 2 21 0 0 2
2 2 4 21 0 0 4
2 3 8 21 0 0 8
2 4 16 21 0 0 16
2 5 32 21 1 21 11
2 6 64 21 3 63 1
2 7 128 21 6 126 2
2 8 256 21 12 252 4
2 9 512 21 24 504 8
2 10 1024 21 48 1008 16
2 11 2048 21 97 2037 11
2 12 4096 21 195 4095 1
 
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 27

A tabela a seguir apresenta as 18 primeiras potências de base 2 e os restos das divisões por 27.

A soma de 18 restos é 243 e é múltiplo de 27.

O expoente 17 é um número primo e corresponde ao final do intervalo.

base expoente potência divisor quociente múltiplo  resto
2 de
          27  
             
2 0 1 27 0 0 1
2 1 2 27 0 0 2
2 2 4 27 0 0 4
2 3 8 27 0 0 8
2 4 16 27 0 0 16
2 5 32 27 1 27 5
2 6 64 27 2 54 10
2 7 128 27 4 108 20
2 8 256 27 9 243 13
2 9 512 27 18 486 26
2 10 1024 27 37 999 25
2 11 2048 27 75 2025 23
2 12 4096 27 151 4077 19
2 13 8192 27 303 8181 11
2 14 16384 27 606 16362 22
2 15 32768 27 1213 32751 17
2 16 65536 27 2427 65529 7
2 17 131072 27 4854 131058 14
2 18 262144 27 9709 262143 1
             
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 33

A tabela a seguir apresenta as 11 primeiras potências de base 2 e os restos das divisões por 33.

A soma de 10 restos é 165 e é múltiplo de 33.

O expoente 9 é múltiplo de 3 e corresponde ao final do intervalo.

base expoente potência divisor quociente múltiplo  resto
  de
2 33
             
2 0 1 33 0 0 1
2 1 2 33 0 0 2
2 2 4 33 0 0 4
2 3 8 33 0 0 8
2 4 16 33 0 0 16
2 5 32 33 0 0 32
2 6 64 33 1 33 31
2 7 128 33 3 99 29
2 8 256 33 7 231 25
2 9 512 33 15 495 17
2 10 1024 33 31 1023 1
 
www.osfantasticosnumerosprimos.com.br

Potências de base 2 e restos de divisões por 39

A tabela a seguir apresenta as 13 primeiras potências de base 2 e os restos das divisões por 39.

A soma de 12 restos é 156 e é múltiplo de 39.

O expoente 11 é um número primo e corresponde ao final do intervalo.

base expoente potência divisor quociente múltiplo  resto
2 de
  39
             
2 0 1 39 0 0 1
2 1 2 39 0 0 2
2 2 4 39 0 0 4
2 3 8 39 0 0 8
2 4 16 39 0 0 16
2 5 32 39 0 0 32
2 6 64 39 1 39 25
2 7 128 39 3 117 11
2 8 256 39 6 234 22
2 9 512 39 13 507 5
2 10 1024 39 26 1014 10
2 11 2048 39 52 2028 20
2 12 4096 39 105 4095 1
             
www.osfantasticosnumerosprimos.com.br

 

 

Autor: Ricardo Silva - maio/2025

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Veritasium em Português. Como os Computadores Quânticos Quebram a Internet… A Partir de Agora.
https://www.youtube.com/ watch?v= gzBuqxmyft8

Matérias relacionadas:

011-estudos-456-algoritmo-decomposicao-numero-fatores-primos
011-estudos-502-soma-numero-quadrado-perfeito-com-numero-quase-quadrado-perfeito
 
Livro digital (e-book)
Escada de Theon
e Sequências Numéricas
Escada de Theon e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Primos e o
Método Números Atraentes
livro Números Primos e o Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Progressões Aritméticas e Geométricas
livro digital Progressões Aritméticas e Geometricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Tabuada de Pythagoras
e Sequências Numéricas
livro digital Tabuada de Pythagoras e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Estudos de Sequências Numéricas
livro estudos de sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Os Fantásticos Números Primos
livro os fantasticos números primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Ternos Pitagóricos e Sequências Numéricas
livro Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE
o E-book
Triângulo Retângulo

 

livro Triângulo Retângulo

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos
livro descobrindo numeros primos a partir numeros compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas
livro quadrados mágicos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas
livro triangulares e sequências numéricas mágicas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo
livro quadrado mágico triplo
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Perfeitos e Sequências Numéricas
livro Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos
livro multiplicação através da soma de múltiplos
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.

curta fantasticos numeros primos no facebook
anúncio dominó tri-minox anúncio dominó quadriminox
logotipo Ric Desing

Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.

Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).

Desenvolvimento de WebSite.

Contato

ric@osfantasticosnumerosprimos.com.br

fapage dos fantasticos numeros primos
Canal youtube dos fantasticos numeros primos