Página de estudos de matemática e sequências numéricas

Descobrindo números triangulares que formam um número quadrado perfeito - 037

Número triangular é um número figurado que por meio de arranjos de pontos pode-se formar a figura de um triângulo.

Neste estudo são apresentados métodos de como descobrir números triangulares que formam números quadrados perfeitos.

Número quadrado perfeito é um número que multiplicado por ele mesmo tem resultado um número inteiro e a sua raiz quadrada também é um número inteiro.

Formando números triangulares

Através da soma de números naturais consecutivos a partir de 1 podemos obter números triangulares:

Número triangular 1

1

1 é o primeiro número triangular.

Número triangular 3

1 + 2 = 3

3 é segundo número triangular.

Número triangular 6

1 + 2 + 3 = 6

6 é terceiro número triangular.

Número triangular 10

1 + 2 + 3 + 4 = 10

10 é quarto número triangular.

Número triangular 15

1 + 2 + 3 + 4 + 5 = 15

15 é quinto número triangular.

Formando números quadrados perfeitos

Através da soma de números ímpares consecutivos podemos obter números quadrados perfeitos:

Exemplos:

1

1 + 3 = 4

1 + 3 + 5 = 9

1 + 3 + 5 + 7 = 16

3) Através da soma de dois números triangulares consecutivos podemos obter um número quadrado perfeito:

Exemplos:

1 + 3 = 4

3 + 6 = 9

6 + 10 = 16

10 + 15 = 25

Números triangulares por meio de arranjos de pontos

Através de pontos arranjados podemos representar figuras geométricas de triângulos.

Números quadrados por meio de arranjos de pontos

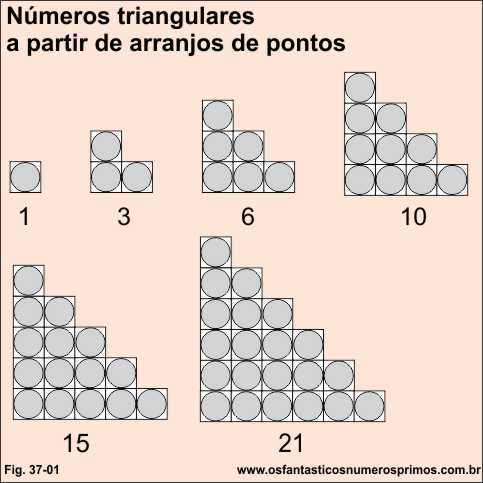
Através de pontos arranjados podemos representar figuras geométricas de quadrados.

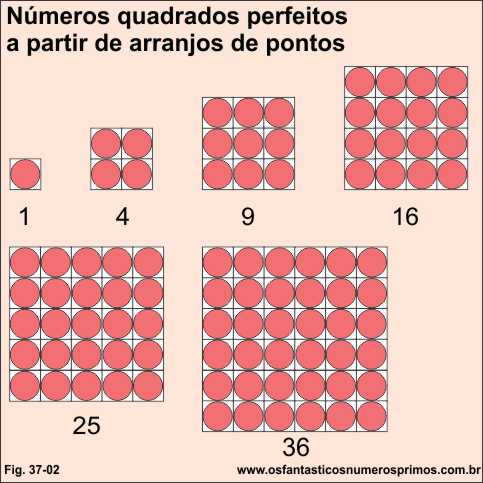
Quadrados formados pelos arranjos de dois triângulos figurados.

Tabela da soma de números triangulares

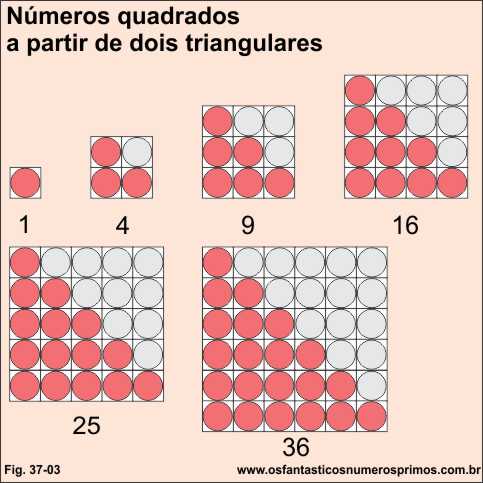
A tabela a seguir apresenta as somas de dois números triangulares consecutivos e seus respectivos números quadrados.

Observando a tabela:

a) escolha quaisquer números quadrados perfeitos;

b) subtraia a sua raiz;

c) da diferença, dividindo por 2, obtem-se o primeiro número triangular da primeira coluna;

d) da diferença, dividindo por 2 e somando a raiz quadrada, obtem-se o segundo número triangular da segunda coluna.

Método Um para se obter número quadrado perfeito

Para se saber quais números triangulares correspondem a determinado número quadrado.

O Quadrado 4

a) extraia a raiz quadrada de 4.

a raiz é 2.

b) some os números consecutivos até o 2 (1 + 2 = 3)

c) o 3 é o segundo número da parcela para obter o quadrado 4.

d) Subtraia do quadrado 4 o 3 (4 - 3 = 1).

e) O 1 é o primeiro número da parcela para obter o quadrado 4.

f) Somam-se os números 1 e 3 (1 + 3 = 4).

g) os números triangulares 1 e 3 são os que formam o quadrado 4

O quadrado 9

a) extraia a raiz quadrada de 9.

a raiz é 3.

b) some os números consecutivos até 3 (1 + 2 + 3 = 6)

c) o 6 é o segundo número triangular da parcela para obter o quadrado 9

d) subtraia do quadrado 9 o 6 (9 - 6 = 3)

e) o 3 é primeiro número triangular da parcela para obter o quadrado 9

f) somam-se o números 3 e 6 (3 + 6 = 9)

g) os números triangulares 3 e 6 são os que formam o quadrado 9.

Método Dois para descobrir número quadrado perfeito

Para se saber quais números triangulares correspondem a determinado número quadrado.

O quadrado 25

a) extraia a raiz de 25.

a raiz é 5.

b) subtraia do quadrado a sua raiz quadrada (25 - 5 = 20)

c) divida o resultado 20 por 2 (20 : 2 = 10).

d) O número 10 é o primeiro triangular da parcela para obter o quadrado 25.

e) some o 10 com a raiz 5 (10 + 5 = 15)

f) O número 15 é o segundo triangular da parcela para obter o quadrado 25.

g) somam-se os números 10 e 15 (10 + 15 = 25).

h) os números triangulares 10 e 15 são os que formam o quadrado 25.

O quadrado 64

a) extraia a raiz de 64.

a raiz é 8.

b) subtraia do quadrado a sua raiz quadrada(64 - 8 = 56)

c) divida o resultado 56 por 2 (56 : 2 = 28)

d) o número 28 é o primeiro triangular da parcela para obter o quadrado 64.

e) some o 28 com a raiz 8 (28 + 8 = 36).

f) o número 36 é o segundo triangular da parcela para obter o quadrado 64.

g) somam-se os números 28 e 36 (28 + 36 = 64).

h) os números triangulares 28 e 36 são os que formam o quadrado 64.

O quadrado 441

a) extraia a raiz de 441 - a raiz é 21

b) subtraia do quadrado a sua raiz quadrada (441-21=420)

c) divida o resultado 420 por 2 (420 : 2 = 210)

d) o número 210 é o primeiro triangular da parcela para obter o quadrado 64

e) some o 210 com a raiz 21 (210 + 21 = 231).

f) o número 231 é o segundo triangular da parcela para obter o quadrado 441

g) somam-se os números 210 e 231 (210 + 231 = 441)

h) os números triangulares 210 e 231 são os formam o quadrado 441.

Autor: Ricardo Silva

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-003-soma-numeros-consecutivos

011-estudos-004-soma-numeros-triangulares

Livro digital (e-book)
Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

---

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.