


Revendo o vídeo da OBEMEP 2006 - ESTÁGIO DOS PROFESSORES PREMIADOS - PALESTRA: O NÚMERO DE OURO - PROFESSOR MICHEL SPIRA, vídeo este publicado no Canal do Youtube: Conteúdo Digitais, postado em 2011.
Na Palestra, o Professor Michel Spira apresenta vários exemplos com equações algébricas e modelos matemáticos onde ocorrem O Número de Ouro, Secção de Ouro, Número Dourado.
Um detalhe me chamou a atenção, aos 42 minutos da palestra, o Professor apresenta um modelo matemático com um triângulo inscrito em um retângulo arbitrário:
a) desenha-se um retângulo de medidas quaisquer;
b) o triângulo tem que estar com um dos vértices em um dos vértices do retângulo;
c) os dois outros vértices do triângulo tem que estar: um na base e o outro na lateral do retângulo;
d) aparecem mais três novos triângulos e a pergunta é: Quando os três novos triângulos têm as mesmas áreas?
O Professor dá a seguinte resposta: "Os três novos triângulos terão as mesmas áreas quando dois vértices do triângulo inscrito estiverem no ponto áureo da base e no ponto áureo da lateral do retângulo".
Então fiz alguns modelos matemáticos para comprovar se um triângulo inscrito em um retângulo, criam três novos triângulos de mesmas áreas.
Na construção do modelo-1, originam-se dois novos triângulos com a metade da área do triângulo inscrito.
Juntando-se o dois novos triângulos, formamos um triângulo de mesma área que o triângulo inscrito.
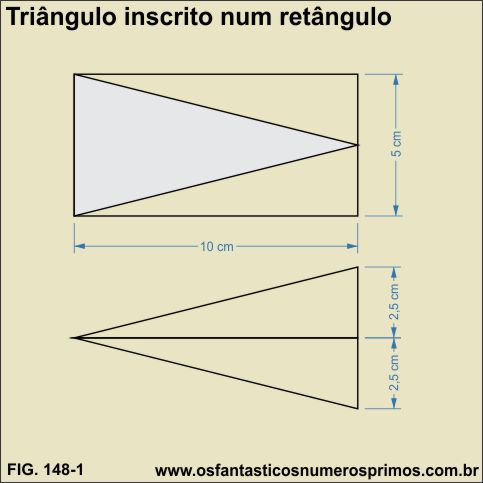
Na construção do modelo-2, originam-se dois novos triângulos com a metade da área do triângulo inscrito.
Juntando-se o dois triângulos, formamos um triângulo de mesma área que o triângulo inscrito.
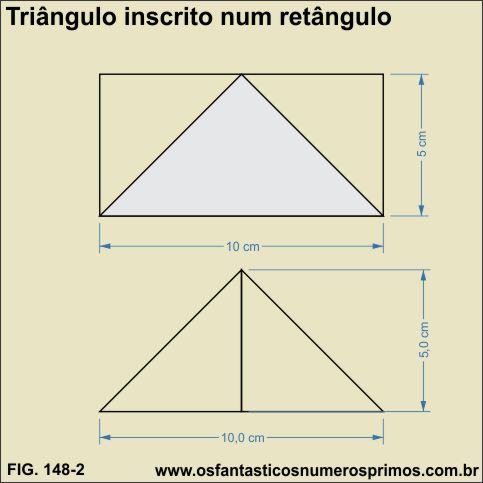
Na construção do modelo-3, um dos vértices do triângulo inscrito parte de um dos vértice do retângulo.
O segundo vértice do triângulo está sobre o ponto médio da base do retângulo.
O terceiro vértice do triângulo está sobre o ponto médio da lateral direta do retângulo.
Originam-se três novo triângulos: 1, 2 e 3, os quais, só dois têm as mesmas áreas.
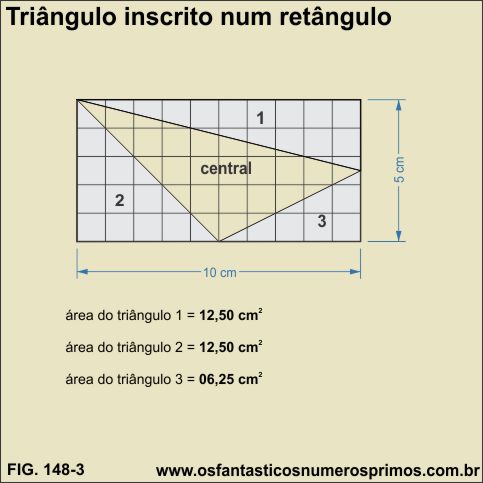
Na construção do modelo-4, um dos vértices do triângulo inscrito parte de um dos vértice do retângulo.
O segundo vértice do triângulo está sobre 1/4 da base do retângulo.
O terceiro vértice do triângulo está sobre 1/4 da lateral direta do retângulo.
Originam-se três novos triângulos: 1, 2 e 3 de áreas diferentes.
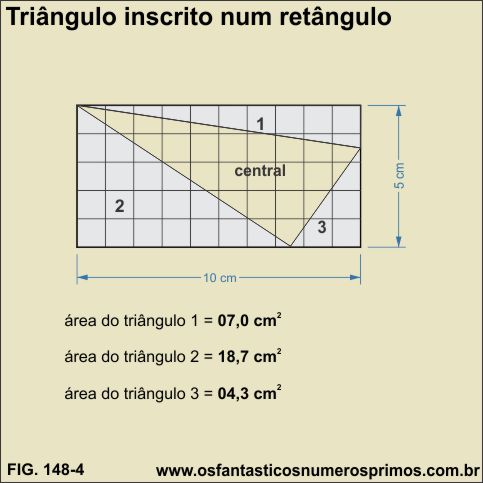
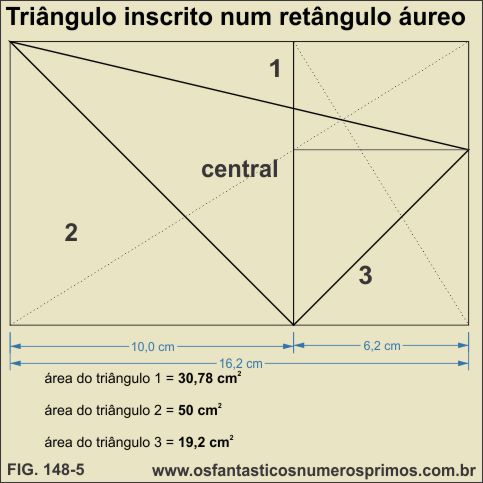
Na construção do modelo - 5, desenhou-se um retângulo áureo a partir de um quadrado de lado de 10 cm.
Um dos vértices do triângulo inscrito parte de um dos vértice do retângulo.
O segundo vértice do triângulo está sobre o ponto áureo da base do retângulo.
O terceiro vértice do triângulo está sobre o ponto áreo da lateral direta do retângulo.
Originam-se três novo triângulos: 1, 2 e 3 de áreas diferentes.
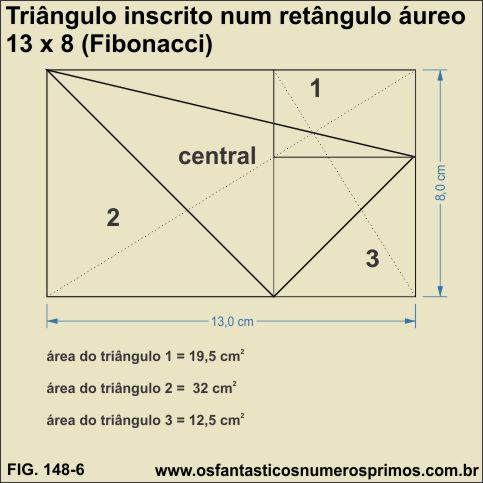
Na construção do modelo - 6, desenhou-se um retângulo áureo com as medidas 13 cm x 8 cm (Sequência de Fibonacci) a partir de um quadrado de lado de 8 cm.
Um dos vértices do triângulo inscrito parte de um dos vértice do retângulo.
O segundo vértice do triângulo está sobre o ponto áureo da base do retângulo.
O terceiro vértice do triângulo está sobre o ponto áreo da lateral direta do retângulo.
Originam-se três novo triângulos: 1, 2 e 3 de áreas diferentes.
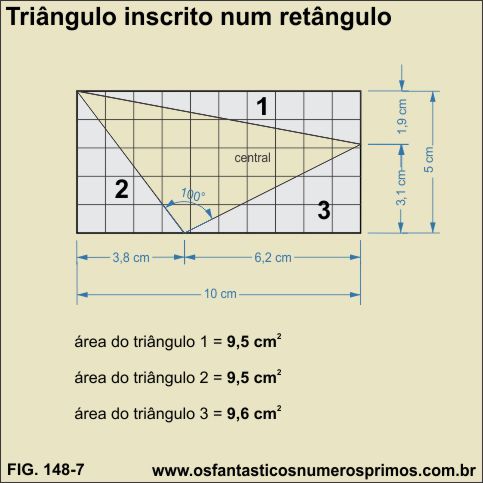
Na construção do modelo-7, desenhou-se um retângulo com as medidas 10 cm x 5 cm.
Dividiu-se tanto o comprimento e a largura por 1,6 e marcando-se os pontos áureos.
Um dos vértices do triângulo inscrito parte de um dos vértice do retângulo.
O segundo vértice do triângulo está sobre o ponto áureo da base do retângulo.
Observação: a medida de 3,8 cm parte do vértice esquerdo inferior do retângulo.
O terceiro vértice do triângulo está sobre o ponto áreo da lateral direta do retângulo.
Originaram-se três novos triângulos: 1 e 2 com área iguais e o 3 com 0,1 de diferença.
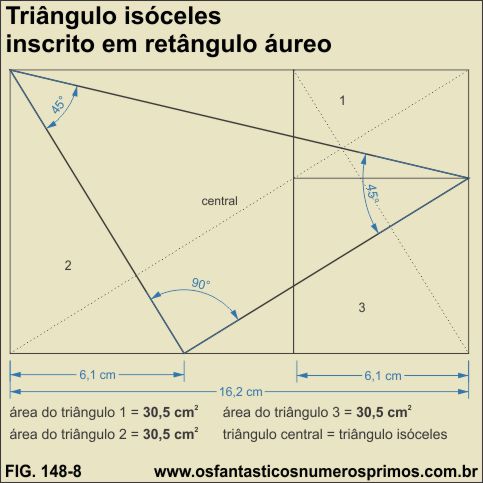
Na construção do modelo - 8, desenhou-se um retângulo áureo a partir de um quadrado de lado de 10 cm.
Um dos vértices do triângulo inscrito parte de um dos vértice do retângulo.
O segundo vértice do triângulo está sobre o ponto áureo da base do retângulo
Observação: a medida de 6,1 cm parte do vertice esquerdo inferior do retângulo.
O terceiro vértice do triângulo está sobre o ponto áureo da lateral direta do retângulo.
Originaram-se três novos triângulos: 1, 2 e 3 de áreas iguais.
O triângulo central é um triângulo retângulo isóceles.
Autor: Ricardo Silva - novembro/2017
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato