


O presente estudo faz demonstrações de construções geométricas de divisões de um quadrado de onde se originam dinamicamente novos quadrados e novos triângulos retângulos e também de triângulos áureos inscritos em um quadrado formando pontos de intersecções e eixos de simetrias formando novos quadrados e novos triângulos áureos.
A partir de um quadrado e traçando-se:
a) uma diagonal, obtem-se dois triângulos retângulos isóceles;
b) duas diagonais, obtem-se quatro triângulos retângulos isóceles;
c) seguimentos a partir dos pontos médios, obtemos novos quadrados e triângulos retângulos isóceles;
d) seguimentos de um ponto médio a um vértice de qualquer oitava parte do quadrado obtêm-se outros triângulos retângulos isóceles.
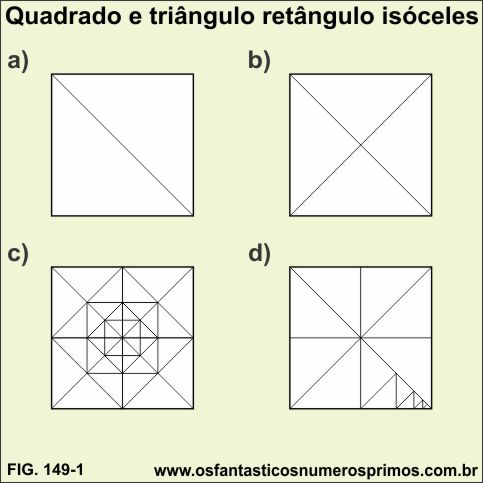
Interessante observar nesta construção geométrica é que temos duas séries de quadrados; uns que vão diminuindo em relação a largura e outros em relação a diagonal na proporção de 1:2 e que também se originam novos triângulos retângulos isóceles.
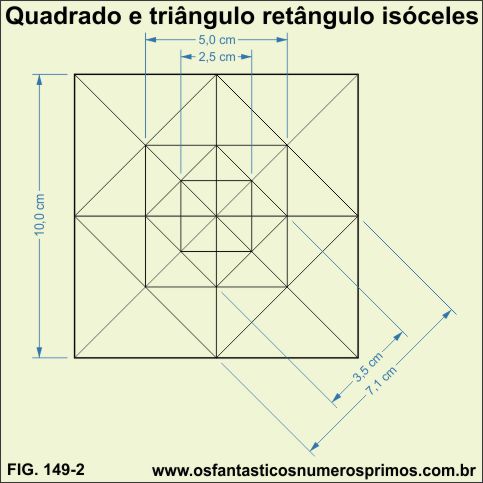
A área do quadrado inscrito em um triângulo retângulo isóceles corresponde a metade da área de um triângulo retângulo isóceles originado de um quadrado.
a) área do triângulo retângulo isóceles
10 x 10 = 100
100 : 2 = 50
b) área do quadrado incrito
5 x 5 = 25

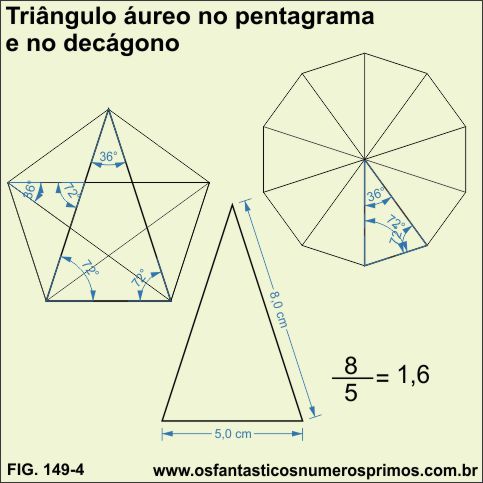
Triângulo Áureo, também chamado de Triângulo de Ouro, Triângulo Dourado ou Triângulo Sublime aparece naturalmente no pentagrama; estrela de cinco pontas quando desenhada a partir de um pentágono e também no decágono.
O Triângulo Áureo possui dois ângulos de 72 graus e um de 36 graus e o comprimento do lado dividido pela sua base tem como resultado, um número próximo ao número áureo: 1,618.
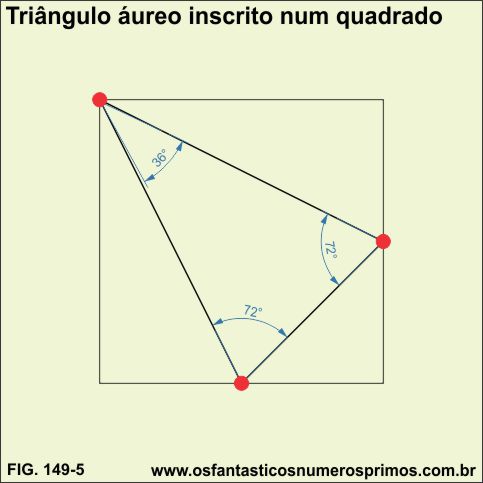
Pode-se inscrever um Triângulo Áureo em um quadrado da seguine forma:
a) marca-se o ponto médio da base e da lateral direita ou esqueda do quadrado;
b) traçam-se três seguimentos; do vértice superior esquerdo ao ponto médio da base, do vértice superior esquerdo ao ponto médio da lateral direita e outro seguimento ligando o ponto médio da base ao ponto médio da lateral direita.
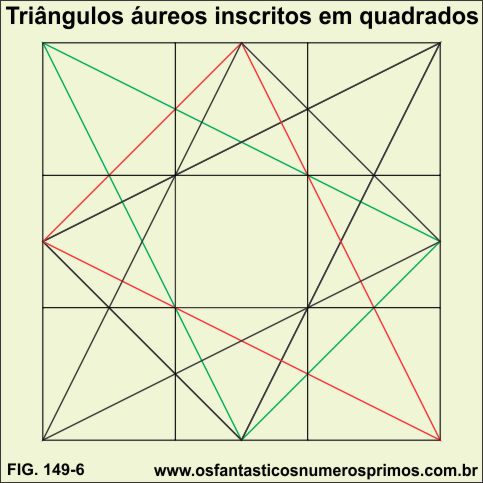
Inscrevendo-se 4 triângulos áureos em um quadrado, criam-se pontos de intesecções nos quais são possíveis passarem duas linhas paralelas horizontais e duas linhas paralelas verticais, de modo que obtem-se mais 9 pequenos quadrados com as seguintes características:
a) os quadrados dos vértices possuem um triângulo áureo inscrito;
b) os quadrados dos meios possuem dois triângulos áureos inscritos;
c) o quadrado central não possui nenhum triângulo áureo inscrito.
Nesta construção, nota-se uma belíssima simetria geométrica, entre pontos, ângulos, linhas e figuras formando um perfeito equilíbrio.
Autor: Ricardo Silva - novembro/2017
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato