


Diagonais de um polígono são segmentos de retas cujas extremidades tocam dois vértices não consecutivos desse polígono.
Polígono é um contorno formado por segmentos de retas que nâo se cruzam.
O triângulo não possui diagonais.
O pentágono é o único polígono cujo número de diagonais é o mesmo de vértices e de lados.
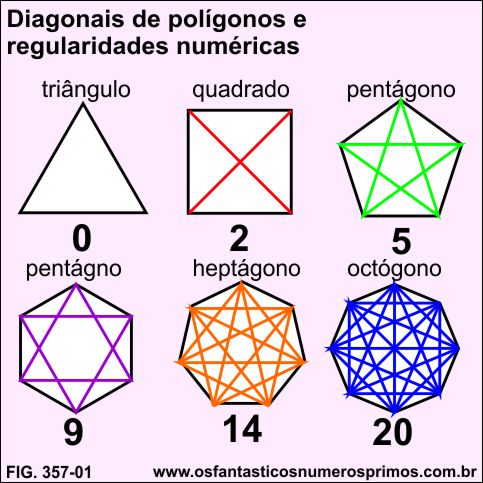
O presente estudo demonstra novas regularidades numéricas relacionadas a polígonos regulares de lados ímpares e suas diagonais.
As diagonais que partem de cada vértice de polígonos regulares formam uma progressão aritmética: 1, 2, 3, 4,... de forma que podemos relacionar cada polígono com determinada posição:
Exemplos:
a) no quadrilátero, de cada vértice parte 1 diagonal, portanto o quadrilátero tem a ordem / posição de número 1;
b) no pentágono, de cada vértice partem 2 diagonais, portanto o pentágono tem a ordem / posição de número 2;
c) no hexágono, de cada vértice partem 3 diagonais, portanto o hexágono tem a ordem / posição de número 3;
A tabela a seguir apresenta os 20 primeiros polígonos regulares com suas respectivas quantidades de lados/vértices e diagonais.
Interessante observar que polígonos de ordem / posição par, a quantidade de lados / vértices estão estritamente relacionados com a quantidade de diagonais:
O pentágono têm 5 lados/vertices e 5 diagonais.
A quantidade de diagonais é múltiplo dos lados/vértices.
O heptágono têm 7 lados/vertices e 14 diagonais.
A quantidade de diagonais é múltiplo dos lados/vértices.
A quantidade de diagonais é o dobro da quantidade de lados/vertices.
O eneágono têm 9 lados/vertices e 27 diagonais.
A quantidade de diagonais é múltiplo dos lados/vértices.
A quantidade de diagonais é o triplo da quantidade de lados/vertices.
O undecágono têm 11 lados/vertices e 44 diagonais.
A quantidade de diagonais é múltiplo dos lados/vértices.
A quantidade de diagonais é o quádruplo da quantidade de lados/vertices...
...e assim sucessivamente...
Nos polígonos de ordem / posição ímpar, não há esta regularidade numérica, pois a quantidade de diagonais não são múltiplos de lados/vértices.
| Polígonos: | ||||
|---|---|---|---|---|
| vértices e diagonais | ||||
| diagonais | ||||
| que | ||||
| partem | Quant. | diferença | ||
| nome | lados / | de cada | de | diagonais |
| vértices | vértice | diagonais | ||
| quadrilátero | 4 | 1 | 2 | |
| 3 | ||||
| pentágono | 5 | 2 | 5 | |
| 4 | ||||
| hexágono | 6 | 3 | 9 | |
| 5 | ||||
| heptágono | 7 | 4 | 14 | |
| 6 | ||||
| octógono | 8 | 5 | 20 | |
| 7 | ||||
| eneágono | 9 | 6 | 27 | |
| 8 | ||||
| decágono | 10 | 7 | 35 | |
| 9 | ||||
| undecágono | 11 | 8 | 44 | |
| 10 | ||||
| dodecágono | 12 | 9 | 54 | |
| 11 | ||||
| tridecágono | 13 | 10 | 65 | |
| 12 | ||||
| tetradecágono | 14 | 11 | 77 | |
| 13 | ||||
| pentadecágono | 15 | 12 | 90 | |
| 14 | ||||
| hexadecágono | 16 | 13 | 104 | |
| 15 | ||||
| heptadecágono | 17 | 14 | 119 | |
| 16 | ||||
| octadecágono | 18 | 15 | 135 | |
| 17 | ||||
| eneadecágono | 19 | 16 | 152 | |
| 18 | ||||
| icoságono | 20 | 17 | 170 | |
| www.osfantasticosnumerosprimos.com.br | ||||
Conforme regularidades numéricas descritas acima, podemos deduzir fórmulas para se determinar a quantidade de diagonais de polígonos de lados/vértices ímpares:
Exemplo 1)
a) determinando o pentágono - (2n+3)
(2n + 3) =
2 x 1 + 3
2 + 3 = 5 (polígono de 5 lados/vértices)
b) determinando a quantidade de diagonais - n(2n+3)
1 x 5 = 5
Exemplo 2)
a) determinando o heptágono - (2n+3)
(2n + 3) =
2 x 2 + 3
4 + 3 = 7 (polígono de 7 lados/vértices)
b) determinando a quantidade de diagonais - n(2n+3)
2 x 7 = 14
Exemplo 3)
a) determinado o eneágono - (2n+3)
(2n + 3) =
2 x 3 + 3
6 + 3 = 9 (polígono de 9 lados/vértices)
b) determinando a quantidade de diagonais - n(2n+3)
3 x 9 = 27
Autor: Ricardo Silva - dezembro/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato