


O presente estudo apresenta um novo padrão e regularidades numéricas relacionados a soma de lados de polígonos com suas diagonais com a sequência de números triangulares.
Polígono é um contorno formado por segmentos de reta que não se cruzam e conforme o números de lados, os polígonos possuem nomes especiais, tais como: triângulo - polígono de 3 lados; quadrilátero - polígono de 4 lados; pentágono - polígono de 5 lados, etc.
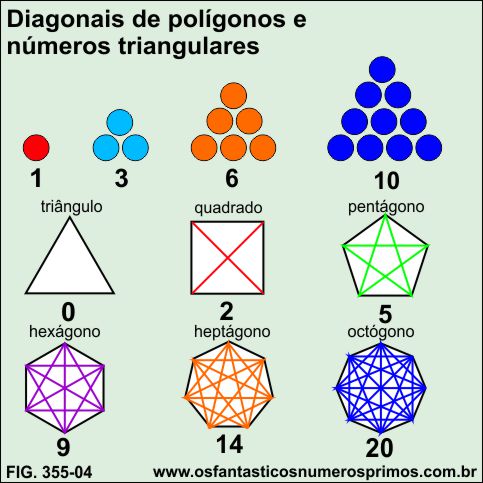
A diagonal de um polígono é o segmento de reta cujas extremidades tocam em dois vértices desse polígono.
O triângulo não possui diagonais e o pentágono é o único polígono cujas quantidades de diagonais é a mesma do números de lados e de vértices.
Para sabermos a quantidade de diagonais que um determinado polígono tem, podemos utilizar a fórmula que determina o total de diagonais de um polígono:
| n x ( n - 3 ) | |
| d = | _______ |
| 2 |
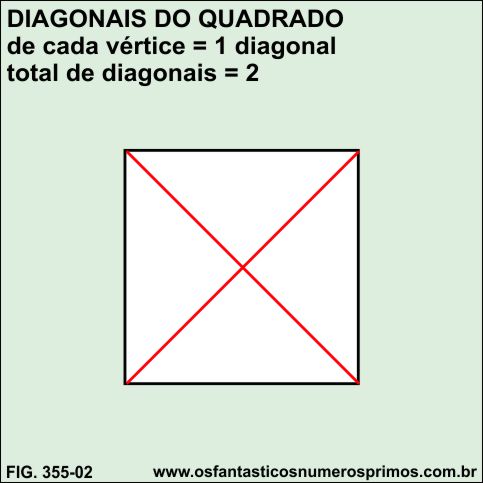
Quadrilátero (Quadrado) - 4 lados ( n = 4 )
( 4 - 3 ) = 1
de cada vértice parte 1 diagonal.
n x ( n - 3 ) d = _______ 2
4 x ( 4 - 3 ) d = _______ 2
4 x (1) d = _______ 2
4 x 1 d = _______ 2
4 d = _______ 2
d = 2 Número de diagonais: 2
Números triangulares
Números triangulares, também denominados de números figurados, números geométricos, são números formados por meio de arranjos de pontos, os quais se podem formar figuras geométricas de triângulos
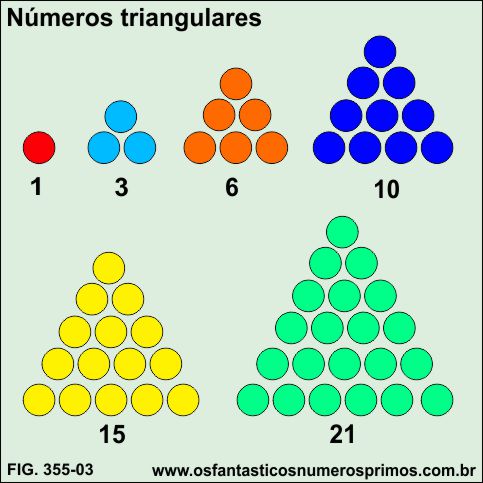
Números triangulares podem ser obtidos através:
a) da soma de números consecutivos.
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
d) da fórmula
n x ( n + 1) _______ 2 e também por meio de outros métodos publicados em matérias aqui no WebSite Os Fantásticos Números Primos bem como no livro digital Números Triangulares de Sequêncicas Numéricas.
Diagonais de polígonos e regularidades numéricas
A tabela a seguir apresenta os 49 primeiros polígonos, relacionando os lados com suas respectivas quantidades de diagonais.
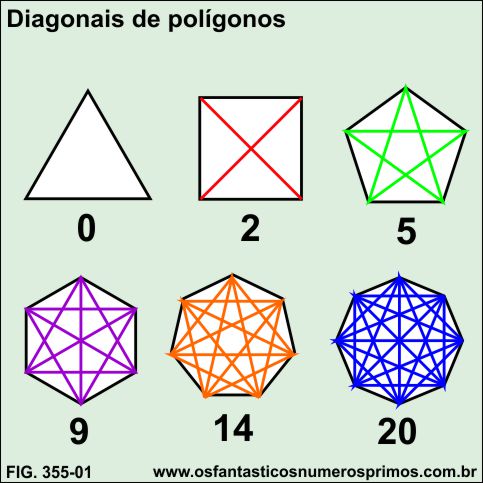
Dispondo sequencialmente os polígonos e posteriormente somando os seus lados com a quantidade de suas diagonais obtem-se a sequência de números triangulares a partir do segundo número triângular: 3, 6, 10, 15, 21, 28, 36, 45, 55, 66,...
Polígonos: lados e diagonais e números triângulares Quant. de Números Ordem Polígonos Lados Diagonais Triân- -gulares 1 - - - - 2 triângulo 3 0 3 3 quadrilátero 4 2 6 4 pentágono 5 5 10 5 hexágono 6 9 15 6 heptágono 7 14 21 7 octógono 8 20 28 8 eneágono 9 27 36 9 decágono 10 35 45 10 undecágono 11 44 55 11 dodecágono 12 54 66 12 tridecágono 13 65 78 13 tetradecágono 14 77 91 14 pentadecágono 15 90 105 15 hexadecágono 16 104 120 16 heptadecágono 17 119 136 17 octadecágono 18 135 153 18 eneadecágono 19 152 171 19 icoságono 20 170 190 20 21 189 210 21 22 209 231 22 23 230 253 23 24 252 276 24 25 275 300 25 26 299 325 26 27 324 351 27 28 350 378 28 29 377 406 29 30 405 435 30 31 434 465 31 32 464 496 32 33 495 528 33 34 527 561 34 35 560 595 35 36 594 630 36 37 629 666 37 38 665 703 38 39 702 741 39 40 740 780 40 41 779 820 41 42 819 861 42 43 860 903 43 44 902 946 44 45 945 990 45 46 989 1035 46 47 1034 1081 47 48 1080 1128 48 49 1127 1176 49 50 1175 1225 50 51 1224 1275 www.osfantasticosnumerosprimos.com.br Números triangulares e diagonais de polígonos - método 1
A partir de números triangulares é possível determinar a quantidade de diagonais de um polígono, procedendo-se da seguinte forma:
Determinando as diagonais do quadrado com números triangulares
a) multiplica-se os dois números consecutivos 3 x 4 (refere-se ao quadrilátero de 4 lados);
b) produto = 12 (número oblongo);
c) número oblongo dividido por 2 tem como resultado um número triangular
12 : 2 = 6 (6 é terceiro número triangular);
d) Subtrái-se 4 (quadrilátero) do triangular 6;
6 - 4 = 2
e) a diferença 2 é a quantidade de diagonais do quadrado.
Determinando as diagonais do pentágono com números triangulares
a) multiplica-se os dois números consecutivos 4 x 5 (refere-se ao pentágono);
b) produto = 20 (número oblongo);
c) número oblongo dividido por 2 tem como resultado um número triangular;
20 : 2 = 10 (10 é quarto número triangular)
d) Subtrái-se 5 (pentágono) do triangular 10;
10 - 5 = 5
e) a diferença 5 é a quantidade de diagonais do pentágono.
Números triangulares e diagonais de polígonos - método 2
Subtraindo 1 unidade de números triangulares a partir do número triangular 3, obtêm-se quantidades de diagonais de polígonos regulares.
Vejamos:
Diagonais do quadrado
O produto de dois números consecutivos dividido por 2 e posteriormente subtraído 1 unidade tem como resultado o número de diagonais do polígono regular cujas quantidades de lados é antecessor do segundo fator da multiplicação de dois números consecutivos.
(2 x 3) / 2 = 3
O segundo fator da multiplicação é 3.
3 é o antecessor de 4 (polígono de 4 lados).
Triangular 3 subtraído 1 unidade.
3 - 1 = 2
2 é quantidade de diagonais do quadrado.
Diagonais do pentágono
O produto de dois números consecutivos dividido por 2 e posteriormente subtraído 1 unidade tem como resultado o número de diagonais do polígono regular cujas quantidades de lados é antecessor do segundo fator da multiplicação de dois consecutivos.
(3 x 4) / 2 = 6
O segundo fator da multiplicação é 4.
4 é o antecessor de 5 (polígono de 5 lados).
Triangular 6 subtraído 1 unidade.
6 - 1 = 5
5 é quantidade de diagonais do pentágono.
Diagonais do hexágono
O produto de dois números consecutivos dividido por 2 e posteriormente subtraído 1 unidade tem como resultado o número de diagonais do polígono regular cujas quantidades de lados é antecessor do segundo fator da multiplicação de dois consecutivos.
(4 x 5) / 2 = 10
O segundo fator da multiplicação é 5.
5 é o antecessor de 6 (polígono de 6 lados).
Triangular 10 subtraído 1 unidade.
10 - 1 = 9
9 é quantidade de diagonais do hexágono.
Autor: Ricardo Silva - dezembro/2021
Fontes Bibliográficas:
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Matérias relacionadas:
011-estudos-100-triangulo-equilatero-sequencias-numericas
011-estudos-101-o-quadrado-sequencias-numericas
011-estudos-119-diagonais-de-poligonos-e-sequencias-numericas
Livro digital (e-book)
Tabuada de Pythagoras
e Sequências Numéricas

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
RECEBAM GRATUITAMENTE
O E-BOOK
TRIÂNGULO RETÂNGULO:

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
L A N Ç A M E N T O ! ! !

NOVO LIVRO DIGITAL:
LIVRO DIGITAL (E-book) Números Triangulares e Sequências Numéricas

Mais informações, acesse:
Manual Digital (E-book) Quadrado Mágico Triplo

LIVRO GRATUITO
Mais informações, acesse:
Livro digital (e-book)
Números Perfeitos e Sequências Numéricas

Mais informações, acesse:
Manual Digital (E-book) Multiplicação através da soma de múltiplos

LIVRO GRATUITO
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato