


Nós brasileiros, assim como outros povos, cujos alfabetos derivam da Língua Latina que era falada pelos romanos, escrevemos da esquerda para à direita, enquanto outros povos tem o costume de esqueverem da direita para à esquerda.
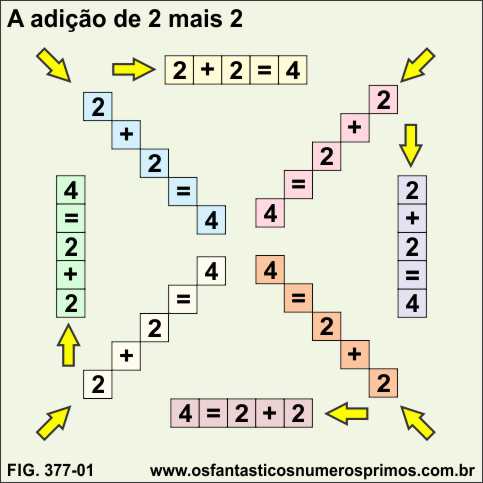
De quantas maneiras, por exemplo, poderíamos efetuar a operação de adição: 2 + 2 = 4, veja que já estou escrevendo da esquerda para à direita.
Será que teríamos, dezenas, centenas ou milhares de possibilidades?
Quadrados Mágicos são dispositivos numéricos formados por matrizes quadriculadas cujas quantidades são em números quadrados perfeitos: 9 (3 x 3) , 16 (4 x 4), 25 (5 x 5), 36 (6 x 6), 49 (7 x 7),... etc..., nas quais são dispostas em certa ordem, sequências numéricas finitas formadas por:
a) progressões aritméticas (P.A.s) em que a soma das linhas, colunas e diagonais apresentam a mesma soma, denominada de Constante Mágica;
b) progressões geométricas (P.G.s) em que o produto dos números nas células das linhas, colunas e diagonais apresentam o mesmo valor;
c) sequências numéricas que não são nem P.As e nem P.Gs em que o produto dos números nas células das linhas, colunas e diagonais apresentam o mesmo valor;
Podem ser formados 362.880 (1! x 2! x 3! x 4! x 5! x 6! x 7! x 8! x 9!) combinações com o quadrado de ordem 3 (3 x 3) de 9 células, mas somente 8 combinações formam Quadrados Mágicos.
| Quantidade de Combinações | |
|---|---|
| de Quadrados Mágicos | |
| Ordem | Quantidade |
| 3 | 8 |
| 4 | 880 |
| 5 | 275.305.224 |
| 6 | estima-se 1,7 x 10 19 |
Fonte: Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p.
As análises a seguir do Quadrado Mágico 6x6 de Constante Mágica: 111 e Soma do Quadrado: 666 e de suas derivações foram extraídas do artigo do Professor Vernon Jenkins: WISDOM’S KEY: An examination of 666 as a number per se do WebSite: www.whatabeginning.com.
O Professor Vernon Jenkins era um Matemático e publicou estudos em que relaciona as Escrituras Sagradas com sequências numéricas como: números primos, números triangulares, bem como geometria.
Lendo o artigo do Professor Vernon Jenkins e observando atentamente o Quadrado Mágico 6x6, percebe-se algo diferente em sua construção, isto porque, o Professor conseguiu derivar:
a) 1 Quadrado Mágico 6x6 Imperfeito ao Quadrado cujas somas das linhas horizontais são iguais;
b) 1 Quadrado Mágico 6x6 Imperfeito Triangular cujas somas das linhas horizontais são iguais;
c) 4 séries de Quadrados multiplicados pelo Quadrado Mágico 6x6 em que a soma total de cada quadrado derivado apresentam a mesma soma.
E o mais intrigante ainda é que reconstruindo o Quadrado Mágico 6x6 do Professor Vernon com os métodos divulgados aqui no WebSite Os Fantásticos Números Primos, não se obteve sucesso, isto é, não se conseguiu manter as mesmas posições dos números em suas células originais.
O mesmo aconteceu com as derivações de quadrados mágicos que o Professor Vernon realizou, também não foram possíveis de reconstruí-las com outros métodos de construções de quadrados mágicos de forma que tivessem as mesmas somas de linhas, colunas e diagonais.
Neste caso, se conseguiu ter a mesma soma total de cada quadrado.
Quadrados Mágicos 6x6 reconstruídos com os Métodos de La Hire, La Loubère, Lux com a sequência dos números naturais de 1 a 36 apresentam as mesmas constantes mágicas e somas dos quadrados idênticas a do Professor Vernon.
| Quadrado Mágico 6x6 | |||||||
| Constante Mágica 111 | |||||||
| Soma do quadrado 666 | |||||||
| 111 | |||||||
| 8 | 30 | 26 | 22 | 24 | 1 | = | 111 |
| 2 | 34 | 18 | 28 | 12 | 17 | = | 111 |
| 7 | 20 | 3 | 29 | 31 | 21 | = | 111 |
| 25 | 4 | 23 | 15 | 9 | 35 | = | 111 |
| 36 | 13 | 27 | 11 | 19 | 5 | = | 111 |
| 33 | 10 | 14 | 6 | 16 | 32 | = | 111 |
| = | = | = | = | = | = | ||
| 111 | 111 | 111 | 111 | 111 | 111 | 111 | |
Fonte: adaptado de: Jenkins, Vernon. WISDOM’S KEY: An examination of 666 as a number per se - www.whata
No Quadrado Mágico 6x6 imperfeito ao Quadrado, o Professor Vernon consegue uma proeza, pois a soma de cada linha horizontal apresenta uma mesma constante que é 2.701 e a soma total 16.206.
Quadrados Mágicos Perfeitos ao Quadrado são quadrados raros de serem contruídos e aqui se tem um quadrado mágico imperfeito ao quadrado em que a soma de cada linha horizontal tem uma mesma constante mágica.
Até o presente momento, nâo se conseguiu construir quadrado mágico 3x3 perfeito ao quadrado, como também quadrado mágico 6x6 perfeito ao quadrado e de outras ordens.
Quadrados Mágicos 6x6 reconstruídos com os Métodos de La Hire, La Loubère, Lux com a sequência dos números quadrados de 1 a 1296 e com a configuração do quadrado do Professor Vernon não apresentaram as mesmas somas das linhas, mas sim a soma total de 16.206.
| Quadrado Mágico 6x6 | |||||||
| imperfeito | |||||||
| ao quadrado | |||||||
| 2773 | |||||||
| 64 | 900 | 676 | 484 | 576 | 1 | = | 2701 |
| 4 | 1156 | 324 | 784 | 144 | 289 | = | 2701 |
| 49 | 400 | 9 | 841 | 961 | 441 | = | 2701 |
| 625 | 16 | 529 | 225 | 81 | 1225 | = | 2701 |
| 1296 | 169 | 729 | 121 | 361 | 25 | = | 2701 |
| 1089 | 100 | 196 | 36 | 256 | 1024 | = | 2701 |
| = | = | = | = | = | = | ||
| 3127 | 2741 | 2463 | 2491 | 2379 | 3005 | 2839 | |
Fonte: adaptado de: Jenkins, Vernon. WISDOM’S KEY: An examination of 666 as a number per se - www.whata
Utilizando a disposição dos números do Quadrado Mágico 6x6 em relação a ordem / posição, o Professor Vernon construiu outro quadrado permutando os números para números triangulares de 1 a 666, conseguindo outra proeza, pois a soma de cada linha horizontal do quadrado tem o mesmo resultado que é 1.406 e soma total 8.436.
Quadrados Mágicos 6x6 reconstruídos com os Métodos de La Hire, La Loubère, Lux com a sequência dos números triangulares de 1 a 666 e com a configuração de ordem / posição do quadrado do Professor Vernon não apresentaram as mesmas somas das linhas horizontais, mas sim a soma total 8.436.
| Quadrado Mágico 6x6 | |||||||
| imperfeito | |||||||
| triangular | |||||||
| 1442 | |||||||
| 36 | 465 | 351 | 253 | 300 | 1 | = | 1406 |
| 3 | 595 | 171 | 406 | 78 | 153 | = | 1406 |
| 28 | 210 | 6 | 435 | 496 | 231 | = | 1406 |
| 325 | 10 | 276 | 120 | 45 | 630 | = | 1406 |
| 666 | 91 | 378 | 66 | 190 | 15 | = | 1406 |
| 561 | 55 | 105 | 21 | 136 | 528 | = | 1406 |
| = | = | = | = | = | = | ||
| 1619 | 1426 | 1287 | 1301 | 1245 | 1558 | 1475 | |
Fonte: adaptado de: Jenkins, Vernon. WISDOM’S KEY: An examination of 666 as a number per se - www.whata
Utilizando como base o Quadrado Mágico 6x6 de Constante Mágica 111, o Professor Vernon fez 4 cópias, numerou as células dos quadrados de 1 a 36 conforme a figura 377-02 (números em vermelho). Multiplicou cada número de cada célula de cada quadrado mágico pelo número correspondente na cor vermelha, produzindo desta forma 4 novos quadrados mágicos imperfeitos.

Fonte: Jenkins, Vernon. WISDOM’S KEY: An examination of 666 as a number per se - www.whata
Os 4 quadrados mágicos imperfeitos gerados apresentam a mesma soma total de 12.321 que corresponde ao número quadrado perfeito de 111, que é a Constante Mágica do Quadrado Mágico 6x6 utilizado como base.
Quadrados Mágicos 6x6 reconstruídos com os Métodos de La Hire, La Loubère, Lux com a sequência dos números de 1 a 36, com 4 cópias de cada quadrado e seguindo as etapas descrita acima apresentaram a mesma Soma Total de 12.321.
As linhas, colunas e diagonais não apresentam Constante Mágica.
Soma total 12.321.
| 2446 | |||||||
| 8 | 60 | 78 | 88 | 120 | 6 | = | 360 |
| 14 | 272 | 162 | 280 | 132 | 204 | = | 1064 |
| 91 | 280 | 45 | 464 | 527 | 378 | = | 1785 |
| 475 | 80 | 483 | 330 | 207 | 840 | = | 2415 |
| 900 | 338 | 729 | 308 | 551 | 150 | = | 2976 |
| 1023 | 320 | 462 | 204 | 560 | 1152 | = | 3721 |
| = | = | = | = | = | = | ||
| 2511 | 1350 | 1959 | 1674 | 2097 | 2730 | 2358 |
As linhas, colunas e diagonais não apresentam Constante Mágica.
Soma total 12.321.
| 2603 | |||||||
| 48 | 150 | 104 | 66 | 48 | 1 | = | 417 |
| 24 | 374 | 180 | 252 | 96 | 119 | = | 1045 |
| 126 | 340 | 48 | 435 | 434 | 273 | = | 1656 |
| 600 | 92 | 506 | 315 | 180 | 665 | = | 2358 |
| 1080 | 377 | 756 | 297 | 494 | 125 | = | 3129 |
| 1188 | 350 | 476 | 198 | 512 | 992 | = | 3716 |
| = | = | = | = | = | = | ||
| 3066 | 1683 | 2070 | 1563 | 1764 | 2175 | 2271 |
As linhas, colunas e diagonais não apresentam Constante Mágica.
Soma total 12321.
| 1661 | |||||||
| 8 | 210 | 338 | 418 | 600 | 31 | = | 1605 |
| 4 | 272 | 252 | 560 | 312 | 544 | = | 1944 |
| 21 | 180 | 45 | 609 | 837 | 693 | = | 2385 |
| 100 | 40 | 368 | 330 | 252 | 1190 | = | 2280 |
| 180 | 143 | 459 | 253 | 551 | 175 | = | 1761 |
| 198 | 120 | 252 | 144 | 480 | 1152 | = | 2346 |
| = | = | = | = | = | = | ||
| 511 | 965 | 1714 | 2314 | 3032 | 3785 | 2358 |
As linhas, colunas e diagonais não apresentam Constante Mágica.
Soma total 12.321.
| 2603 | |||||||
| 248 | 750 | 494 | 286 | 168 | 1 | = | 1947 |
| 64 | 884 | 360 | 392 | 96 | 34 | = | 1830 |
| 231 | 540 | 63 | 435 | 279 | 63 | = | 1611 |
| 850 | 112 | 506 | 240 | 90 | 140 | = | 1938 |
| 1260 | 377 | 621 | 187 | 209 | 25 | = | 2679 |
| 1188 | 300 | 336 | 108 | 192 | 192 | = | 2316 |
| = | = | = | = | = | = | ||
| 3841 | 2963 | 2380 | 1648 | 1034 | 455 | 1836 |
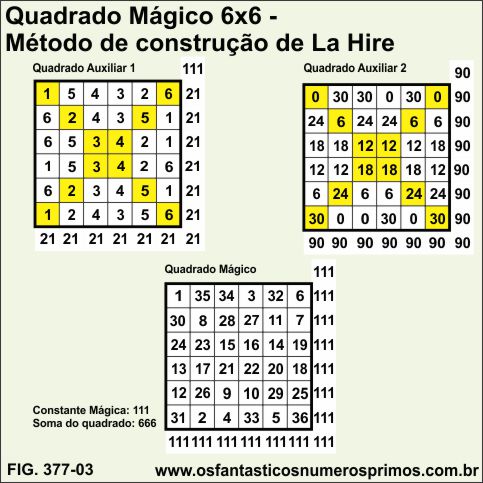
Na construção de quadrado mágico de ordem 6 utilizando o Método de La Hire, observa-se que os quadrados auxiliares 1 e 2 apresentam as seguintes Constantes Mágicas: 21 e 90.
As diagonais do quadrado auxiliar 1 são formadas por números naturais: {1, 2, 3, 4 5, 6} e do quadrado auxiliar 2 por múltiplos de 6: {0, 6, 12, 18, 24, 30}
Somando-se números de células correspondentes, obtem-se o Quadrado Mágico 6x6 de Constante Mágica 111 e Soma Total 666.
Para mais informações, veja matérias relacionadas abaixo.
Na decomposição do Quadrado Mágico 6x6 do Professor Vernon, nota-se que:
Nas linhas horizontais e diagonais números se repetem, o mesmo não acontece no Método de La Hire.
Não há Constante Mágica.
| 21 | |||||||
| 2 | 6 | 2 | 4 | 6 | 1 | = | 21 |
| 2 | 4 | 6 | 4 | 6 | 5 | = | 27 |
| 1 | 2 | 3 | 5 | 1 | 3 | = | 15 |
| 1 | 4 | 5 | 3 | 3 | 5 | = | 21 |
| 6 | 1 | 3 | 5 | 1 | 5 | = | 21 |
| 3 | 4 | 2 | 6 | 4 | 2 | = | 21 |
| = | = | = | = | = | = | = | |
| 15 | 21 | 21 | 27 | 21 | 21 | 15 |
Nas linhas verticais e na diagonal principal números se repetem, o mesmo não acontece no Método de La Hire.
Não há Constante Mágica.
| 90 | |||||||
| 6 | 24 | 24 | 18 | 18 | 0 | = | 90 |
| 0 | 30 | 12 | 24 | 6 | 12 | = | 84 |
| 6 | 18 | 0 | 24 | 30 | 18 | = | 96 |
| 24 | 0 | 18 | 12 | 6 | 30 | = | 90 |
| 30 | 12 | 24 | 6 | 18 | 0 | = | 90 |
| 30 | 6 | 12 | 0 | 12 | 30 | = | 90 |
| = | = | = | = | = | = | ||
| 96 | 90 | 90 | 84 | 90 | 90 | 54 |
Em 24 de agosto de 2.009, Francis Gaspalou, engenheiro frânces, idealizador do WebSite: https://www.gaspalou.fr
O método consiste em utilizar dois quadrados auxiliares irregulares em que números aparecem mais de uma vez em pelos menos em uma linha, coluna ou diagonais, semelhantes ao utilizados pelo Professor Vernon.
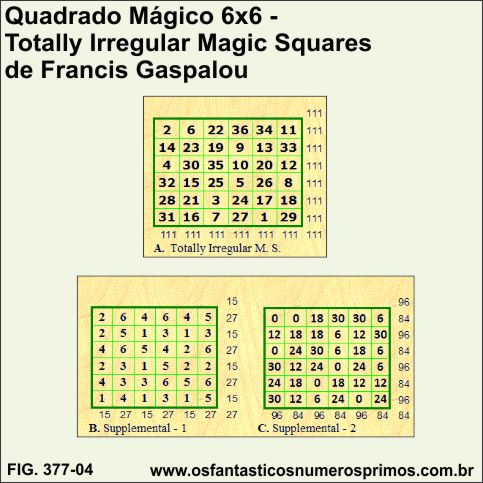
Interessante observar que foram realizadas as mesmas etapas acima com o Quadrado Mágico 6x6 Irregular de Francis Gasparou para se tentar reproduzir os resultados do Quadrado Mágico 6x6 e derivados do Professor Vernon, obtendo resultados parciais.
Autor: Ricardo Silva - abril / 2022
Jenkins, Vernon. WISDOM’S KEY: An examination of 666 as a number per se - www.whata
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://www.gaspalou.fr
www.magic

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato