


Imagine as seguintes situações:
Você têm 9 moedas, numeradas de 1 a 9. Qual é a chance de você jogá-las e elas cairem todas com as faces numeradas para cima?
Qual é a chance de você jogá-las e elas cairem com as faces numeradas para cima e ainda apresentar a configuração de um Quadrado Mágico?
Você têm 9 dados, numerados de 1 a 9 em uma só face, qual é a chance de jogá-los e eles cairem todos com as faces numeradas para cima?
Qual é a chance de você jogá-los e eles cairem com as faces numeradas para cima e ainda apresentar a configuração de um Quadrado Mágico?
Quadrado Mágico é um quadrado com células quadriculadas formadas por quantidades de números quadrados perfeitos, isto é, há quadrados mágicos formados por 9 células (3 x 3), 16 células (4 x 4), 25 células (5 x 5) e assim por diante...
Quadrado Mágico em que os números vão de 1 a n², formados por números distintos, dizemos que é um Quadrado Mágico Normal, Puro ou Elementar.
Os números são dispostos em certa ordem e a soma de cada linha, cada coluna, bem como cada diagonal tem como resultado um valor constante, o qual é chamada de Constante Mágica.
O aparecimento do Quadrado Mágico têm como origem a China, e se encontra documentado no Livro Os 9 capítulos da arte matemática no texto Shu Shu Shi Yu, baseado na estória do Imperador Yu que viu sair do Rio Lo (Rio Amarelo) uma tartaruga com marcas em formas de nós feitos em barbantes sobre seu casco.
O imperador Yu também observou que as marcas quando contadas nas horizontais, verticais e diagonais possuiam uma mesma soma, isto é, 15. A partir destes eventos a tartagura, que é um animal venerado pela sua longevidade na cultura chinesa, recebeu o nome de Lo-Shu e passou a ter carater místico e esotérico.
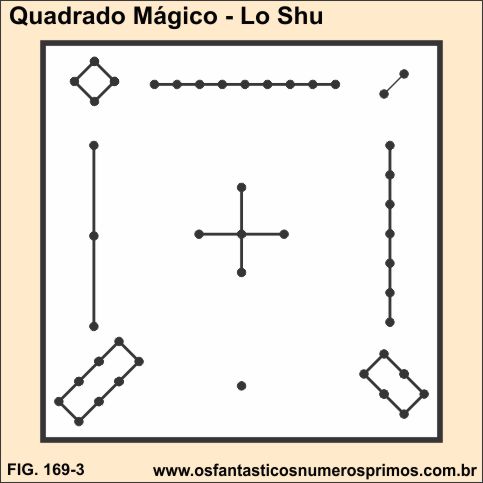
Quadrado Mágico Lo-Shu
Interessante observar no Lo-Shu, que as marcas com linhas e nós se transformaram em símbolos numéricos com as quais podem ser feitas contagens, utilizando operações matemáticas.
Um outro destaque importante é que cada símbolo numérico são formados por linhas e por pontos, dois dos três elementos primordiais da geometria.
E ainda vale destacar outros conceitos referentes aos tipos de números formados pelos símbolos no Lo-Shu:
a) números figurados quadrados: o 1 representado por ponto e o 4 representado por quadrado e pontos nos vértices;
b) números figurados retangulares: 6 e 8 representados por retângulos e respectivamente as suas quantidades em pontos;
c) números lineares: 2, 3, 5 e 7 (números primos) representados por linhas e respectivamente quantidades de pontos equidistantes.
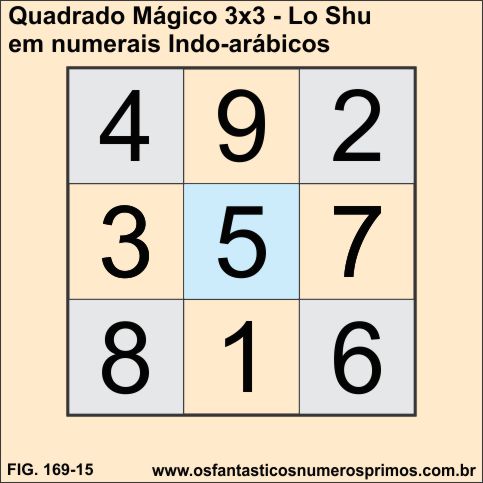
O Quadrado Mágico transcrito para o sistema de numeração indo-arábico nos permite também visualizar um "algo a mais" embutido na sua construção.
Podemos vê-lo como uma balança virtual, por exemplo, jamais poderíamos equilibrar 2 kilos de arroz com 8 quilos de arroz, mas no Quadrado Mágico há o constante equilíbrio exercído pelo número 5, ele é o eixo moderador de todos os números que o cercam.
As duplas de números com seus diferentes "pesos" formam o dobro do número central que os equilibram formando um conjunto harmonioso, pares com pares e ímpares com ímpares.
Os números são se repetem, se associam ao número central e formam uma quantidade constante que dá a magia ao quadrado.
"Prezado visitante, se você tiver o livro Os 9 capítulos da arte matemática - texto Shu Shu Shi Yu com a inscrição do Lo-Shu e puder enviá-la para ser divulgada nesta matéria, agradecemos de antemão"
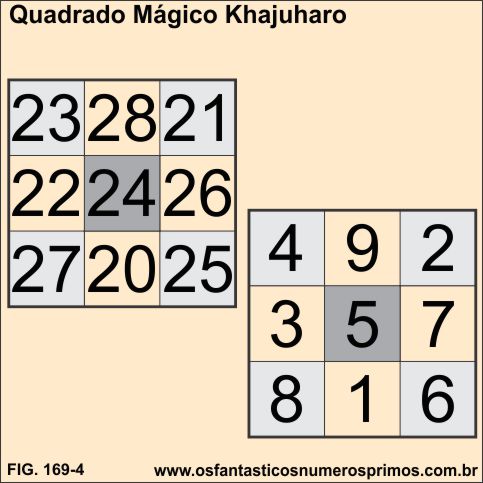
Na Índia, século XI, no piso em um dos templos da região de Khajuharo foi encontrado um Quadrado Mágico semelhante ao Lo-Shu.
No quadrado de Khajuharo foi adicionado 19 a cada número do Lo-Shu.
A Constante Mágica é 72.
A soma dos números é 216.
A disposição dos números apresentam algumas curiosidades, vejamos:
a) todos os números são de 20 a 28 - prevalece a vintena;
b) escreva o Lo-Shu de 21 a 29 e subtraia uma unidade, tem-se o o Quadrado Mágico Khajuharo;
c) nas células são acrescentadas nas casas das dezenas o 2 e nas casas das unidades o número têm uma unidade a menor do Lo-Shu.
d) não aparece o número 9;
e) aparece o número 20, aqui uma observação, como será que está a representação do Zero? Pois o símbolo do Zero apareceu por volta de 650 d.C.
"Prezado visitante, se você tiver imagem do piso do templo com a imagem do quadrado mágico e puder enviá-la para ser divulgada nesta matéria, agradecemos de antemão"
Acredita-se que o Templo Parshvanatha, região de Khajuraho na Índia, tenha sido construído por volta do ano 950 d.C, lá se encontra o Quadrado Mágico 4x4, também chamado de "Jaina Square" com a sequência numérica de 1 a 16.
É um dos quadrados mágicos perfeitos mais antigos de que se tem notícia e em sua configuração há as configurações pandiagonal e diabólico.
Quadrado Mágico Pandiagonal / Diabólico é quando as diagonais quebradas somam a Constante Mágica.
Constante Mágica: 34
Soma do números: 136

Fonte: https://commons.wikimedia.org/
wiki/File:Magic_square_at_the_Parshvanatha
_temple,_Khajuraho.png

Fonte: https://commons.wikimedia.org/wiki/
File:Le_temple_de_Parshvanath_(Khajuraho)_
(8638423582).jpg
Representação clássica de Quadrado Mágico na gravura "Melancolia" de Albrecht Durer.
Constante Mágica: 34
Soma do números: 136

Fonte: https://pt.wikipedia.org/
wiki/Quadrado_m%C3%A1gico
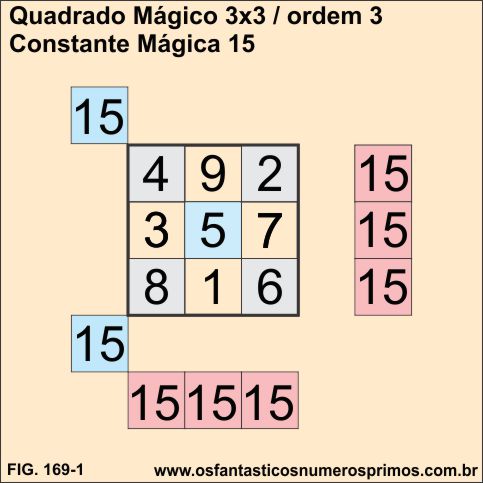
O Quadrado Mágico de ordem 3, assim é chamado porque é formado por 3 linhas e por 3 colunas, totalizando um total de 9 células (3²).
Os números de 1 a 9 são dispostos em certa ordem e a soma de cada linha, cada coluna e cada uma das diagonais tem como resultado 15, isto é, uma soma constante para ser denominado um Quadrado Mágico.
Esta soma comum das linhas, colunas e diagonais é chamada de Constante Mágica ou Soma Mágica.
Podem ser formados 362.880 combinações com o quadrado de ordem 3, mas somente 8 combinações formam Quadrados Mágicos.
| Quantidade de Combinações | |
|---|---|
| de Quadrados Mágicos | |
| Ordem | Quantidade |
| 3 (3x3) | 8 |
| 4 (4x4) | 880 |
| 5 (5x5) | 275.305.224 |
| 6 (6x6) | estima-se 1,7 x 10 19 |
Fonte: Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
| Quadrados Mágicos | ||
|---|---|---|
| e características numéricas | ||
| Quadrado Mágico | Constante Mágica | Soma Termos |
| 3 x 3 | 15 | 3 x 15 = 45 |
| 4 x 4 | 34 | 4 x 34 = 136 |
| 5 x 5 | 65 | 5 x 65 = 325 |
| 6 x 6 | 111 | 6 x 111 = 666 |
| 7 x 7 | 175 | 7 x 175 = 1225 |
| 8 x 8 | 260 | 8 x 260 = 2080 |
| 9 x 9 | 369 | 9 x 39 = 3321 |
Fonte: Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
Podemos determinar a Costante Mágica utilizando a seguintes fórmulas:
| 1 | ||||
| ___ | x | n | x | (n² + 1) |
| 2 |
Fonte: Carvalho, Maria Cecília Costa e Silva. Padrões Numéricos e Sequências - São Paulo: Moderna, 1977
Exemplo 1)
Quadrado de Ordem 3 e sua Constante Mágica
| 1 | ||||
| _______ | x | 3 | x | (3² + 1) |
| 2 |
| 1 | ||||
| _______ | x | 3 | x | (9 + 1) |
| 2 |
| 1 | ||||
| _______ | x | 3 | x | 10 |
| 2 |
| 1 | ||||
| _______ | x | 30 | ||
| 2 |
| 30 | ||||
| _______ | ||||
| 2 |
| 15 |
Ordem 3 x 15 (Constante Mágica) = 45 (Soma de todos dos termos de 1 a 9).
| (n + n3) |
| _______ |
| 2 |
Exemplo 2)
Quadrado de Ordem 3 e sua constante mágica.
| (n + n3) |
| _______ |
| 2 |
| (3 + 27) |
| _______ |
| 2 |
| (30) |
| _______ |
| 2 |
| 15 |
Ordem 3 x 15 (Constante Mágica) = 45 (Soma de todos dos termos de 1 a 9).
Podemos determinar a soma de todos os termos de uma Progressão Aritmética (PA) utilizando a seguintes fórmulas:
Soma de todos os termos (1, 2, 3, 4, 5, 6, 7, 8, 9) do Quadrado Mágico de ordem 3, onde:
a1 - primeiro termo
an - último termo
n - quantidade de termos
Sn - soma do termos
| (a1 + an) | ||||
| Sn | = | _____________ | x | n |
| 2 |
| (1 + 9) | ||||
| S9 | = | _____________ | x | 9 |
| 2 |
| 10 | ||||
| S9 | = | _____________ | x | 9 |
| 2 |
| S9 | = | 5 | x | 9 |
| S9 | = | 45 |
A soma de todos dos números 45 : 3 (ordem) = 15 (Constante Mágica).
A soma de todos números de um Quadrado Mágico Normal, Puro ou Fundamental pode ser obtido através da média aritmética do produto de um número quadrado perfeito com o seu sucessor.
Soma de todos os termos (1, 2, 3, 4, 5, 6, 7, 8, 9) do Quadrado Mágico de ordem 3
| n2 x ( n2 + 1 ) |
| _________ |
| 2 |
| 9 x ( 9 + 1 ) |
| _______ |
| 2 |
| 9 x ( 10 ) |
| _______ |
| 2 |
| 90 |
| ___ |
| 2 |
| 45 |
A soma de todos dos números 45 : 3 (ordem) = 15 (Constante Mágica).
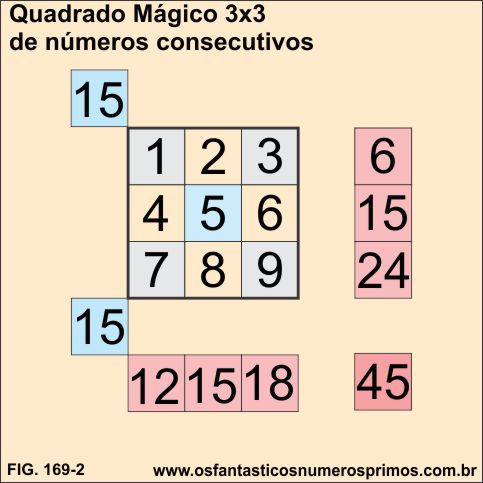
O presente exemplo de Números Consecutivos e o Quadrado se encontra publicado no livro Numeros Triangulares e Sequências Numéricas, onde foram feitos estudos das relações de números quadrados com números triangulares.
Diferentemente da ordem em que são dispostos os números em Quadrados Mágicos, os quadrados onde números são dispostos sequêncialmente, obtêm-se importantes relações, padrões e sequências numéricas, vejamos:
a) a soma de cada linha apresenta um múltiplo de 3, cujo um dos fatores estão na linha vertical central do quadrado.
2 x 3 = 6
5 x 3 = 15 (Constante Mágica)
8 x 3 = 24
b) a soma de cada coluna apresenta um múltiplo de 3, cujo um dos fatores estão na linha horizontal central do quadrado.
4 x 3 = 12
5 x 3 = 15 (Constante Mágica)
6 x 3 = 18
c) a soma de cada diagonal tem como resultado a Constante Mágica 15.
d) tanto a soma dos totais das linhas e das colunas tem como resultado 45, que é a soma de todos os números do quadrado.
e) o produto de 5 por 9 é igual a 45, o 5 se encontra no centro do quadrado e o 9 em um dos vértices.
f) o produto do quadrado de ordem 3 pela Constante Mágica tem como resultado a soma de todos os números do Quadrado Mágico.
3 x 15 = 45
Dispondo os números de 1 a 9 consecutivamente, conforme apresentado na tabela abaixo, podemos também obter outras informações que também ocorrem no Quadrado Mágico 3x3, bem como no estudo de Números Consecutivos e o Quadrado.
a) a soma dos termos equidistantes, que é 10, aparecem nos dois quadrados;
b) a soma dos termos equidistantes mais o termo central tem como resultado a Constante Mágica que é 15;
c) a soma dos termos equidistantes e o termo central tem como resultado o total de cada um dos quadrados que é 45;
d) 5 é o termo central tanto nos quadrados como na sequência de números consecutivos.
| Números Consecutivos | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Soma | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 9 | 10 | |||||||
| 2 | 8 | 10 | |||||||
| 3 | 7 | 10 | |||||||
| 4 | 6 | 10 | |||||||
| 5 | 5 | ||||||||
| 45 | |||||||||
O Quadrado Mágico é um excelente dispositivo numérico para se treinar o raciocínio lógico e matemático e também podendo ser utilizado como passatempo.
Há vários formatos de "dispositivos numéricos mágicos" que se valem do sistema do Quadrado Mágico Lo-Shu.
Encontrado nas ruínas de Pompéia é um exemplo clássico de quadrado mágico palíndrômico formado por palavras.
Pode ser lido da esquerda para a direita, da direita para esquerda, de baixo para cima, de cima para baixo e o significado de cada palavra continua sendo o mesmo.

Fonte:https://pt.wikipedia.org/
wiki/Pal%C3%ADndromo#/
media/File:Palindrom_TENET.svg
Excelente exemplo de construção de Quadrados Mágicos formados por 3 Quadrados Mágicos. A soma de todos os números do quadrado 3x3 e a soma de todos os números do quadrado 4x4 é igual a soma de todos os números do quadrado 5x5.
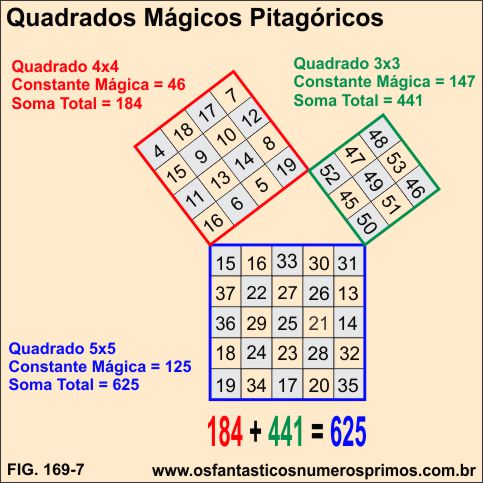
Fonte: Loomis, Elisha Scott. The Pythagorean Propositions - by The National Council of Teachers of Mathematics, Inc. - 1968
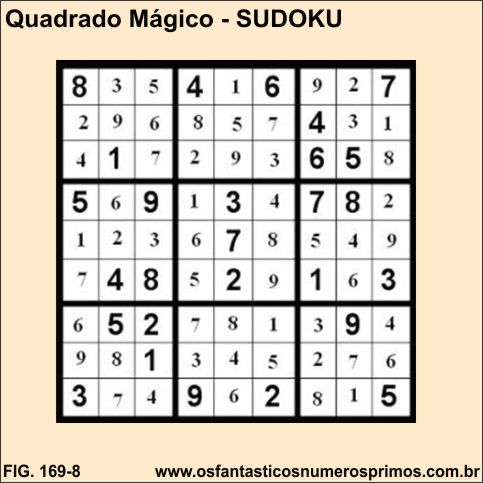
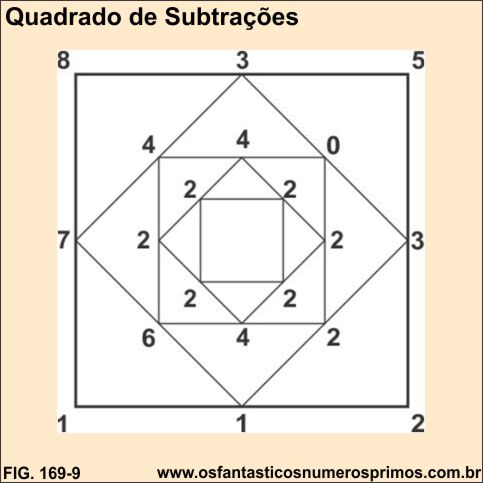
Veja matéria aqui no site:
011-estudos-115-quadrados-dinamicos
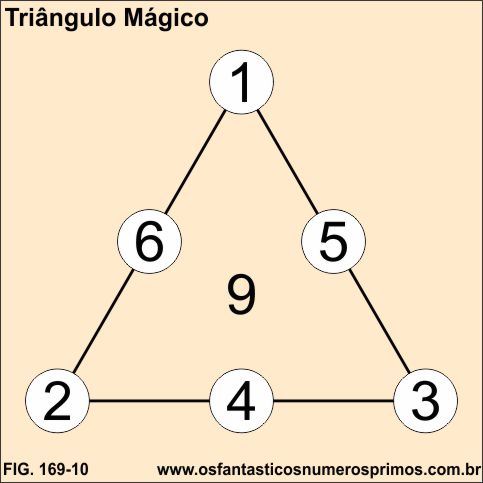
Fonte: Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017.96 p.
Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS,2017.
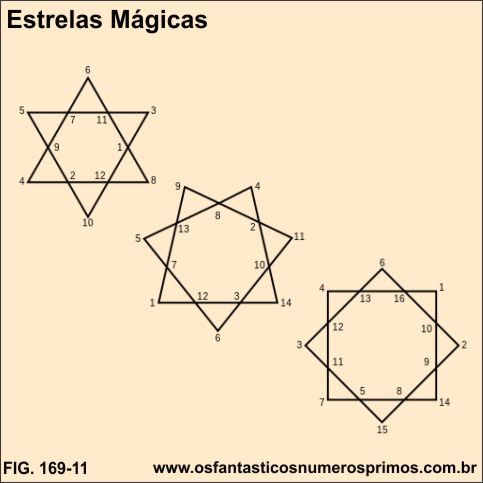
Fonte: https://pt.wikipedia.org/
wiki/Estrela_m%C3%A1gica
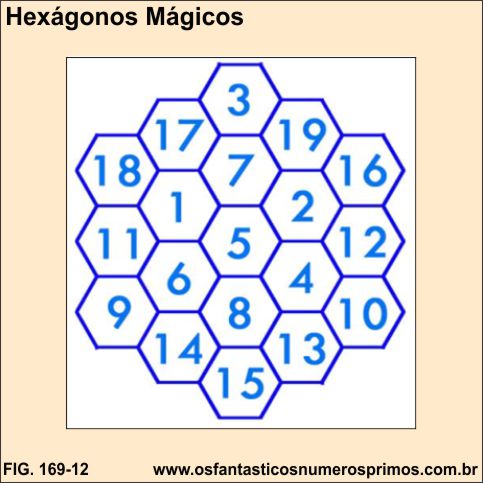
Fonte: Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensinofundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
maio/2018
https://commons.wikimedia.org/wiki
/File:Magic_square_at_the_Parshvanatha
_temple,_Khajuraho.png
https://commons.wikimedia.org/wiki
/File:Le_temple_de_Parshvanath_(Khajuraho)_
(8638423582).jpg
https://pt.wikipedia.org/wiki
/Quadrado_m%C3%A1gico
https://pt.wikipedia.org/wiki
/Pal%C3%ADndromo#/media/
File:Palindrom_TENET.svg
CARVALHO, Maria Cecília Costa e Silva. Padrões Numéricos e Sequências - São Paulo: Moderna, 1977
LOOMIS, Elisha Scott. The Pythagorean Propositions - by The National Council of Teachers of Mathematics, Inc. - 1968
MARQUES, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017.96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande –FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS,2017.
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato