capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Quadrados Mágicos 3x3 - 170

Quadrados Mágicos são dispositivos numéricos constituídos por quantidades iguais de linhas e colunas nos quais formando células podem ser dispostos sequências numéricas em certa ordem e que somadas tem como resultado um mesmo valor para cada linha, cada coluna e cada umas das diagonais.

Quadrados Mágicos conforme documentação histórica têm origem na China.

Os Quadrados Mágicos são classificados conforme a sua ordem:

Quadrado de Ordem 3 (3x3) é formado por 3 linhas e 3 colunas, totalizando um total de 9 células, o mesmo que 3² = 9.

Quadrado de Ordem 4 (4x4) é formado por 4 linhas e 4 colunas, totalizando um total de 16 células, o mesmo que 4² = 16.

Quadrado de Ordem 5 (5x5) é formado por 5 linhas e 5 colunas, totalizando um total de 25 células, o mesmo que 5² = 25 e assim sucessivamente.

Quadrados mágicos e progressão aritmética

A seguinte sequência numérica é denominada de Progressão Aritmética Finita com as seguintes características:

a) possui 9 termos, sendo seu primeiro terno iniciando-se em 1 e terminando em 9;

b) a diferença entre cada um dos seus termos, isto é, a sua razão é de uma unidade;

c) a soma de dois termos equidistantes tem o mesmo valor, que é 10;

d) o quociente da soma de dois termos equidistantes tem o mesmo valor, que é 5 e também o seu termo central;

e) a soma de todos os termos é 45;

f) 45 é multiplo de 3, de 5 e de 9.

Progressão Aritmética

									Soma
1	2	3	4	5	6	7	8	9

1								9	10
	2						8		10
		3				7			10
			4		6				10
				5					5
									45

Quadrados cujas sequências númericas são formadas por 9 termos é denominado de Quadrado Mágico 3x3 ou de ordem 3.

O Quadrado Mágico 3x3, cujos termos são de 1 a 9 tem certa primazia entre os demais quadrados mágicos, vejamos:

a) foi o primeiro tipo de quadrado mágico construído com notação numérica, dando a ideia de sequência e quantidade;

b) é um quadrado que apresenta a sequência dos primeiros números inteiros de 1 a 9;

c) a partir dele, houveram grandes estudos matemáticos e também se criaram outros tipos de quadrados mágicos e dispositivos mágicos como triângulos, hexágonos, estrelas, cubos, etc.

Construindo Quadrados Mágicos 3x3

Transportando-se a progressão aritmética de 1 a 9 para um quadrado de 3 linhas por 3 colunas, constrói-se um Quadrado Mágico 3x3 com as seguintes propriedades:

a) o termo central do quadrado é o número 5, o mesmo da progressão aritmética;

b) os termos dos vértices são números pares;

c) os ternos centrais das laterais são números ímpares;

d) a soma de cada linha horizontal e vertical é 15;

e) a soma de cada diagonal é 15;

d) a Constante Mágica é 15;

e) a soma de dois números equidistante dos extremos é 10 e a sua metade é o termo central 5;

f) o produto de 3 (ordem) por 5 (termo central) tem como resultado a Constante Mágica 15;

g) a soma dos números pares dos vértices é 20, o quádruplo de 5;

h) a soma dos números ímpares centrais das laterais é 20, o quádruplo de 5.

Observação: a diagonal principal (da esquerda superior para a direita inferior) ou a diagonal secundária os números 4, 5 e 6 aparecem em ordem crescente ou decrescente em suas oito combinações a partir da configuração do Quadrado Mágico Lo-Shu.

Nos Quadrados Mágicos de ordem 3 cujo termo central é um número ímpar, os números da coluna e linha centrais são formados por números ímpares.

quadrado mágico 3x3 - constante mágica 15

Quadrados Mágicos 3x3 e métodos de construções

Método da adição e subtração

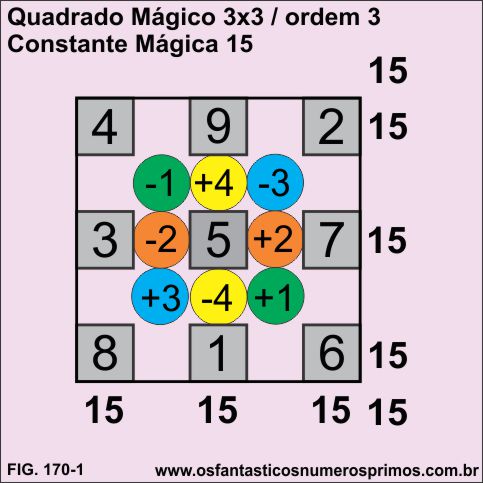
Este método de construção de quadrado mágico consiste em somar e subtrair valores a partir do termo central.

1) coloque o termo central no centro do quadrado, o número 5

2) 5 - 4 = 1

coloque o 1 na lateral central inferior do quadrado

3) 5 + 4 = 9

coloque o 9 na lateral central supeior do quadrado

4) 5 - 2 = 3

coloque o 3 na lateral central esquerda do quadrado

5) 5 + 2 = 7

coloque o 7 na lateral central direita do quadrado

6) 5 - 3 = 2

coloque o 2 no canto superior direito do quadrado

7) 5 + 3 = 8

coloque o 8 no canto inferior esquerdo do quadrado

8) 5 -1 = 4

coloque o 4 no canto superior esquerdo do quadrado

9) 5 + 1 = 6

coloque o 6 no canto superior direito do quadrado

Método da "cruz" e "xis"

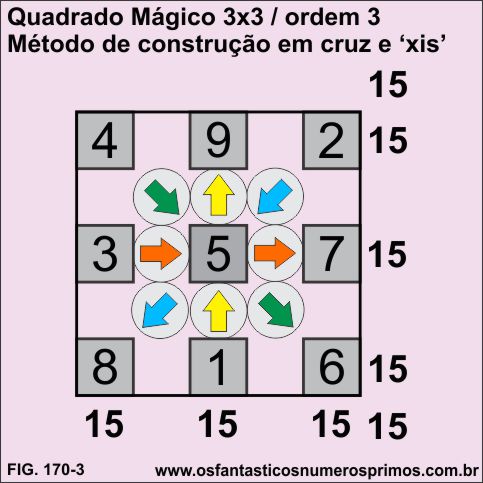
Consiste em construir um quadrado mágico de ordem 3 fazendo movimentos de uma cruz e da letra "xis" de forma que se parta sempre de um número menor para um número maior.

Progressão Aritmética

									Soma
1	2	3	4	5	6	7	8	9

1								9	10
	2						8		10
		3				7			10
			4		6				10
				5					5
									45

a) a partir do centro da base do quadrado marque o 1 e depois marque o 9 no topo (setas amarela), dessa forma você "desenhou" o mastro da cruz.

b) da lateral esquerda central para a direita marque o 3 e depois o 7 (setas laranja), dessa forma você "desenhou" o trave da cruz.

c) em diagonal, do canto direito superior para o inferior marque o 2 e depois o 8 (setas azul).

d) em diagonal, do canto esquerdo superior para o inferior marque o 4 e depois o 6 (setas verde).

quadrado mágico 3x3 - construção em cruz e xis

Método da rotação

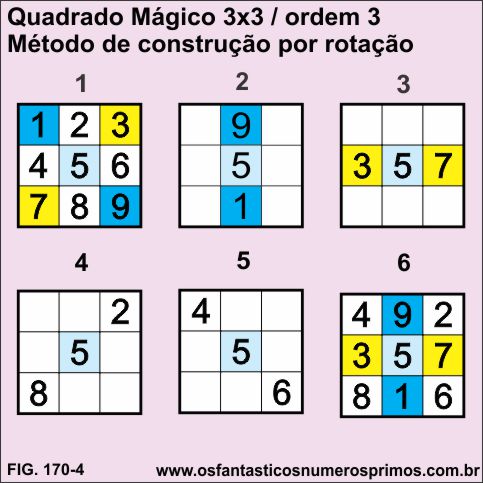
Este método consiste em colocar primeiramente os termos em sequência dentro do quadrado 3x3, posteriormente desenha-se um novo quadrado quadriculado e finalmente rotaciona dois termos equidistantes para formar o Quadrado Mágico.

1) monte o quadrado conforme o modelo;

2) em um novo quadrado gire em sentido anti-horário a dupla de números ímpares 1 e 9 de forma que dois fiquem em sentido vertical;

3) gire em sentido anti-horário a dupla de números ímpares 3 e 7 de forma que os dois fiquem em sentido horizontal;

4) gire em sentido horário a dupla de números pares 2 e 8 de forma que os dois fiquem em sentido diagonal (diagonal secundária);

5) gire em sentido horário a dupla de números pares 4 e 6 de forma que os dois fiquem em sentido diagonal (diagonal principal).

Através deste método, as duplas de números ímpares que estavam em sentidos diagonais passam uma para a vertical e a outra para a horizontal e de forma inversa as duplas de números pares.

Quadrado Mágicos 3x3 - Método de construção por rotação

Método de construção Simom De La Loubère (Método Siamês)

Simom de La Loubère, diplomata francês, em missão para o governo de Luiz XIV em Sião (hoje Tailândia), escreveu Du Royaume de Siam em 1693, onde descreve um método de construção para quadrados mágicos de ordem ímpar.

Este método consiste em construir um quadrado mágico com números sucessivos deslocando-os diagonalmente para cima e para direita.

quadrado mágico 3x3 - método de construção De La Loubere (Siamês)

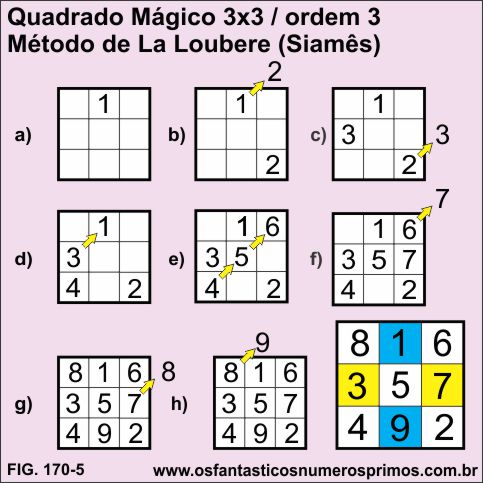
a) colocar o número 1 na casa central superior;

b) o número 2 (fica fora do quadrado), então deve ser colocado na última casa da coluna 3;

c) o número 3 (fica fora do quadrado), então deve ser colocado na primeira casa da linha central;

d) o número 4 não pode ficar na casa do número 1, então ele dever ser colocado abaixo do 3;

Observação: o número 4 está sendo colocado abaixo de um múltiplo de 3 e que 3 é a ordem do quadrado mágico.

e) os números 5 e 6 são colocados sequencialmente pois as casas estão vazias;

f) o número 7 fica fora do quadrado (não há colunas e linhas para ele ser colocado ou como se tivesse uma casa ocupada), então ele deve ser colocado abaixo do número 6;

Observação: o número 7 está sendo colocado abaixo de 6 que é múltiplo de 3 e que também é a ordem do quadrado mágico.

g) o número 8 (fica fora do quadrado), deve ser colocado na primeira casa da primeira linha;

h) o número 9 (fica fora do quadrado), deve ser colocado na última casa da coluna do meio.

Comparando com a configuração do quadrado Lo-Shu, nesta construção, a linha 1 passou a ser a linha 3 e a linha 3 passou a ser a linha 1.

Quadrado Mágico 3x3 e números quadrados perfeitos

Elevando-se os números de 1 a 9 do Quadrado Mágico 3x3 ao quadrado, obtem-se um Quadrado Mágico Imperfeito com as seguintes características:

Quadrado Mágico
Lo-Shu 3x3 ao quadrado
			93

16	81	4	101
9	25	49	83
64	1	36	101

89	107	89	77

a) a soma dos números quadrados perfeitos (89) da primeira linha é igual a soma dos quadrados da terceira linha;

Observação: 89 é um número primo.

b) a soma dos números quadrados perfeitos da primeira coluna é igual a soma dos quadrados da terceira coluna;

c) a soma da linha central 83 é um número primo;

d) a soma da coluna central 107 é um número primo;

e) a soma da diagonal principal 77 é múltiplo de 7;

f) a soma da diagonal secundária é múltiplo de 3.

Can a 3x3 magic square be constructed with nine distinct square numbers? This short question asked by Martin LaBar in 1984 became famous when Martin Gardner republished it in 1996 and offered $100 to the first person to construct such a square. Two years later, Gardner wrote:

So far no one has come forward with a “square of squares” – but no one has proved its impossibility either. If it exists, its numbers would be huge, perhaps beyond the reach of today’s fastest computers.

Fonte: http://www.multimagie.com

Pode um quadrado mágico de 3x3 ser construído com nove números quadrados distintos? Esta pequena pergunta feita por Martin LaBar em 1984 tornou-se famosa quando Martin Gardner a republicou em 1996 e ofereceu US$ 100 para a primeira pessoa a construir tal quadrado. Dois anos depois, Gardner escreveu:

Até agora ninguém avançou com um “quadrado de quadrados” - mas ninguém provou sua impossibilidade. Se existir, seus números seriam enormes, talvez além do alcance dos computadores mais rápidos de hoje.

Quadrado Mágico 3x3 e números cúbicos

Elevando-se os números de 1 a 9 do Quadrado Mágico 3x3 ao cubo, obtem-se um Quadrado Mágico Imperfeito com as seguintes características:

a) as diagonais não formam Costantes Mágicas;

b) as linhas não formam Costantes Mágicas;

c) as colunas não formam Costantes Mágicas.

Quadrado Mágico
Lo-Shu 3x3 ao cubo
			645

64	729	8	801
27	125	343	495
512	1	216	729

603	855	567	405

Quadrado Mágico de Constante Mágica par

Pode-se construir infinitos Quadrados Mágicos de ordem 3.

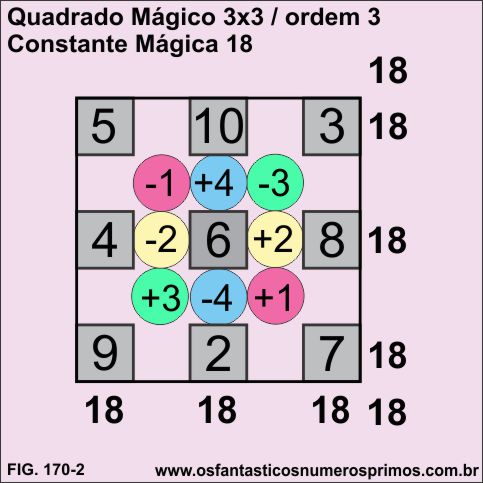
Multiplicando a ordem 3 por um número acima de 5, neste exemplo, o número 6 obtem-se a Constante Mágica 18.

Para melhor visualizar a sequência dos números, a partir da tabela da progressão aritmética finita de 9 termos, começando pelo número par 2.

Progressão Aritmética

									Soma
2	3	4	5	6	7	8	9	10

2								10	12
	3						9		12
		4				8			12
			5		7				12
				6					6
									54

Seguindo-se os métodos de construções de Quadrado Mágico de ordem 3 apresentadas acima, obtemos o seguinte Quadrado Mágico de Constante Mágica 18.

Observação: a diagonal principal (da esquerda superior a direita inferior) ou a diagonal secundária os números 5, 6 e 7 aparecem em ordem crescente ou decrescente em suas oito combinações a partir da configuração do Quadrado Mágico Lo-Shu.

Nos Quadrados Mágicos 3x3 cujo termo central é um número par, os números da coluna e linha centrais são formados por números pares.

quadrado mágico de 3x3 - constante mágica 18

Desafio ao visitante

O Web-Site Os Fantásticos Números Primos lança um desafio a você estimado visitante: de construir um triângulo pitagórico inscrito numa circunferência somente com régua não graduada e compasso semelhante ao triângulo retângulo de 30, 60 e 90 graus para ser publicado na Seção Texto do WebSite.

Enviando o seu estudo e modelo matemático da sua solução, para o nosso e:mail:

contato@osfantasticosnumerosprimos.com.br,

você receberá como cortesia:

O livro digital OS FANTÁSTICOS NÚMEROS PRIMOS

Veja as matérias:

005-texto-017-triangulos-pitagoricos-inscrito-semicircunferencia

005-texto-018-triangulo-pitagorico3-4-5-inscrito-semicircunferencia

sobre construções de triângulos.

Autor: Ricardo Silva - maio/2018