


Um outro método para se obterem números quadrados perfeitos é partir da Fórmula de Euclides, fórmula esta utilizada para se gerarem ternos pitagóricos.
Ternos pitagóricos é uma sequência de três números inteiros que satisfazem ao Teorema de Pitágoras "O quadrado da hipotenusa é igual a soma dos quadrados dos quatetos" - (a² = b² + c²), de forma que a soma de dois números inteiros elevados ao quadrado tenha como resultado um outro número quadrado perfeito.
As Fórmulas de Euclides parte do seguinte princípio: escolhendo-se dois números primos entre si, podem ser gerados ternos pitagóricos primitivos.
Números primos entre sim são números que tem como divisor comum o número 1.
Na prática, dois números consecutivos são números primos entre si.
Exemplos:
2 e 3;
3 e 4;
4 e 5, etc.
Ternos pitagóricos primitivos são os que podem gerar outros tipos ternos pitagóricos que são chamados de ternos pitagóricos derivados.
Escolhendo-se tanto números primos entre si quanto números não primos entre si, podemos gerar uma infinidade de ternos pitagóricos primitivos e derivados sequencialmente.
A partir de dois números naturais m>n e os substituindo nas Fórmula de Euclides a seguir, encontramos o termos a, b e c do Teorema de Pitágoras e consequentemente o Terno Pitagórico.
a = m² - n²
b = 2mn
c = m² + n²
onde:
m > n (m tem que ser maior que n)
m e n tem que ser primos entre si
A tabela apresenta os primeiros 14 ternos pitagóricos primitivos (a-b-c) gerados de sequências de números primos entre si.
Na coluna (a) foram gerados a sequência de números ímpares: 3, 5, 7, 9, 11,... e que são as raízes quadradas da soma do termos (b) e (c).
Nas colunas (b) e (c) foram gerados sequências de números consecutivos: (4,5), (12,13), (24,25),...
Na coluna (b) os números são pares e na coluna (c) ímpares.
| Tabela de | ||||||
|---|---|---|---|---|---|---|
| ternos pitagóricos primitivos | ||||||
| coluna | coluna | coluna | ||||
| Termos | ||||||
| m | n | m² | n² | a | b | c |
| 2 | 1 | 4 | 1 | 3 | 4 | 5 |
| 3 | 2 | 9 | 4 | 5 | 12 | 13 |
| 4 | 3 | 16 | 9 | 7 | 24 | 25 |
| 5 | 4 | 25 | 16 | 9 | 40 | 41 |
| 6 | 5 | 36 | 25 | 11 | 60 | 61 |
| 7 | 6 | 49 | 36 | 13 | 84 | 85 |
| 8 | 7 | 64 | 49 | 15 | 112 | 113 |
| 9 | 8 | 81 | 64 | 17 | 144 | 145 |
| 10 | 9 | 100 | 81 | 19 | 180 | 181 |
| 11 | 10 | 121 | 100 | 21 | 220 | 221 |
| 12 | 11 | 144 | 121 | 23 | 264 | 265 |
| 13 | 12 | 169 | 144 | 25 | 312 | 313 |
| 14 | 13 | 196 | 169 | 27 | 364 | 365 |
| 15 | 14 | 225 | 196 | 29 | 420 | 421 |
| www.osfantasticosnumerosprimos.com.br | ||||||
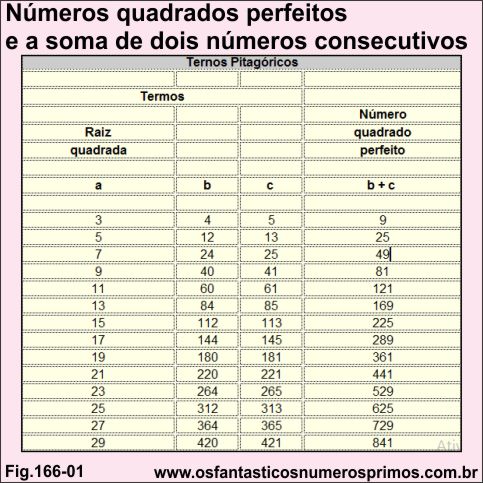
Uma importante propriedade que se pode extrair dos ternos pitagóricos primitivos é que a soma dos termos (b) e (c) tem como resultado um número quadrado perfeito ímpar gerado pela soma de dois números consecutivos.
Aqui uma ressalva, conforme estudos publicados no livro Ternos Pitagóricos e Sequências Numéricas, só Ternos Primitivos Pitagóricos de Ordem Triangular possuem estas características, pois Ternos Pitagóricos Primitivos de Ordem Não Triangular, Ternos Pitagóricos Primitivos Raros e Ternos Derivados não os possuem.
| Ternos Pitagóricos | |||
|---|---|---|---|
| Termos | |||
| Número | |||
| Raiz | quadrado | ||
| quadrada | perfeito | ||
| a | b | c | b + c |
| 3 | 4 | 5 | 9 |
| 5 | 12 | 13 | 25 |
| 7 | 24 | 25 | 49 |
| 9 | 40 | 41 | 81 |
| 11 | 60 | 61 | 121 |
| 13 | 84 | 85 | 169 |
| 15 | 112 | 113 | 225 |
| 17 | 144 | 145 | 289 |
| 19 | 180 | 181 | 361 |
| 21 | 220 | 221 | 441 |
| 23 | 264 | 265 | 529 |
| 25 | 312 | 313 | 625 |
| 27 | 364 | 365 | 729 |
| 29 | 420 | 421 | 841 |
| www.osfantasticosnumerosprimos.com.br | |||
Veja que números quadrados perfeitos pares não podem ser obtidos pela soma de dois números consecutivos.
Exemplos:
a) Quadrado 4
2 + 2 = 4
2 + 3 = 5
b) Quadrado 16
8 + 8 = 16
8 + 9 = 17
c) Quadrado 36
18 + 18 = 36
18 + 19 = 37
Autor: Ricardo Silva - maio/2018
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato