


Terno Pitagórico, Tripla Pitagórica ou simplesmente Trinca Pitagórica é um conjunto de três números inteiros que satisfazem ao Teorema de Pitágoras (a² = b² + c²) - "O quadrado da hipotenusa é ígual a soma dos quadrados dos quatetos".
Elevando-se dois números inteiros ao quadrado e depois somando-os e extraindo a raiz quadrada da soma e está raiz sendo um número inteiro, então os números formam Terno Pitagórico.
Um estudo sistemático publicado no livro Ternos Pitagóricos e Sequências Numéricas demonstram interessantes propriedades, regularidades e padrões numéricos com as sequências dos termos pitagóricos utilizando-se as Fórmulas de Euclides.
Duas das principais descobertas relatadas no livro são as relações dos números triangulares com a sequência dos ternos pitagóricos e os números multiplos de 4.
Destas relações foram possíveis elaborar dois algoritmos distintos para se gerarem ternos pitagóricos a partir de um número múltiplo de 4.
Foram gerados cerca de 1.000 ternos pitagóricos, e num primeiro momento, para melhor estudá-los, eles foram classificados conforme o tipo de regularidade que cada grupo apresentava, e assim, foram categorizados:
a) Ternos Pitagóricos Primitivos de Ordem Triangular;
b) Ternos Pitagóricos Primitivos de Ordem Não Triangular;
c) Ternos Pitagóricos Derivados Pares;
d) Ternos Pitagóricos Derivados Ímpares;
e) Ternos Pitagóricos Raros.
Utilizando as Fórmulas de Euclides com números primos entre si e números não primos entre si, podem ser gerados sequencialmente ternos pitagóricos primitivos e derivados.
Escolhendo-se dois números naturais m>n e os substituindo nas Fórmulas de Euclides a seguir, encontramos o termos a, b e c do Teorema de Pitágoras e consequentemente o Terno Pitagórico.
a = m² - n²
b = 2mn
c = m² + n²
onde:
m > n (m tem que ser maior que n).
m e n tem que ser primos entre si.
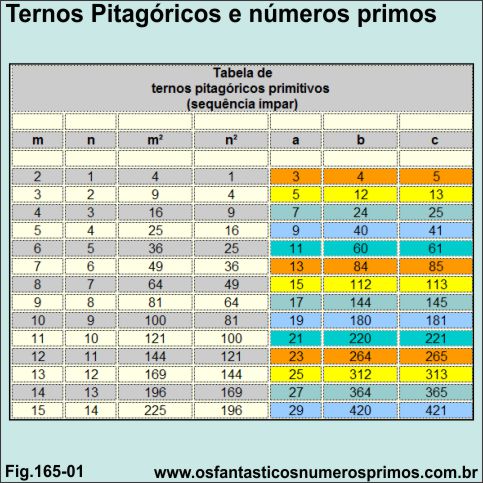
A presente tabela foi gerada a partir de números primos entre si onde tem-se os primeiros 14 ternos pitagóricos de ordem triangular, onde se constatam as seguintes regularidades:
a) sendo uma unidade de diferença entre os números entre si, a coluna (a) têm como resultados a sequência de números ímpares: 3, 5, 7, 9, 11,... e entre eles, ocorrências de números primos: 3, 5, 7, 11, 13, 17,...;
b) o segundo termo de um Terno Primitivo de Ordem Triangular é um número par;
c) os ternos pitagóricos (3, 4 e 5) e (5, 12 e 13) são os únicos ternos com a ocorrência do número primo 5;
d) nos ternos pitagóricos cujos primeiros termos terminam em 3, excetuando-se o terno 3, 4 e 5, só no primeiro termo poderá ocorrer número primo;
e) nos ternos cujos primeiros termos terminam em 5, só o terceiro termo poderá ocorrer número primo;
f) nos ternos cujos primeiros termos terminam em 7, só o primeiro termo poderá ocorrer número primo;
g) nos ternos cujos primeiros termos terminas em 9, só o primeiro e terceiro termos poderão ocorrer números primos;
i) nos ternos cujos primeiros termos terminam em 1, só o primeiro e terceiro termos poderão ocorrer números primos.
| Tabela de ternos pitagóricos primitivos (sequência ímpar) |
||||||
|---|---|---|---|---|---|---|
| m | n | m² | n² | a | b | c |
| 2 | 1 | 4 | 1 | 3 | 4 | 5 |
| 3 | 2 | 9 | 4 | 5 | 12 | 13 |
| 4 | 3 | 16 | 9 | 7 | 24 | 25 |
| 5 | 4 | 25 | 16 | 9 | 40 | 41 |
| 6 | 5 | 36 | 25 | 11 | 60 | 61 |
| 7 | 6 | 49 | 36 | 13 | 84 | 85 |
| 8 | 7 | 64 | 49 | 15 | 112 | 113 |
| 9 | 8 | 81 | 64 | 17 | 144 | 145 |
| 10 | 9 | 100 | 81 | 19 | 180 | 181 |
| 11 | 10 | 121 | 100 | 21 | 220 | 221 |
| 12 | 11 | 144 | 121 | 23 | 264 | 265 |
| 13 | 12 | 169 | 144 | 25 | 312 | 313 |
| 14 | 13 | 196 | 169 | 27 | 364 | 365 |
| 15 | 14 | 225 | 196 | 29 | 420 | 421 |
Autor: Ricardo Silva - maio/2018
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato