capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Quadrados Mágicos 6x6 - 193

Quadrado Mágico 6x6 ou de ordem 6 é um quadrado quadriculado formado por 6 linhas e 6 colunas perfazendo um total de 36 células.

O Quadrado Mágico 6x6 Normal ou Puro tem como formação a progressão aritmética finita constituída pelos 36 primeiros números naturais (1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11, 12 , 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35 e 36) ou 1 a n², tendo como Constante Mágica 111 e soma do quadrado 666.

Quadrado Mágico 6x6 e o Método de Construção Fhilipe de la Hire

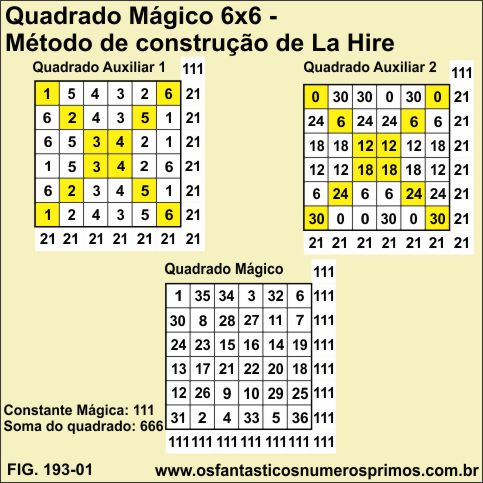
Fhilipe de la Hire (1640-1718) encontrou o Tratado de Matemática sobre Quadrados Mágicos de Manuel Moschopoulos (1265 d.C ?) na Biblioteca Real de Paris no final do Séc. XVII [1]

Quadrados Mágicos de ordem par que não são múltiplos de 4 têm métodos específicos de construções, O Métódo de Fhilipe de la Hire [1] é um deles e funciona a partir de dois quadrados auxiliares para se construir Quadrado Mágico de ordem 6.

a) monta-se o quadrado auxiliar 1 com a sequência dos números naturais de 1 a 6 nas diagonais;

b) preenchem-se as colunas, repetindo os números conforme o exemplo;

c) monta-se o quadrado auxliar 2 com a sequência dos múltiplos de 6 de 0 a 30 na diagonais;

d) preenchem-se as linhas, repetido os números conforme o exemplo;

e) por fim, somam-se os números de cada uma das células de mesmas posições obtendo-se assim um Quadrado Mágico 6x6.

quadrado mágico 6x6 - método de construção De La Hire

Quadrado Mágico de 6x6 e o Método de Construção Simon de la Loubère

Simon de la Loubère (1642-1729) escreveu Royaume de Siam (Métodos de Construção de Quadrados Mágicos) em 1691, ele fez parte de uma Missão Diplomática enviada pelo governo francês.

O Método de Construção de Quadrado Mágico de Simon de la Loubère [2] para quadrados mágicos de ordem par não múltiplos de 4 constiste em dividir em 4 áreas um Quadrado Mágico de ordem 6 (áreas A, B, C e D), o mesmo montar quatro Quadrados Mágicos de ordem 3 compondo um Quadrado Mágico de ordem 6.

a) constrói-se um Quadrado Mágico de ordem 3 (área A - cor azul), podendo ser utilizados os métodos de construções: " Cruz e Xis", Rotação, Adição e Subtração, Pirâmide, etc. (veja máterias aqui no site);

b) constrói-se o segundo Quadrado Mágico de ordem 3 (área B - cor verde) , somando-se 9 a cada elemento do quadrado A;

c) constrói-se o terceiro Quadrado Mágico de ordem 3 (área C - cor rosa), somando-se 18 a cada elemento do quadrado A;

d) constrói-se o quarto Quadrado Mágico de ordem 3 (área D - cor lilás), somando-se 27 a cada elemento do quadrado A;

quadrado mágico 6x6 - método de construção LOUBERE

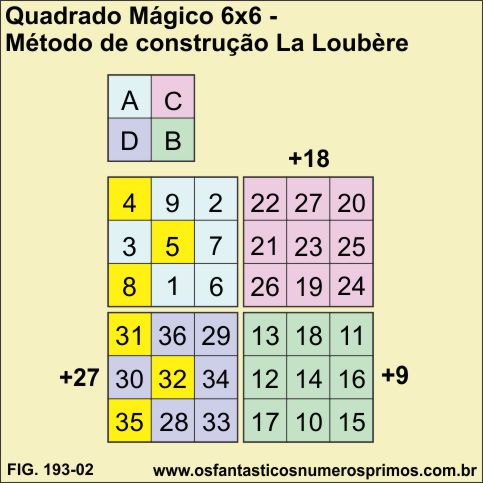
e) os números 4, 5 e 8 devem ser deslocados para o quadrado de baixo;

f) os números 31, 32 e 35 devem ser deslocados para o quadrado de cima.

Observação: juntando-se sequecialmente os números dos sub-quadrados, eles formam a progressão aritmética de 1 a 36.

Quadrado Mágico 6x6 e o Método de Construção LUX

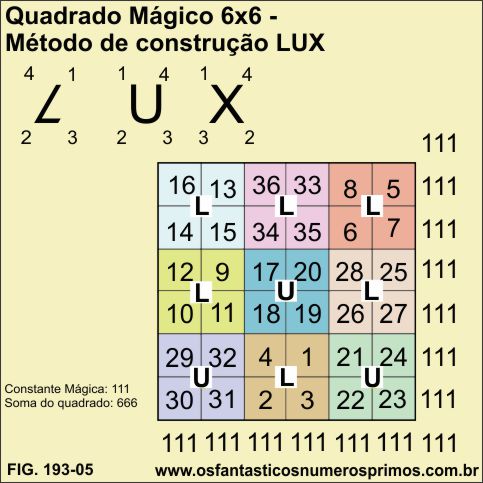
O Método LUX de construção de Quadrados Mágicos de ordem par não múltiplos de 4 foi desenvolvido pelo matemático britânico John Horton Conway.

O Método LUX consiste em dividir uma matrix de 6 x 6 (36 quadrados) em 9 áreas quadradas de 2 x 2.

As áreas quadradas de 2 x 2 formam um Quadrado Mágico de ordem 3 e serve como base para a montagem (números na cor cinza) do quadrado de ordem 6.

Colocam-se as letras "L" e "U" no centro de cada área quadrada de 2x2.

Seguindo o esquema das letras "L" e "U" de distribruição e ordem de números, começa-se a inserir a sequência dos números de 1 a 36 de 4 em 4 números, iniciando-se na área onde está o número 1 (cor cinza).

Onde está o número 1 (cor cinza), inserem-se 1, 2, 3 e 4 seguindo o esquema de distribuição de números da letra "L".

Onde está o número 2 (cor zinza), inserem-se 5, 6, 7 e 8 seguindo o esquema de distribuição de números da letra "L".

quadrado mágico 6x6 - método de construção lux

Seguindo a ordem dos números na cor cinza e as letras "L" e "U" e inserindo números de 4 em 4, finaliza-se o Quadrado Mágico de ordem 6.

Quadrado Mágico 6x6 soma mágica 111

Quadrado Mágico 6x6 soma mágica 111 possui as seguintes propriedades numéricas:

a) Constante Mágica e soma do quadrado;

Constante Mágica: 111

Soma do quadrado: 666

Quadrado Mágico 6x6
constante mágica 111
						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

b) cada área amarela tem a soma de 126;

c) cada área laranja tem a soma de 207;

d) 126 + 207 = 333 (metáde da soma do quadrado 666)

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

e) a soma dos números do vértices, formando cantoneiras tem com resultado 222 ( um terço da soma do quadrado 666);

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

f) a soma dos números formando um "octógono" tem com resultado 222 (um terço da soma do quadrado 666);

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

g) a soma dos números formando uma "cuz" tem com resultado 222 (um terço da soma do quadrado 666).

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

O quadrado mágico 6x6 e números quadrados perfeitos

Elevando-se os números de 1 a 36 do Quadrado Mágico de ordem 6 ao quadrado, obtem-se um Quadrado Mágico Imperfeito com as seguintes características:

a) as colunas 1 e 3 apresentam o mesmo resultado 3175;

b) as colunas 4 e 6 apresentam o mesmo resultado 2203;

c) as linhas 2 e 5 apresentam o mesmo resultado 2677.

Quadrado Mágico 6x6
números quadrados perfeitos
						2535

961	81	4	484	729	400	2659
9	1024	49	441	529	625	2677
1225	1	36	676	361	576	2875
16	1296	841	169	324	121	2767
900	25	1156	144	196	256	2677
64	784	1089	289	100	225	2551

3175	3211	3175	2203	2239	2203	2611

O Quadrado Mágico 6x6 e números consecutivos

No livro Sequências Numéricas Magicas [3] estão publicados vários estudos sobre relações numéricas entre figuras geométricas, números figurados, naturais, quadrados, cúbicos, etc.

Em um desses estudos, os 36 primeiros números naturais são dispostos sequencialmente dentro de um quadrado 6x6 apresentando entre outras, as seguintes propriedades numéricas:

Quadrado Mágico 6x6
números consecutivos
						111

1	2	3	4	5	6	21
7	8	9	10	11	12	57
13	14	15	16	17	18	93
19	20	21	22	23	24	129
25	26	27	28	29	30	165
31	32	33	34	35	36	201

96	102	108	114	120	126	111

a) as diagonais tem como resultado a Constante Mágica 111;

b) a soma de cada da linha horizontal é múltiplo de 3;

c) a soma de cada linha vertical é múltiplo de 3 e 6;

d) a soma de todos os números do quadrado tem como resultado 666.

Autor: Ricardo Silva - junho/2018

Fontes Bibliográficas:

[1] Ball, W. W. Rouse - Mathematical Recreations and Essays - Macmillan and Co., Limited New york: The Macmillan Company - 1905 (Release Date: October 8, 2008 [EBook #26839])

[2] Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.

[3] Silva, Ricardo José da. Números Triangulares e Sequências Numéricas - livro digital - São Paulo, 2013

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

Matérias relacionadas:

011-estudos-169-quadrados-magicos

011-estudos-170-quadrados-magicos-ordem-3

011-estudos-171-quadrados-magicos-pitagoricos

011-estudos-172-quadrados-magicos-numeros-primos

011-estudos-173-quadrado-magico-ordem3-numero-30

011-estudos-174-quadrados-magicos-numeros-quadrados-perfeitos

011-estudos-175-quadrados-magicos-pitagoricos-e-os-numeros-3-4-5

011-estudos-176-quadrados-magicos-e-qualquer-numero

011-estudos-177-ternos-pitagoricos-e-formula-de-euclides

011-estudos-180-quadrados-magicos-bimagicos-multimagicos

011-estudos-181-quadrados-magicos-ordem3-4-5-e-numeros-quadrado-perfeitos

011-estudos-182-quadrados-magicos-pitagoricos-de-ordem-3-3-3

011-estudos-183-quadrados-magicos-pitagoricos-3-3-3-imperfeito

011-estudos-184-quadrados-magicos-ordem-4

011-estudos-185-quadrados-magicos-ordem-4-numeros-quadrados-perfeitos

011-estudos-186-quadrados-magicos-ordem-5

011-estudos-187-quadrados-magicos-de-ordem5-numeros-quadrados-perfeitos

011-estudos-188-quadrados-magicos-pitagoricos-ordem-5-5-5

NOVO LIVRO DIGITAL (E-book)

livro quadrados mágicos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

LIVRO DIGITAL (E-book) Números Triangulares e Sequências Numéricas

livro triangulares e sequências numéricas mágicas

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo deste site está protegido por direitos autorais.

O uso acadêmico e escolar está liberado, desde que informando ao autor o local ou o meio em que será utilizado e divulgado, através do e-mail: contato

O uso comercial é proibido.

curta fantasticos numeros primos no facebook

Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.

Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).

Desenvolvimento de WebSite.

Contato

ric@osfantasticosnumerosprimos.com.br

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111

						111

31	9	2	22	27	20	111
3	32	7	21	23	25	111
35	1	6	26	19	24	111
4	36	29	13	18	11	111
30	5	34	12	14	16	111
8	28	33	17	10	15	111

111	111	111	111	111	111	111