


- "Ráios duplos!"
- "Ráios duplos, Muttley!"
Este era o bordão que Dick Vigarista falava quando alguma coisa dava errada ao seu fiel (escudeiro) co-piloto Mutlley, da série de desenho animado Corrida Maluca produzido pelos estúdios Hanna-Barbera nos anos 60 e que passou na TV nos 70 aqui no Brasil.
E parafraseando Dick Vigarista:
Ternos Duplos!
Ternos Pitagóricos Duplos!
Isto mesmo, Ternos Pitagóricos Duplos, um novo grupo de ternos pitagóricos; uma sequência de ternos pitagóricos gerados pelas Fórmulas de Euclides e outra gerada por meio da construção de um conjunto de 3 Quadrados Mágicos Pitagóricos Perfeitos.
Euclides, em seu livro Elementos, demonstrou que existe uma infinidade de ternos pitagóricos primitivos. Além disso, encontrou fórmulas que geram todos os ternos pitagóricos primitivos. Dados dois números naturais m>n, o terno (a,b,c), onde:
a = m² - n²
b = 2mn
c = m² + n²
é pitagórico, e é primitivo se e somente se m e n são primos entre si e possuem paridades distintas.
Fonte: https://pt.wikipedia.org/
onde:
m > n (m tem que ser maior que n)
m e n tem que ser primos entre si
Utilizando as Fórmulas de Euclides foram gerados sequencialmente 1.000 ternos pitagóricos, entre eles, ternos primitivos e ternos derivados os quais foram classificados conforme características abaixo:
a) Ternos Pitagóricos Primitivos de Ordem Triangular;
b) Ternos Pitagóricos Primitivos de Ordem Não Triangular;
c) Ternos Pitagorícos Derivados Pares;
d) Ternos Pitagóricos Derivados Ímpares;
e) Ternos Pitagóricos Raros.
e também foram constatados que ternos pitagóricos estão estritamente relacionados com números triangulares.
Estes estudos se encontram publicados no livro digital Ternos Pitagóricos e Sequências Numéricas.
Análises realizadas no Quadrado Mágico Pitagórico Perfeito de Royal Vale Heath (1883-1960) - mágico e entusiasta matemático estadunidense, formado por um conjunto de 3 Quadrados Mágicos 3x3, constatam novas propriedades dos quadrados mágicos em si, quanto nas formações de sequências numéricas nas quais aparecerem determinados ternos pitagóricos com novas caractéristicas e que não são gerados pelas Fórmulas de Euclides.
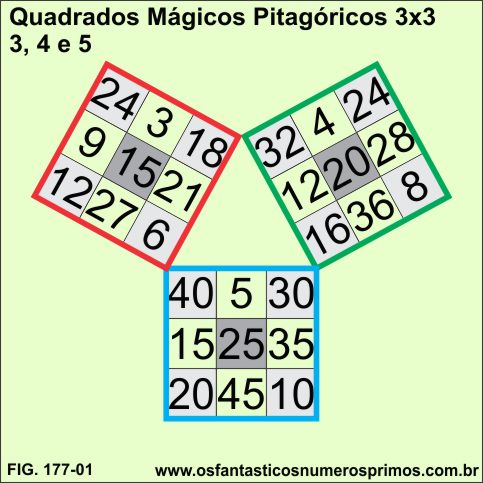
Fonte: HEATH, Royal Vale. Mathemagic: Magic, Puzzles and Games with Numbers (Dover Recreational Math) Paperback – June 1, 1953.
Ternos Pitagóricos Duplos possuem uma característica comum entre eles. As somas dos quadrados dos dois primeiros termos tem como resultado um mesmo número quadrado perfeito.
Terno Pitagórico gerado pelo conjunto de 3 Quadrados Mágicos Pitagóricos de Royal Vale Heath
Soma dos termos do quadrado vermelho = 135
Soma dos termos do quadrado verde = 180
Soma dos termos do quadrado azul = 225
Somas dos termos de cada quadrado elevado ao quadrado
(135² = 18.225)
(180² = 32.400)
18.225 + 32.400 = 50.625
(225² = 50.625)
Terno gerado pelas Fórmula de Euclides
(63² = 3.969)
(216² = 46.656)
3.969 + 46.656 = 50.625
(225² = 50.625)
Os dois ternos pitagóricos têm o mesmo resultado: 50.625
Podemos saber qual é o terno pitagórico primitivo gerador do Terno Pitagórico Derivado 135, 180, 225, através das seguintes etapas:
| Decomposição | |||
|---|---|---|---|
| em fatores primos | |||
| do Terno Pitagórico | |||
| 135, 180, 225 | |||
| Fatores Primos | |||
| 135 | 180 | 225 | 2 |
| 135 | 90 | 225 | 2 |
| 135 | 45 | 225 | 3 |
| 45 | 15 | 75 | 3 |
| 15 | 5 | 25 | 3 |
| 5 | 5 | 5 | 5 |
| 1 | 1 | 1 | |
3 x 3 x 5 = 45
mdc (135, 180, 225) = 45
135 : 45 = 3
180 : 45 = 4
225 : 45 = 5
Os termos do Terno Derivado 135, 180, 225 divididos pelo mdc=45 gera o Terno Pitagórico Primitivo 3, 4, 5.
O Terno Pitagórico Primitivo 3, 4, 5 é um terno pitagórico gerado pelas Fórmulas de Euclides.
Podemos saber qual é o terno pitagórico primitivo gerador do Terno Pitagórico Derivado 63, 216, 225, através das seguintes etapas:
| Decomposição | |||
|---|---|---|---|
| em fatores primos | |||
| do Terno Pitagórico | |||
| 63, 216, 225 | |||
| Fatores Primos | |||
| 63 | 216 | 225 | 2 |
| 63 | 108 | 225 | 2 |
| 63 | 54 | 225 | 2 |
| 63 | 27 | 225 | 3 |
| 21 | 9 | 75 | 3 |
| 7 | 3 | 25 | 3 |
| 7 | 1 | 25 | 5 |
| 7 | 1 | 5 | 5 |
| 7 | 1 | 1 | 7 |
| 1 | 1 | 1 | |
3 x 3= 9
mdc (63, 216, 225) = 9
63 : 9 = 7
216 : 9 = 24
225 : 9 = 25
Os termos do Terno Derivado 63, 216, 225 divididos pelo mdc=9 gera o Terno Pitagórico Primitivo 7, 24, 25.
O Terno Pitagórico Primitivo 7, 24, 25 é um terno pitagórico gerado pelas Fórmulas de Euclides.
Um método prático para se gerar sequências de ternos pitagóricos derivados a partir de terno pitagórico primitivo é multiplicar o terno pitagórico primitivo pela sequência de números naturais.
No exemplo o Terno Pitagórico Primitivo 3, 4, 5 multiplicado pela sequência de números naturais.
Os ternos pitagóricos (cor amarelo) são o dobro, do dobro, do dobro... do Terno Pitagórico Primitivo 3, 4, 5. que podem ser gerados pelas Fórmulas de Euclides.
Os ternos pitagóricos (cor laranja) não são gerados pelas Fórmulas de Euclides.
| Terno Pitagórico 3,4,5 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e derivados | ||||||||||||
| números naturais | ||||||||||||
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 16 | ... | 45 |
| primitivo | derivados | |||||||||||
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | .. | 48 | ... | 135 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | ... | 64 | ... | 180 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | ... | 80 | ... | 225 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||||
No exemplo o Terno Pitagórico Primitivo 7, 24, 25 multiplicado pela sequência de números naturais.
Os ternos pitagóricos (cor amarelo) são o dobro, do dobro, do dobro... do Terno Pitagórico Primitivo 7, 24, 25. que podem ser gerados pelas Fórmulas de Euclides.
Os ternos pitagóricos (cor laranja) não são gerados pelas Fórmulas de Euclides.
| Terno Pitagórico 7, 24, 25 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e derivados | ||||||||||||
| números naturais | ||||||||||||
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 16 | ... | 45 |
| primitivo | derivados | |||||||||||
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | .. | 112 | ... | 315 |
| 24 | 28 | 72 | 96 | 120 | 144 | 168 | 192 | 216 | ... | 384 | ... | 1080 |
| 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | ... | 400 | ... | 1225 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||||
O Terno Pitagórico Derivado Impar 63, 216, 225 pode ser gerado pelas Fórmulas de Euclides a partir dos números 12 e 9.
a = m² - n²
b = 2mn
c = m² + n²
a = 12² - 9²
a = 144 - 81
a = 63
b = 2 x 12 x 9
b= 219
c = 12² + 9²
c = 144 + 81
c= 225
Autor: Ricardo Silva - maio/2018
Texto atualizado em 26/04/2021.
HEATH, Royal Vale. Mathemagic: Magic, Puzzles and Games with Numbers (Dover Recreational Math) Paperback – June 1, 1953.
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato