


"Quadrados Mágicos são muito conhecidos por qualquer pessoa que já tenha se interessado por matemática recreativa. As primeiras menções que podemos encontrar datam de 3 mil anos, na China, e até hoje eles continuam intrigando curiosos e matemáticos profissionais: Martin Gardner, por exemplo, ofereceu um prêmio a quem encontrasse um quadrado mágico de ordem 3, composto apenas por números inteiros que sejam quadrados perfeitos."
O Texto acima foi transcrito do Guia do Professor - Experimento - autor: Leonardo Barrichelo e publicado pela Unicamp.

Fonte: https://en.wikipedia.org/wiki/Martin_Gardner
Martin Gardner, falecido em 2010, foi um escritor, grande especialista da obra Lewis Carrol, se interessava por micromagia, filosofia, literatura e por mais de 20 anos publicou na Revista Scientific American artigos sobre recreação matemática e que posteriormente foram transformados em livro.
Martin Gardner tinha problemas com cálculos e talvez por isso nunca tenha frequentado curso superior de Matemática, mas era um aficcionado por ela.
Ao longo da história, como Martin Gardner, tivemos muitos homens que também não eram Matemáticos de formação e contribuiram para o desenvolvimento da Matemática.
O que chama atenção na introdução do texto do Guia do Professor é o prêmio a quem conseguisse formar Quadrado Mágico de ordem 3 com números quadrados perfeitos.
Fazendo pesquisas na World Wide Web, não foi possível saber se houve algum ganhador do referido prêmio.
Será que era ou é tão difícil formar um Quadrado Mágico com tais características?
Com os 9 primeiros números quadrados perfeitos não é possível formar um Quadrado Mágico de ordem 3.
As diferenças (razões) entre os quadrados não são constantes.
| Sequência de | Razão |
| números quadrados | |
| perfeitos | (diferença |
| entre os | |
| termos) | |
| 1 | |
| 3 | |
| 4 | |
| 5 | |
| 9 | |
| 7 | |
| 16 | |
| 9 | |
| 25 | |
| 11 | |
| 36 | |
| 13 | |
| 49 | |
| 15 | |
| 64 | |
| 17 | |
| 81 | |
| www.osfantasticosnumerosprimos.com.br | |
| Quadrado Mágico | ||||
| Imperfeito 3x3 | ||||
| 93 | ||||
| 16 | 81 | 4 | 101 | |
| 9 | 25 | 49 | 83 | |
| 64 | 1 | 36 | 101 | |
| 89 | 107 | 89 | 77 | |
As somas de cada uma das linhas horizontal e vertical bem com as diagonais não apresentam como resultados Constante Mágica.
A soma de todos os números quadrados não é um quadrado perfeito.
√285 = 16,881
Reescrevendo o quadrado 3x3 com números inteiros consecutivos.
| Quadrado Mágico 3x3 | ||||
| constante mágica 15 | ||||
| 15 | ||||
| 4 | 9 | 2 | 15 | |
| 3 | 5 | 7 | 15 | |
| 8 | 1 | 6 | 15 | |
| 15 | 15 | 15 | 15 | |
Temos a Soma Mágica 45 que não é um quadrado perfeito.
√45= 6,7082
No livro The Pythagorean Propositions do Professor estadunidense Elisha Scoot Loomis, reimpressão da segunda edição de 1940, há cinco exemplos de Quadrados Mágicos Pitagóricos e na página 254 se encontra o exemplo de número dois.

Fonte: Loomis, Elisha Scott. The Pythagorean Propositions - by The National Council of Teachers of Mathematics, Inc. - 1968
Transcrevemos o quadrado HD que é um quadrado de ordem 3 e formado com números quadrados perfeitos.
As diferenças (razões) entre os quadrados não são constantes.
| Sequência de | Razão |
| números quadrados | |
| perfeitos | (diferença |
| entre os | |
| termos) | |
| 4 | |
| 21 | |
| 25 | |
| 39 | |
| 64 | |
| 57 | |
| 121 | |
| 75 | |
| 196 | |
| 93 | |
| 289 | |
| 111 | |
| 400 | |
| 129 | |
| 529 | |
| 147 | |
| 676 | |
| www.osfantasticosnumerosprimos.com.br | |
| 744 | ||||
| 196 | 25 | 64 | 285 | |
| 121 | 4 | 529 | 654 | |
| 676 | 289 | 400 | 1365 | |
| 993 | 318 | 993 | 600 |
As somas de cada uma das linhas horizontal e vertical bem como as diagonais não apresentam como resultados Constante Mágica.
A soma de todos os números quadrados é um quadrado perfeito 2304.
√2304 = 48
Reecrevendo o quadrado com números inteiros
| Quadrado Mágico | ||||
| Imperfeito 3x3 | ||||
| 36 | ||||
| 14 | 5 | 8 | 27 | |
| 11 | 2 | 23 | 36 | |
| 26 | 17 | 20 | 63 | |
| 51 | 24 | 51 | 36 | |
As somas de cada uma das linhas horizontal e vertical bem como as diagonais não apresentam como resultados Constante Mágica.
A soma de todos os números que é 126, não é um quadrado perfeito.
√126 = 11,224
Será que Martin Gardner tinha conhecimento deste feito do Professor Elisha Scoot Loomis? Porque o professor chegou quase perto de ter produzido um Quadrado Mágico 3x3 com números quadrados perfeitos.
Ou será que Martin Gardner passou horas e horas tentando produzir o tal Quadrado Mágico e não conseguindo resolveu estabelecer o tal prêmio?
Quadrado Mágico Pitagórico de Royal Vale Heath, publicado por Editora Inglesa de Passatempos, ano de 1930.
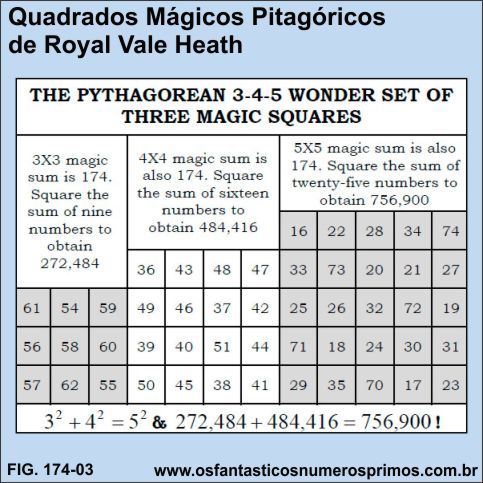
Fonte: Sparks, John C. The Pythagorean Theorem - Crown Jewel of Mathematics - by Published by AuthorHouse, 1663 Liberty Drive, Suite 200, Bloomington, Indiana, 2008.
Transcrevemos o quadrado 3x3 que é um quadrado de ordem 3 e formado com números inteiros consecutivos.
As diferenças (razões) entre os números são constante.
| Progressão | Razão |
| Aritmética | |
| (diferença | |
| entre os | |
| termos) | |
| 54 | |
| 1 | |
| 55 | |
| 1 | |
| 56 | |
| 1 | |
| 57 | |
| 1 | |
| 58 | |
| 1 | |
| 59 | |
| 1 | |
| 60 | |
| 1 | |
| 61 | |
| 1 | |
| 62 | |
| www.osfantasticosnumerosprimos.com.br | |
| Quadrado Mágico 3x3 | ||||
| constante mágica 174 | ||||
| 174 | ||||
| 61 | 54 | 59 | 174 | |
| 56 | 58 | 60 | 174 | |
| 57 | 62 | 55 | 174 | |
| 174 | 174 | 174 | 174 | |
As soma de cada linha horizontal, vertical e diagonais tem como resultado a Constante Mágica 174.
A soma de todos os números é 522.
522² = 272.484
Reescrevendo o quadrado 3x3 com números quadrados perfeitos.
| Quadrado Mágico | ||||
| Imperfeito 3x3 | ||||
| 10094 | ||||
| 3721 | 2916 | 3481 | 10118 | |
| 3136 | 3364 | 3600 | 10100 | |
| 3249 | 3844 | 3025 | 10118 | |
| 10106 | 10124 | 10106 | 10110 | |
A soma de todos os números não é quadrado perfeito 30.336
√30.336 = 174,172
Observação: a raiz quadrada é proxima a Constante Mágica do Quadrado Mágico com números inteiros.
Escolher sequências de 9 números inteiros consecutivos e elaborar Quadrados Mágicos de ordem 3x3 é simples é rápido, conhecendo as técnicas de montagem.
Escolher 16 números inteiros consecutivos e elaborar um Quadrado Mágico de ordem 4x4 é um pouco mais demorado, mas não tão complicado, mesmo conhecendo as técnicas de montagem.
Escolher 25 números inteiros consecutivos e elaborar um Quadrado Mágico de ordem 5x5 é exige mais atenção e é um pouco demorado mesmo conhecendo as técnicas de montagem.
Depois de montado, em cada Quadrado Mágico tem que se somar cada linha, cada coluna, cada uma das diagonais para verificar se o resultado da Costante Mágica é a mesma.
E ainda somar as Constantes Mágicas das linhas, colunas e diagonais para se obter a Soma Mágica.
Agora imagina tentando montar um só Quadrado Mágico de ordem 3x3 com números quadrados perfeitos em que a Constante Mágica e Soma dos Termos deva ter como resultado também número quadrado perfeito.
Com os exemplos expostos, nota-se que foram feitos grandes esforços e cálculos para se chegar a cada resultado, pois tanto em 1900 quanto em 1930, não havia ainda calculadoras, planilhas eletrônicas ou computadores pessoais que só surgiram muitas decádas depois...
Martin Gardner sabia..., sabia que era e ainda é um excelente desafio para o cérebro, e hoje para cérebros e computadores.
Autor: Ricardo Silva - maio/2018
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato