capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Quadrados Mágicos / Bimágicos / Multimágicos - 180

Acredito estarmos diante de dois fenômenos similares, similares no sentido de terem vastas demonstrações, isto é, vários modelos matemáticos: um é o brilhante Teorema de Pitágoras, o outro, o dispositivo numérico Quadrado Mágico.

Exemplos de diversas aplicações do Teorema de Pitágoras podem ser encontrados no trabalho do Professor estadunidense Elisha Scott Loomis que compilou em seu livro The Pythagorean Propositions, reimpressão da segunda edição de 1940, mais de 370 provas do Teorema de Pitágoras.

Agrupadas nas seguintes categorias:

a) Algébrica (109);

b) Geométrica (255);

c) Quaternionic (4);

d) Provas baseada em massa e velocidade, Dinâmica (2);

e) Quadrados Mágicos Pitagóricos (5).

Além dessas provas, diversos ramos das Ciências como a Física, a Astronomia, a Engenharia, etc..., támbém fazem o uso do Teorema de Pitágoras.

Citemos também que, por meio das Fórmulas de Euclides, podem ser gerados infinitos Ternos Pitagóricos e que fazem relação direta com o Teorema de Pitágoras.

O Quadrado Mágico é um dispositivo numérico formado por um quadrado quadriculado em que números são dispostos obedecendo certa ordem de tal maneira que a soma de cada uma das linhas horizontais, verticais e cada uma das linhas diagonais tenha sempre o mesmo resultado que é chamada de Constante Mágica.

Quanto a sua estrutura quadricular, isto é, a matriz onde é construído, o Quadrado Mágico pode ser classificado por ordem:

a) Ordem 3 ou 3x3 (3 linhas x 3 colunas = 9 células);

b) Ordem 4 ou 4x4 (4 linhas x 4 colunas = 16 células);

c) Ordem 5 ou 5x5 (5 linhas x 5 colunas = 25 células) e assim por diante.

Quadrado Mágico 3x3

O Quadrado Mágico Lo-Shu tem sua origem na antiga civilização chinesa e aparece documentado no Livro Os 9 capítulos da arte matemática no texto Shu Shu Shi Yu.

Posteriormente, foi transcrito para o sistema de numeração indo-arábico e se apresenta da seguinte forma.

quadrado mágico Lo Shu e o quadrado mágico 3x3 indo-arábico

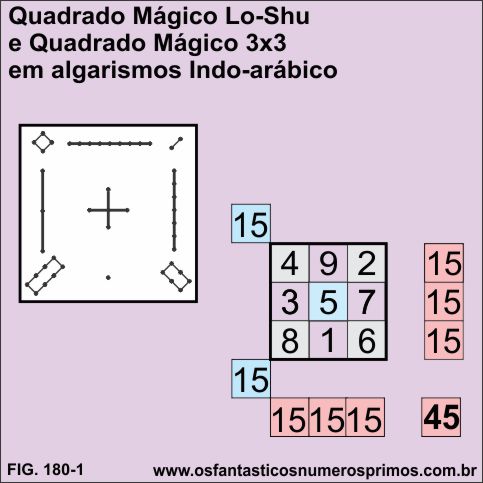
Quatro são as características principais de um Quadrado Mágico: sequência numérica, disposição dos números, a Constante Mágica e a Soma dos Termos para se elaborar um Quadrado Mágico Perfeito.

O Quadrado Mágico de 3x3 ou de ordem 3 apresentam também as seguintes propriedades:

a) a Constante Mágica (15) é o triplo do terno central (5);

b) a Constante Mágica (15) é múltiplo de 3;

c) a Soma dos Termos (45) é 3 vezes a Constante Mágica (15);

d) a Soma dos Termos (45) é 9 vezes o termo central (5);

e) a Soma do Termos (45) é 13 vezes a ordem 3;

f) a soma dos números dos vértices (2, 6, 8 ,4) é 4 vezes o termo central (5);

g) a soma dos números centrais das laterais (7, 1, 3, 9 ) é 4 vezes o termo central (5);

h) a soma de dois números dos vértices (2, 8) ou (6,4) é 2 vezes o termo central (5);

i) a soma de dois números centrais das laterais (1, 9) ou (3, 7 ) é 2 vezes o termo central (5);

Os números 1, 2, 3, 4, 5, 6, 7, 8 e 9 podem ser permutados dentro do quadriculado 362.880 vezes, mas apenas 8 combinações resultam em Quadrados Mágicos e dentre as 8 combinações, 7 Quadrados Mágicos são variações por rotação ou reflexão dos elementos.

Todas estas características do Quadrado Mágico estão fundamentadas nas propriedades de Progressão Aritmética Finita e neste exemplo foram utilizados os 9 primeiros números naturais.

Infinitos Quadrados Mágicos podem ser produzidos com infinitas Progressões Artiméticas Finitas.

Tipos de Quadrados Mágicos

Quadrado Mágico Puro / Normal / Fundamental

É o Quadrado Mágico formado pelos primeiros números inteiros de 1 a n².

O Quadrado Mágico 3 x 3 transcrito do Quadrado Mágico Lo-Shu é um exemplo de Quadrado Mágico Puro.

Quadrado Mágico Derivado

Somando-se ou subtraindo-se um número constante a cada termo do Quadrado Mágico Puro, obtem-se um Quadrado Mágico Derivado.

Quadrado Mágico composto

Por exemplo, a partir do Quadrado Mágico de ordem 3, somando-se oito constantes distintas de cada vez, obtêm-se 8 novos Quadrados Mágicos que justapondo-se ao Quadrado Mágico de ordem 3 forma-se um quadro mágico maior 9x9 ou de ordem 9.

Quadrado Mágico Multiplicativo

Muliplicando-se um número constante a cada termo do Quadrado Mágico Puro, obtem-se um Quadrado Mágico Multiplicativo cuja constante será uma Constante Mágica Multiplicativa.

Quadrados Bimágicos

Várias são as possibilidades, características e variáveis matemáticas bem como métodos diversos de se ordenar números para se construirem Quadrados Mágicos, no exemplo acima, o Milenar Menor Quadrado Mágico do Mundo, o Lo-Shu.

Eis que em 1890, há 120 anos atrás, Georges Pfeffermann, alemão naturalizado francês criou o primeiro Quadrado Bimágico de ordem 8.

Quadrado Bimágico é um quadrado que permanece mágico depois que seus números forem elevados ao quadrado e que posteriormente somados cada uma das linhas horizontais, verticais e diagonais tenham como resultado uma Constante Mágica.

Quadrado P-Multimágico é um quadrado que permanece mágico depois que seus números forem elevados a qualquer potência e que posteriormente somados cada uma das linhas horizontais, verticais e diagonais tenham como resultado uma Constante Mágica.

Quadrado Mágico 8x8 soma 260

Quadrado Mágico desenvolvido por Georges Pfeffermann

Quadrado Mágico 8x8
constante mágica 260
								260
56	34	8	57	18	47	9	31	260
33	20	54	48	7	29	59	10	260
26	43	13	23	64	38	4	49	260
19	5	35	30	53	12	46	60	260
15	25	63	2	41	24	50	40	260
6	55	17	11	36	58	32	45	260
61	16	42	52	27	1	39	22	260
44	62	28	37	14	51	21	3	260
260	260	260	260	260	260	260	260	260

Fonte: www.multimagie.com

Quadrado Bimágico 8x8 soma 11180

Quadrado Bimágico de ordem 8 (quadrado de quadrado) de Georges Pfeffermann elevando-se cada número do Quadrado Mágico acima ao quadrado.

Quadrado Bi-Mágico 8x8
constante mágica 11180

3136	1156	64	3249	324	2209	81	961
1089	400	2916	2304	49	841	3481	100
676	1849	169	529	4096	1444	16	2401
361	25	1225	900	2809	144	2116	3600
225	625	3969	4	1681	576	2500	1600
36	3025	289	121	1296	3364	1024	2025
3721	256	1764	2704	729	1	1521	484
1936	3844	784	1369	196	2601	441	9

Fonte: www.multimagie.com

Tipos de Quadrados Multimágicos

Após este feito do Sr. Georges Pfeffermann, nomenclaturas foram criadas para melhor classificarem Quadrados Multimágicos:

- Bimagic

- Trimagic

- Tetramagic

- Pentamagic

- Hexamagic

- Highly multimagic

- Magic squares of squares

- Squares of cubes

- Squares of 6th, of 7th powers

- Squares of triangular & polyg nbs

- Smallest bimagic square

- Smallest trimagic square

- Smallest tetramagic square

- Smallest pentamagic

- Bimagic squares

- Bi-trimagic squares

- Pandiagonal bi-trimagic squares

- Bimagic squares of primes

Fonte: www.multimagie.com

Como vemos, a partir do Quadrado Mágico Lo-Shu, novos tipos foram surgindo e sendo criados conforme caractéristicas comuns de suas construções e formações.

E ainda mais intrigante e interessante, é que até os dias atuais, não se conseguiu criar um Quadrado Mágico Perfeito ao quadrado de ordem 3 x 3 (Bimágico).

Este e outros problemas matemáticos não resolvidos relacionados a Quadrados Mágicos continuam em aberto esperando soluções, e melhor, quem os resolver poderá ganhar prêmios em dinheiro (Euros).

Autor: Ricardo Silva - junho/2018