Página de estudos de matemática e sequências numéricas

Quadrados Mágicos 4x4 - 184

Quadrado Mágico 4x4 ou de ordem 4 é um quadrado quadriculado formado por 4 linhas e 4 colunas perfazendo um total de 16 células.

O Quadrado Mágico de ordem 4, Normal ou Puro tem como formação os 16 primeiros números naturais (1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11, 12 , 13, 14, 15 e 16) ou 1 a n².

Albrecht Durer, em sua obra "Melancolia" de 1514, retrata uma variante de Quadrado Mágico de ordem 4 cujas disposições numéricas apresentam aspectos da obra em si quanto de sua vida em particular.

Fonte: https://pt.wikipedia.org/

wiki/Quadrado_m%C3%A1gico

Quadrado Mágico 4x4 e o Método de Moschopoulos

O Método de Manuel Moschopoulos, autor bizantino que escreveu um tratado matemático sobre quadrados mágicos baseados nos textos de Ahmed al-Buni [1], também chamado de Método Igualmente Uniforme funciona para qualquer quadrado mágico de ordem par múltiplos de 4 (4, 8, 16, 32, ...).

A técnica de construção consiste em inverter as posições dos números que estão nas diagonais.

É uma técnica bastante simples em que consiste de alguns passos:

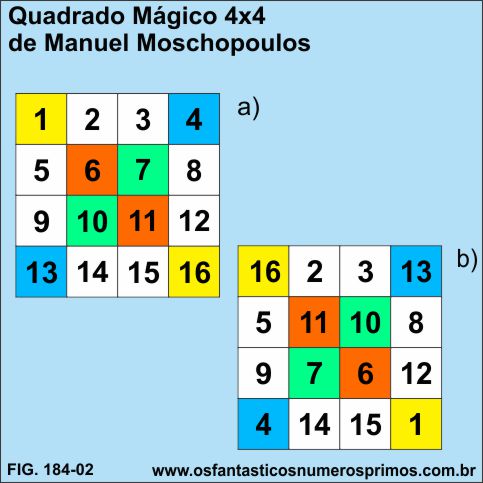
a) em um quadrado com 16 células, preencher com os números de 1 a 16, os números que estão nas células com fundo na cor branca devem ficar em posições fixas;

b) posteriormente, invertem-se as posições dos números que se encontram nas linhas diagonais do quadrado e que estão em células de fundo colorido:

o 1 troca de posição com o 16;

o 4 troca de posição com o 13;

o 6 troca de posição com o 11 e

o 7 troca de posição com 10.

Quadrado Mágico 4x4 soma mágica 34

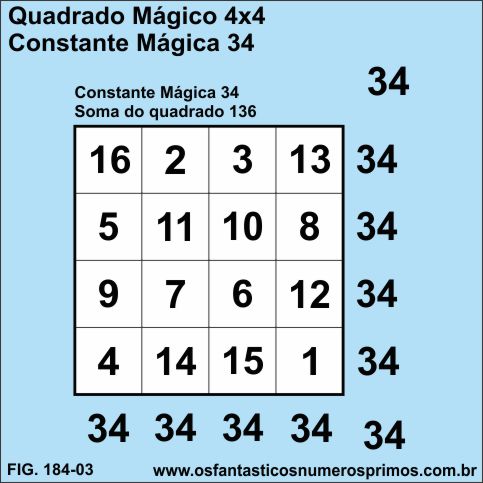
O Quadrado Mágico 4x4 tem como Constante Mágica 34 e a soma de todos os seus termos 136 com as seguintes propriedades:

a) a soma dos números das células dos cantos do quadrado tem como resultado a Constante Mágica;

16 + 13 + 1 + 4 = 34

b) a soma dos números das células do sub-quadrado superior esquerdo tem como resultado a Constante Mágica;

16 + 2 + 5 + 11 = 34

c) a soma dos números das células do sub-quadrado 2x2 inferior esquerdo tem como resultado a Constante Mágica;

9 + 7 + 4 + 14 = 34

d) a soma dos números das células do sub-quadrado 2x2 superior direito tem como resultado a Constante Mágica;

3 + 13 + 10 + 8 = 34

e) a soma dos números das células do sub-quadrado 2x2 inferior direito tem como resultado a Constante Mágica;

6 + 12 + 15 + 1 = 34

f) a soma dos números das células do sub-quadrado 2x2 central tem como resultado a Constante Mágica;

11 + 10 + 7 + 6 = 34

g) a soma dos números das células dos cantos do sub-quadrado central tem como resultado a Constante Mágica;

2 + 3 + 14 + 15 = 34

h) a soma dos números das células dos cantos do sub-retângulo tem como resultado a Constante Mágica;

16 + 3 + 9 + 6 = 34

i) a soma dos números das células dos cantos do sub-retângulo tem como resultado a Constante Mágica;

5 + 10 + 4 + 15 = 34

j) a soma dos números das células dos cantos do sub-retângulo tem como resultado a Constante Mágica;

2 + 13 + 7 + 12 = 34

k) a soma dos números das células dos cantos do sub-retângulo tem como resultado a Constante Mágica;

11 + 8 + 14 + 1 = 34

l) a soma dos números das células dos laterais centrais tem como resultado a Constante Mágica;

5 + 9 + 8 + 12 = 34

m) a soma dos números de diagonais quebradas tem como resultado a Constante Mágica;

5 + 2 + 15 + 12 = 34

n) a soma dos números de diagonais quebradas tem como resultado a Constante Mágica;

9 + 14 + 3 + 8 = 34

Permutação dos sub-quadrados 2x2 (4 células)

Os sub-quadrados 2x2 tem a soma de todos os seus números 34, que é a Constante Mágica.

Permutando os sub-quadrados, a Constante Mágica e a soma de todos os números do Quadrado Mágico de ordem 4 não se alteram.

Veja alguns exemplos:

a)

b)

c)

d)

Quadrado Mágico 4x4 e números quadrados perfeitos

Elevando-se os números de 1 a 16 do Quadrado Mágico 4x4 ao quadrado, obtem-se um Quadrado Mágico Imperfeito com as sequintes características:

a) a soma dos números quadrados perfeitos da primeira linha é igual a soma dos quadrados da quarta linha;

b) a soma dos números quadrados perfeitos da segunda linha é igual a soma dos quadrados da terceira linha;

c) a soma dos números quadrados perfeitos da primeira coluna é igual a soma dos quadrados da quarta coluna;

d) a soma dos números quadrados perfeitos da segunda coluna é igual a soma dos quadrados da terceira coluna.

Quadrado Mágico 4x4 e números cúbicos

Elevando-se os números de 1 a 16 do Quadrado Mágico 4x4 ao cubo, obtem-se um Quadrado Mágico Imperfeito com as sequintes características:

a) a soma dos números cúbicos das diagonais...

5.644 + 3.604 = 9.248

... é igual a soma dos cubos do números centrais das laterais esquerda e direita bem como das partes inferior e superior.

8 + 27 + 125 + 512 + 729 + 1728 + 2744 + 3375 = 9.248

b) a soma dos números cúbicos do quadrado 18.496 é o dobro da soma dos números das diagonais 9.248.

18.496 : 2 = 9.248

O quadrado 4x4 e números consecutivos

No livro Sequências Numéricas Magicas [2] estão publicados vários estudos sobre relações numéricas entre figuras geométricas, números figurados, naturais, quadrados, cúbicos, etc.

Em um desses estudos, os 16 primeiros números naturais são dispostos sequencialmente dentro de um quadrado 4x4 apresentando entre outras, as seguintes propriedadas numéricas:

a) as diagonais tem como resultado a Constante Mágica 34;

b) a soma de cada das linha horizontal não é múltiplo de 4;

c) a soma de cada coluna tem como resultado um múltiplo de 4;

d) a soma de todos os números do quadrado tem como resultado a Soma Mágica 136.

Autor: Ricardo Silva - julho/2018

Fontes Bibliográficas:

[1] https://www.maa.org/press/

periodicals/convergence/

the-magic-squares-of-manuel-moschopoulos-the-mathematics-of-the-methods-evenly-even-squares

[2] Silva, Ricardo José da - Sequências Numéricas Mágicas/Ricardo José da Silva - livro digital - São Paulo, 2013

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

Matérias relacionadas:

011-estudos-169-quadrados-magicos

011-estudos-170-quadrados-magicos-ordem-3

011-estudos-171-quadrados-magicos-pitagoricos

011-estudos-172-quadrados-magicos-numeros-primos

011-estudos-173-quadrado-magico-ordem3-numero-30

011-estudos-174-quadrados-magicos-numeros-quadrados-perfeitos

011-estudos-175-quadrados-magicos-pitagoricos-e-os-numeros-3-4-5

011-estudos-176-quadrados-magicos-e-qualquer-numero

011-estudos-177-ternos-pitagoricos-e-formula-de-euclides

011-estudos-180-quadrados-magicos-bimagicos-multimagicos

011-estudos-181-quadrados-magicos-ordem3-4-5-e-numeros-quadrado-perfeitos

011-estudos-182-quadrados-magicos-pitagoricos-de-ordem-3-3-3

011-estudos-183-quadrados-magicos-pitagoricos-3-3-3-imperfeito

NOVO LIVRO DIGITAL (E-book)

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.