


Triângulo de Pascal, também denominado de Triângulo de Yang Hui, Triângulo de Tartaglia é um dispositivo numérico formado por sequências numéricas que possuem diversas propriedades matemáticas relacionadas entre si como também a números figurados, números binomiais, números combinatórios, potências, geometria, entre outros.
Partes deste estudo se encontram publicados no livro digital Números Perfeitos e Sequências Numéricas e aqui são apresentadas novas conexões relacionadas a números triangulares, números tetraédricos no Triângulo de Pascal com números perfeitos.
O Triângulo de Pascal é construído da seguinte forma:
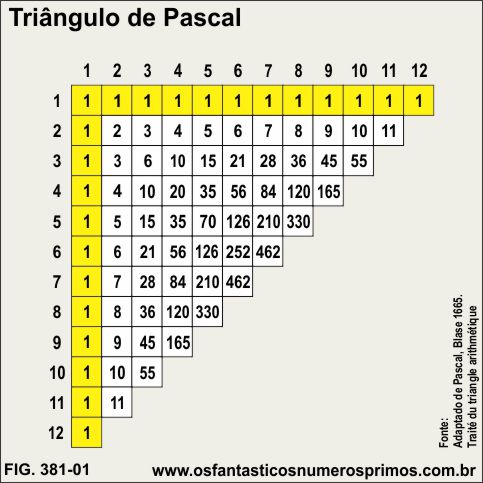
a) repete-se o número 1 nas células da primera linha e da primeira coluna;
b) soma-se dois números em sentido horizontal e coloca-se o resultado na célula abaixo;
c) ou soma-se dois números em sentido diagonal e coloca-se o resultado na célula abaixo;
d) a medida que essas somas são realizadas, começam a serem formadas as sequência numéricas.
Para mais informações, veja abaixo, matérias relacionadas.
No Triângulo de Pascal, cada sequência numérica vai sendo formada em duplicidade, isto é, uma aparece em sentido horizontal e a outra em sentido vertical.
Na coluna 2 e linha 2 - sequência de números naturais (células verde).
Na coluna 3 e linha 3 - sequência de números triangulares (células azul).
Na coluna 4 e linha 4 - sequência de números tetraédricos (células laranja).
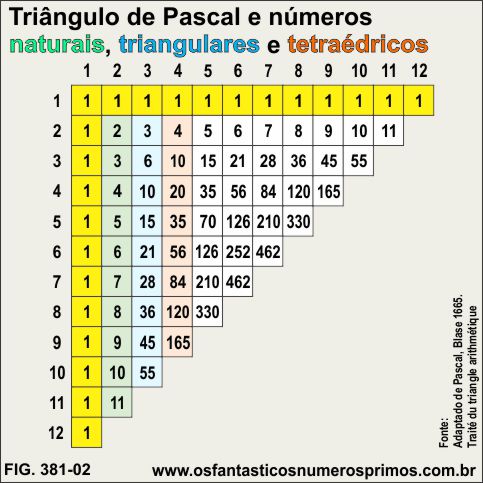
Números triangulares são números que podem ser formados por meio de arranjos de pontos formando figuras geométricas de triângulos.
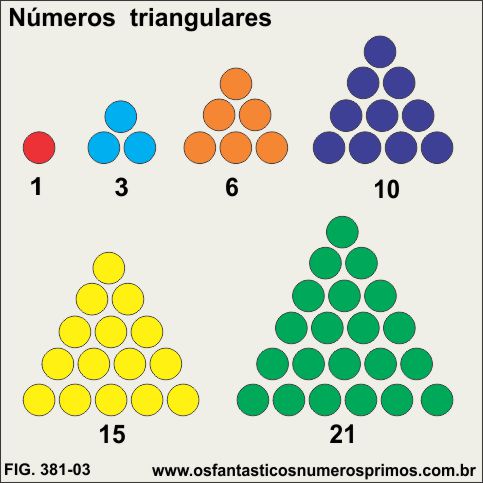
Podemos obter números triangulares por meio da soma de números naturais consecutivos começando pelo 1.
No Triângulo de Pascal, em qualquer coluna, somando-se sequências a partir de 1 até determinada linha, o resultado se encontra na coluna ao lado.
Exemplos:
Coluna 2 (cor verde ) - números naturais.
a) 1 + 2 = 3
o resultado 3 se encontra na coluna dos números triangulares ao lado (cor azul).
b) 1 + 2 + 3 = 6
o resultado 6 se encontra na coluna dos números triangulares ao lado (cor azul).
Números triangulares também podem ser obtidos pela seguinte fórmula:
| n x ( n + 1) |
| _________ |
| 2 |
onde o produto de dois números consecutivos dividido por tem como resultado um número triangular.
Exemplos:
(1 x 2) / 2 = 1
(2 x 3) / 2 = 3
(3 x 4) / 2 = 6
Um número tetraédico ou número piramidal triangular é um número figurado que pode ser representado por uma pirâmide com uma base e três lados, isto é, um tetraedro.

No Triângulo de Pascal, somando-se sequências a partir de 1 na coluna 3 (números triangulares) até determinada linha, o resultado que é um número tetraédrico se encontra na coluna ao lado (cor laranja).
Exemplos:
Coluna 3 (cor azul ) - números triangulares.
a) 1 + 3 = 4
o resultado 4 se encontra na coluna dos números tetraédricos ao lado (cor laranja).
b) 1 + 3 + 6 = 10
o resultado 10 se encontra na coluna dos números tetraédricos ao lado (cor laranja).
Números tetraédricos também podem ser obtidos pela seguinte fórmula:
| 1 x n x ( n + 1) x ( n + 2) |
| __________________ |
| 6 |
onde o produto de três números consecutivos dividido por 6 tem como resultado um número tetraédrico.
Exemplos:
(1 x 2 x 3) / 6 = 1
(2 x 3 x 4) / 6 = 4
(3 x 4 x 5) / 6 = 10
Potências de base 2 possuem uma característica especial, pois a soma dos seus divisores próprios é 1 unidade menor que essa potência, isto é, é o seu próprio antecessor.
Sendo o antecessor um número primo (Primo de Mersenne) e este multiplicado pelo seu sucessor (potência de base 2) e posteriormente dividido 2, o quociente é um número perfeito.
Por meio da expressão:
| 2n - 1 |
pode-se gerar um Número de Mersenne.
Observação importante: nem todos os Números de Mersenne são primos.
20 = 1
21 = 2
Divisor próprio: 1
Soma do divisor próprio é o próprio 1.
22 = 4
Divisores próprios: 1, 2
Soma dos divisores próprios: 1 + 2 = 3 (Primo de Mersenne)
(3 x 4) / 2 = 6 (número perfeito)
23 = 8
Divisores próprios: 1, 2, 4
Soma dos divisores próprios: 1 + 2 + 4 = 7 (Primo de Mersenne)
(7 x 8) / 2 = 28 (número perfeito)
25 = 32
Divisores próprios: 1, 2, 4, 8, 16,
Soma dos divisores próprios: 1 + 2 + 4 + 8 + 16 = 31 (Primo de Mersenne)
(31 x 32) / 2 = 496 (número perfeito)
Números perfeitos são números cuja soma de seus divisores, excetuando-se o próprio número, tem como resultado esse número.
Os 7 primeiros números perfeitos são:
1) 6;
2) 28;
3) 496;
4) 8.128;
5) 33.550.336;
6) 8.589.869.056;
7) 137.438.691.328.
Os números perfeitos estão estritamente ligados a números primos, números triangulares, potências de base 2 e números quase-potências de base 2 (números quase-perfeitos).
Veremos também novas conexões entre números perfeitos e números tetraédricos na estrutura do Triângulo de Pascal.
O número 28 é o segundo número perfeito.
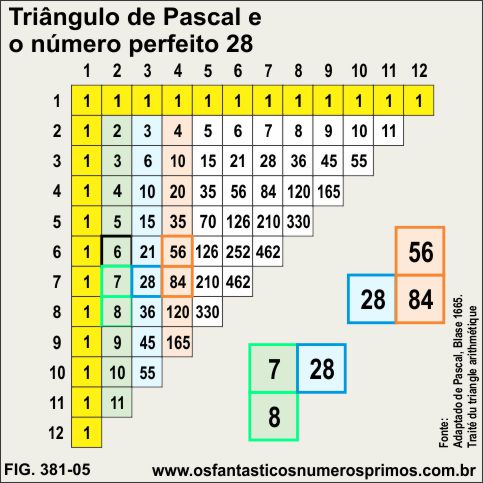
A soma dos 7 primeiros números naturais tem como resultado o número 28.
28 é 70 número triangular e perfeito.
O número triangular 28 é divisível por 7, aliáis, número triangular de ordem / posição ímpar é múltiplo dessa ordem / posição ímpar.
A soma dos 6 primeiros número tetraédricos é 56.
O número tetraédrico 56 é múltiplo de 7 e 28.
A soma dos 8 primeiros número tetraédricos é 84.
O número tetraédrico 84 é múltiplo de 7 e de 28.
O número 7 é um Primo de Mersenne.
O número 8 é sucessor de 7 e uma potência de base 2.
O produto 7 x 8 dividido por 2 gera o número perfeito 28.
O número 496 é o terceiro número perfeito.
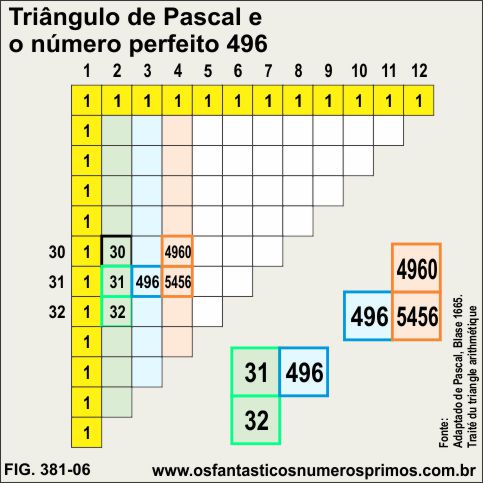
A soma dos 31 primeiros números naturais tem como resultado o número 496.
496 é 30 número triangular e perfeito.
O número triangular 496 é divisível por 31, aliáis, número triangular de ordem / posição ímpar é múltiplo dessa ordem / posição ímpar.
A soma dos 30 primeiros número tetraédricos é 4960.
O número tetraédrico 4960 é múltiplo de 31 e 496.
A soma dos 31 primeiros número tetraédricos é 5456.
O número tetraédrico 5456 é múltiplo de 31 e de 496.
O número 31 é um Primo de Mersenne.
O número 32 é sucessor de 31 e uma potência de base 2.
O produto 31 x 32 dividido por 2 gera o número perfeito 496.
O número 8.128 é o quarto número perfeito.
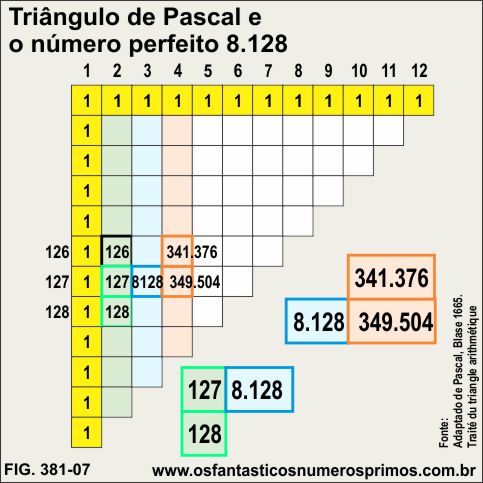
A soma dos 127 primeiros números naturais tem como resultado o número 8.128.
8.128 é 40 número triangular e perfeito.
O número triangular 8.128 é divisível por 127, aliáis, número triangular de ordem / posição ímpar é múltiplo dessa ordem / posição ímpar.
A soma dos 126 primeiros número tetraédricos é 341.376.
O número tetraédrico 341.376 é múltiplo de 127 e 8.128.
A soma dos 127 primeiros número tetraédricos é 349.504.
O número tetraédrico 349.504 é múltiplo de 127 e 8.128.
O número 127 é um Primo de Mersenne.
O número 128 é sucessor de 127 e uma potência de base 2.
O produto 127 x 128 dividido por 2 gera o número perfeito 8.128.
Autor: Ricardo Silva - maio /2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato