


Elaborando estudos referente a Quadrado Inscrito em Quadrado, o Sr. Aristóteles de Araújo Costa, Entusiasta Matemático, residente na Cidade de Teresina - Piauí, enviou a seguinte demonstração geométrica...
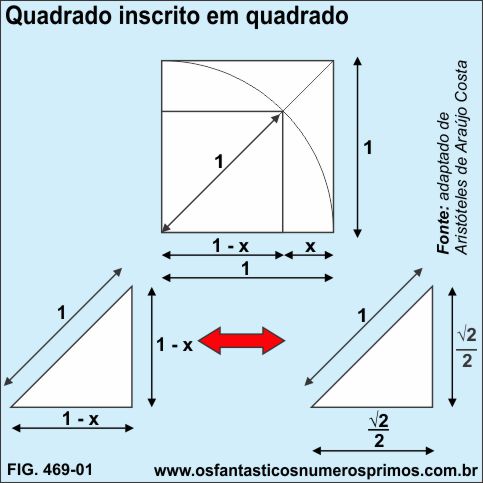
... a qual foi analisada e demonstrando realmente que em um quadrado de lado 1, traçando-se um arco de circunferência, este intersecta a diagonal, originando dois seguimentos: um de 1 unidade (número inteiro) e o outro 0,4141..., um número decimal, conforme Fig. 469-02.
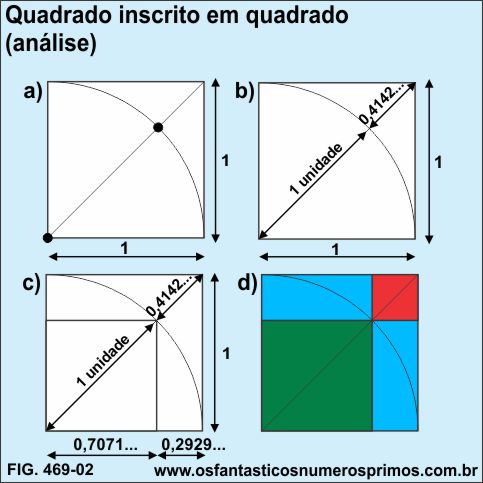
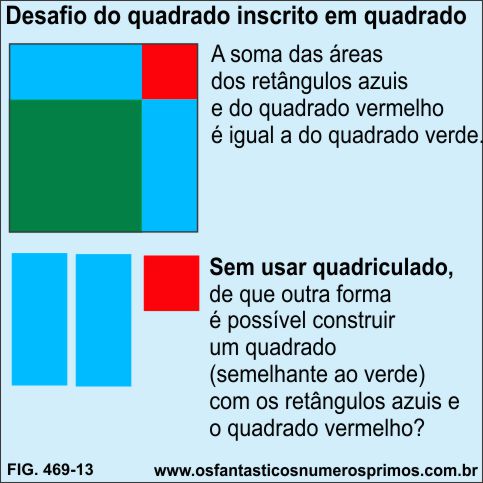
Cálculos numéricos foram efetuados, constando-se que o quadrado inscrito tem a mesma área das partes remanescentes: o quadrado vermelho e os dois retângulos azuis.
Veja baixo, matérias relacionadas, para mais informações!
Na Figura 469-03, detalhe d), a construção geométrica do Quadrado Inscrito se assemelha a construção geométrica utilizada para se explicar conceitos de Produtos Notáveis (Quadrado de uma Soma e Quadrado de uma Diferença), matéria esta que faz parte do curriculum do Oitavo Ano do Ensino Fundamental.
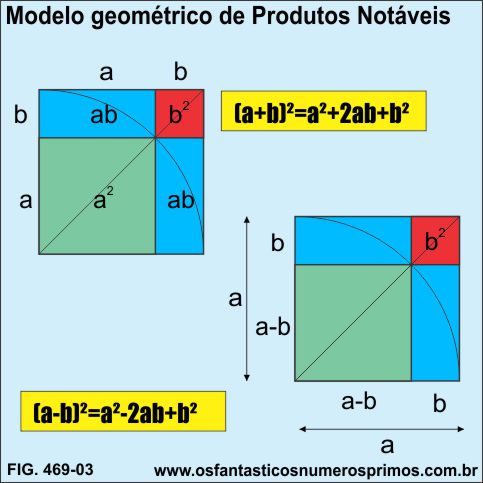
Os cálculos numéricos comprovam que a área do quadrado inscrito (verde) é a mesma dos 2 retângulos (azuis) com a do quadrado menor (vermelho).
Através de várias superposições dos retangulos (azuis) e decomposições do quadrado menor e decomposições de ambas figuras, tentou-se reconstruir um quadrado semelhante ao quadrado inscrito (verde), e por incrível que pareça, faltava sempre um "pedaço".
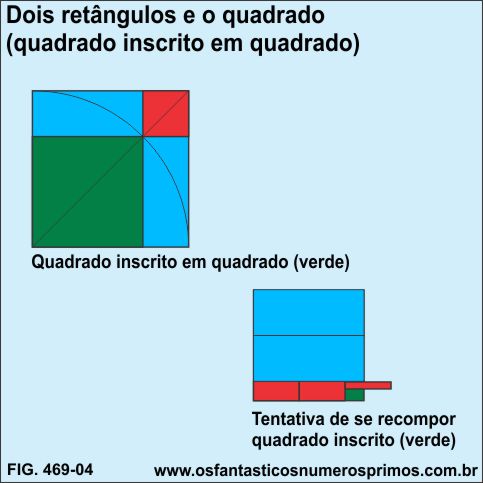
Fez-se outra tentativa de se recompor o quadrado inscrito (verde) com as áreas dos retângulos (azuis) e do quadrado menor (vermelho), conforme etapas a seguir:
a) prolongou-se o lado direito do quadrado original;
b) fez-se uma régua graduada;
c) com o ponto zero (0) sobre o vértice esquerdo inferior (mira verde) do quadrado, foi-se inclinando a régua em sentido anti-horário, até que marcações da régua sobrepusessem os limites do quadrado inscrito e do quadrado original (miras verdes);
d) desta forma o quadrado original, ficou dividido em 41 partes verticalmente;
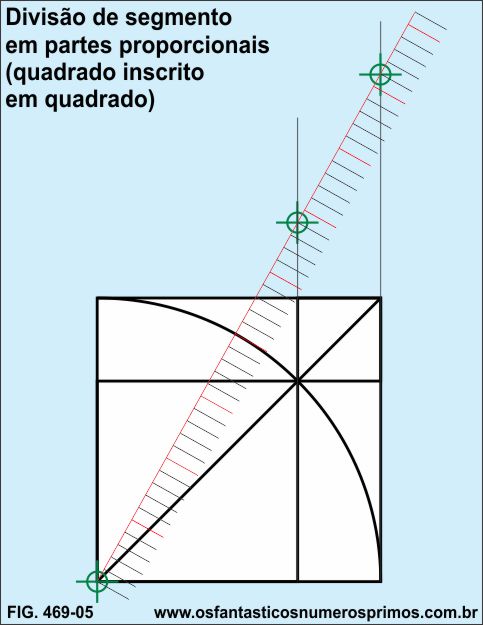
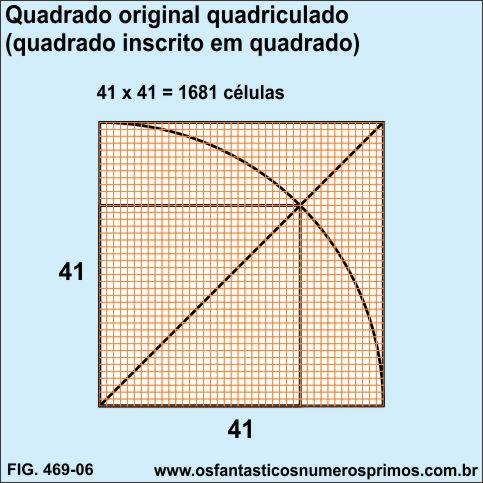
e) fez se um quadrado quadriculado de 41 x 41 células = 1681 células.
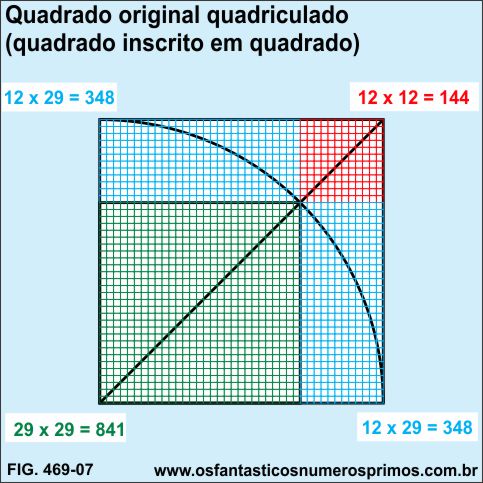
f) coloriu-se as células referente as áreas dos retângulos (azuis), do quadrado inscrito (verde) e do quadrado menor (vermelho), bem como, os cálculos de suas respectivas áreas;
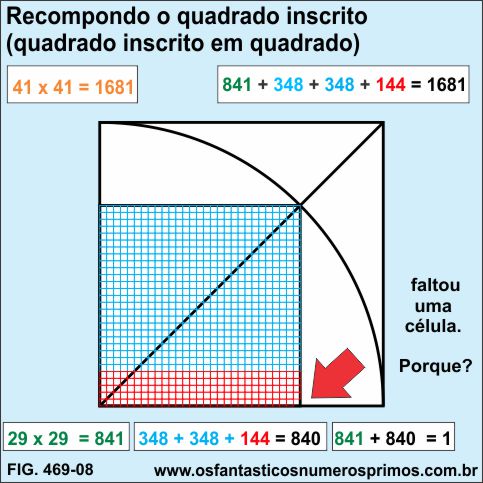
g) o quadrado inscrito foi recomposto e faltou 1 célula.
E as perguntas que ficam são:
Porquê faltou 1 célula?
Qual é a explicação lógica para tal fato?
Quadruplicando-se o Triângulo Pitagórico 3-4-5 e construindo um Modelo Geométrico de Comparação de Áreas, o quadrado inscrito (pontilhado) têm seus lados medindo 5cm (mesma medida da hipotenusa do Triângulo Pitagórico 3-4-5) e a sua diagonal, 7cm (um número inteiro que é a soma do catetos 3 e 4).
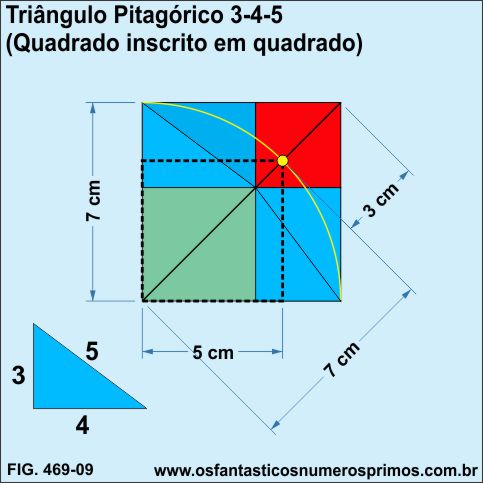
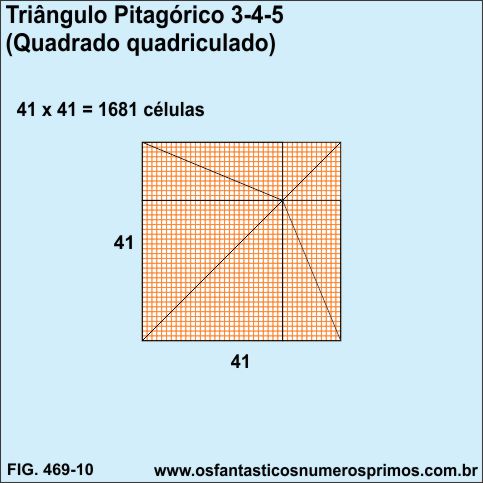
Quadriculando-se o quadrado formado a partir de 4 Triângulos Pitagóricos 3-4-5 têm se 1681 células (41 x 41).
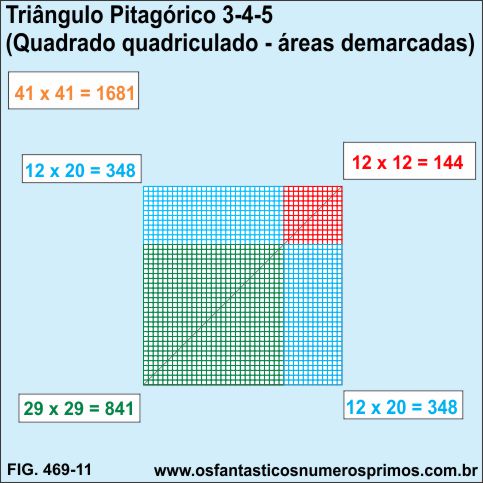
Demarcando-se as áreas dos dois retângulos (azuis), do quadrado inscrito (verde) e do quadrado menor (vermelho), têm-se:
348 células - primeiro retângulo;
348 células - segundo retângulo;
144 células - quadrado menor;
841 células - quadrado inscrito.
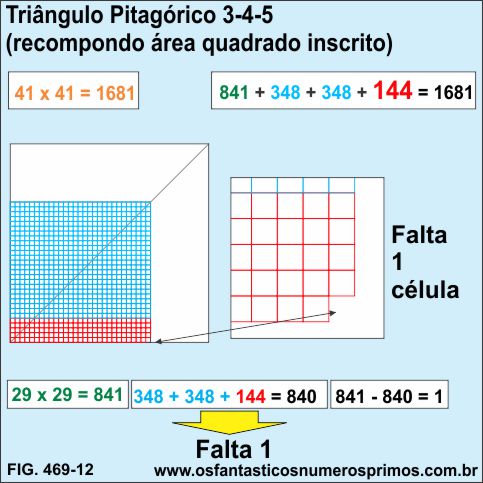
Recompondo a área do quadrado inscrito (verde) com as células dos dois retângulos e do quadrado menor, fica fantando 1 célula, isto é, 1 unidade.
E as perguntas que ficam são:
Porquê faltou 1 célula (1 unidade)?
Qual é a explicação lógica para tal fato?
O WebSite Os Fantásticos Números Primos deixa o seguinte desafio geométrico a você, estimado, visitante.
Autor: Ricardo Silva - outubro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato