


O estudo Triângulo Pitagórico e Quadrado Inscrito em Quadrado tem como base Quadrado de Diagonal 1 Inscrito em Quadrado de Lado 1, estudo este, elaborado pelo Sr. Aristóteles de Araújo Costa, Entusiasta Matemático, residente na Cidade de Teresina - Piauí.
Construindo-se quadrados com triângulos pitagóricos semelhantes à construção geométrica por comparação de áreas para se demonstrar o Teorema de Pitágoras, os Quadrados Inscritos em Quadrados apresentam um fato geométrico inusitado: de que um quadrado quadriculado cujos lados são 41 células se encaixam perfeitamente nas outras construções geométricas de Quadrados Inscritos em Quadrados gerados de triângulos pitagóricos.
Para mais informações, veja abaixo, matérias relacionadas!
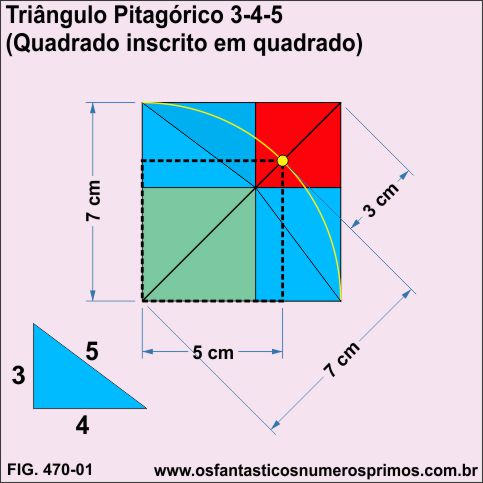
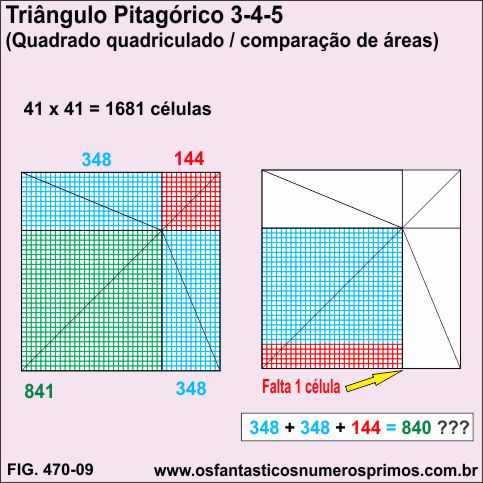
Quadruplicando-se o Triângulo Pitagórico 3-4-5 e construindo um Modelo Geométrico de Comparação de Áreas, o quadrado inscrito (pontilhado) têm seus lados medindo 5cm (mesma medida da hipotenusa do Triângulo Pitagórico 3-4-5) e a sua diagonal, 7cm (um número inteiro que é a soma do catetos 3 e 4).
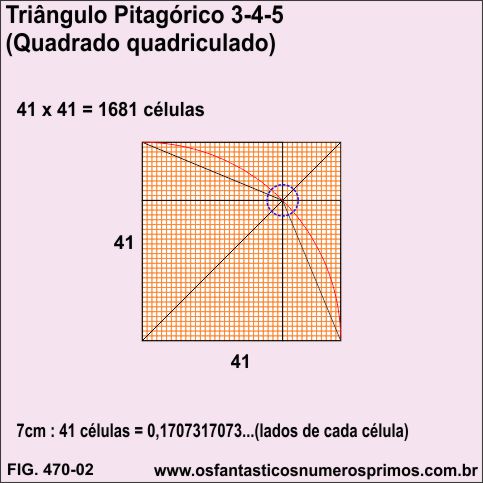
Quadriculando-se o quadrado formado a partir de 4 Triângulos Pitagóricos 3-4-5 têm se 1681 células (41 x 41).
O quadriculado se alinha perfeitamente na intersecção da diagonal principal com o arco de circunferência, bem como, com os um dos vértices dos retângulos e dos quadrados pequeno e médio.
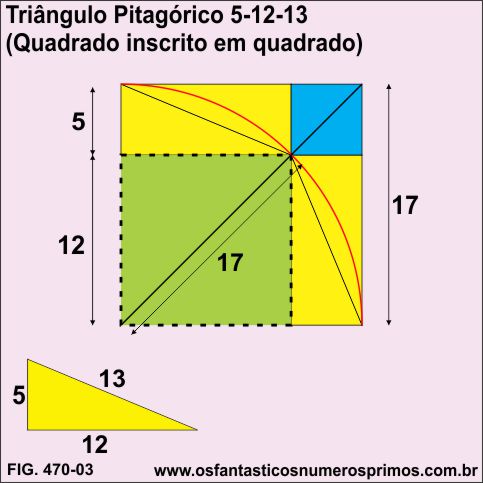
Quadruplicando-se o Triângulo Pitagórico 5-12-13 e construindo um Modelo Geométrico de Comparação de Áreas, o quadrado inscrito (pontilhado) têm seus lados medindo 12cm (mesma medida do cateto maior do Triângulo Pitagórico 5-12-13) e a sua diagonal, 17cm (um número inteiro que é a soma do catetos 5 e 12).
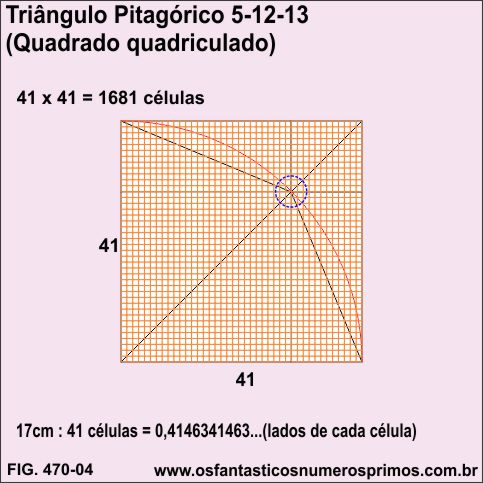
Quadriculando-se o quadrado formado a partir de 4 Triângulos Pitagóricos 5-12-13 têm se 1681 células (41 x 41).
O quadriculado se alinha perfeitamente na intersecção da diagonal principal com o arco de circunferência, bem como, com os um dos vértices dos retângulos e dos quadrados pequeno e médio.
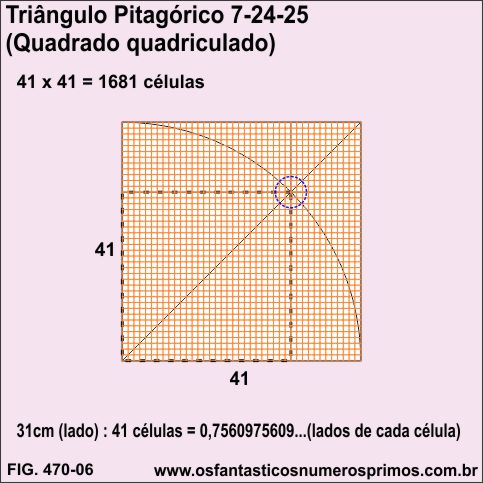
Quadruplicando-se o Triângulo Pitagórico 7-24-25 e construindo um Modelo Geométrico de Comparação de Áreas, o quadrado inscrito (pontilhado) têm seus lados medindo 22cm e a sua diagonal, 31cm (um número inteiro que é a soma do catetos 7 e 24).
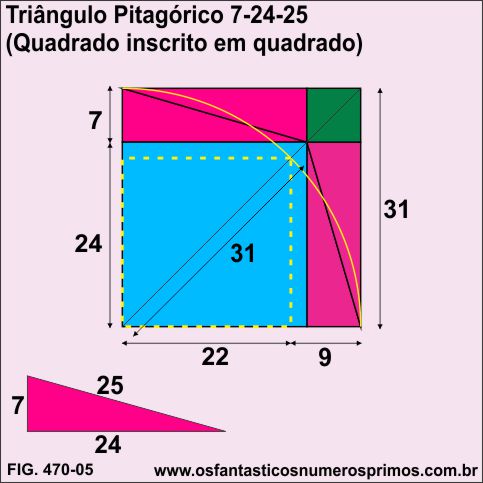
Quadriculando-se o quadrado formado a partir de 4 Triângulos Pitagóricos 7-24-25 têm se 1681 células (41 x 41).
O quadriculado se alinha perfeitamente na intersecção da diagonal principal com o arco de circunferência, bem como, com os um dos vértices dos retângulos e dos quadrados pequeno e médio.
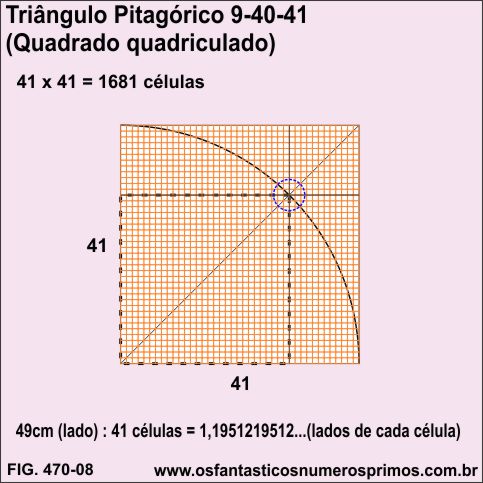
Quadruplicando-se o Triângulo Pitagórico 9-40-41 e construindo um Modelo Geométrico de Comparação de Áreas, o quadrado inscrito (pontilhado) têm seus lados medindo 35cm e a sua diagonal, 49cm (um número inteiro que é a soma do catetos 9 e 40).
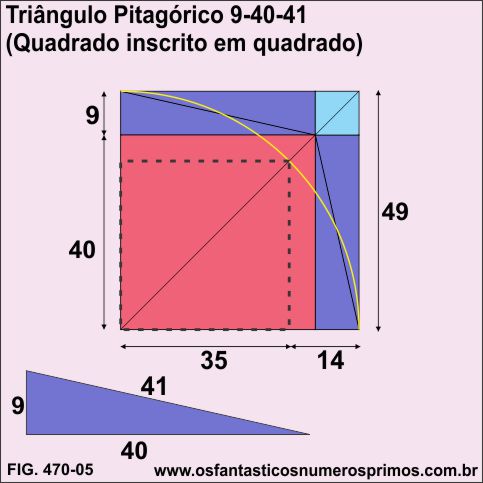
Quadriculando-se o quadrado formado a partir de 4 Triângulos Pitagóricos 9-40-41 têm se 1681 células (41 x 41).
O quadriculado se alinha perfeitamente na intersecção da diagonal principal com o arco de circunferência, bem como, com os um dos vértices dos retângulos e dos quadrados pequeno e médio.
No quadrado construído a partir de Triângulo Pitagórico 3-4-5, demarcando-se as áreas dos dois retângulos (azuis), o quadrado menor (vermelho), bem como, o quadrado inscrito (verde) e elaborando-se comparação de áreas por meio de quadriculados, percebe-se que:
a) a soma das áreas dos retângulos (azuis) e do quadrado menor (vemelho) diferem da área do quadrado inscrito (verde);
b) falta 1 quadradinho na comparação de áreas;
c) realizando-se cálculos algébricos, aritméticos ou mesmo o Teorema de Pitágoras, os resultados são corretos.
O quadriculado 41 x 41 se encaixam em todos os exemplos construídos, desde quadrados cujos lados estão em progressão geométrica (razão 2), bem como, nos exemplos construídos com triângulos pitagóricos;
Será o fato do quadrado ser um figura geométrica regular e todas as figuras que estiverem inscritas em seu interior e quando quadriculadas, sempre haverá a diferença de 1 quadradinho, isto é, 1 unidade?
A pergunta que fica é: porquê faltou 1 unidade?
Autor: Ricardo Silva - outubro/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato