


Números pares são números que ao serem divididos por 2 deixam resto 0 (zero), isto é, a divisão é exata, diferentemente, números ímpares divididos por 2 deixam resto 1 (um).
Por exemplo, 4 balas divididas entre duas crianças, cada criança, receberá, portanto, 2 balas cada uma.
2 é um número inteiro que está representando dois objetos, isto é, 2 balas.
Pense, agora, nas seguintes situações:
a) dividindo-se um círculo ao meio, obtêm-se 2 semi-círculos, mas não 2 círculos de mesmas áreas;
b) dividindo-se um quadrado ao meio, pelo ponto médio das laterais esquerda ou direita; do topo ou da base, obtêm-se 2 retângulos, mas não 2 quadrados de mesmas áreas.
c) dividindo-se um quadrado pela diagonal principal ou pela diagonal secundária, obtêm-se 2 triângulos, mas não 2 quadrados de mesmas áreas.
Nos estudos:
011-estudos-115-quadrados-dinamicos
são apresentados diversos métodos de construções geométricas em que se geram quadrados dinâmicos e proprorcionais.
O presente estudo demonstra um método de quadrado inscrito em quadrado, cuja área do quadrado inscrito é a metade do quadrado principal, bem como, da área remanescente.
Recentemente, recebi do Sr. Aristóteles de Araújo Costa, Entusiasta Matemático, residente na Cidade de Teresina - Piauí, a seguinte demonstração geométrica...
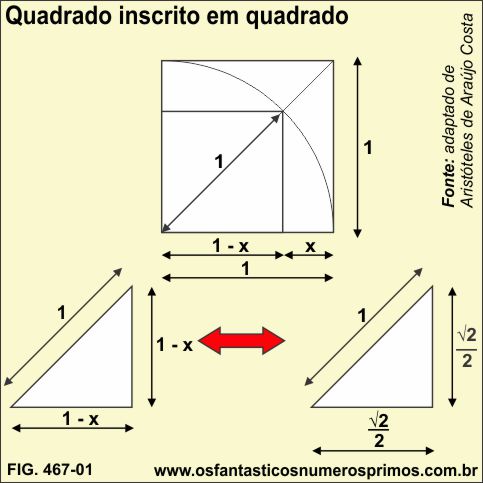
e os cálculos algébricos...
(i)
12 = ( 1 - x )2 + ( 1 - x )2
(ii)
1 = 2 ( 1 - 2x + x2 )
(iii)
2x2 - 4x + 2 - 1 = 0
(iv)
2x2 - 4x + 1 = 0
(v)
Δ = 8
(vi)
√Δ = 2 √2
(vii)
| √2 | |||
| x ' | = | 1 + | ___ |
| 2 |
(viii)
| √2 | |||
| x " | = | 1 - | ___ |
| 2 |
O interessante na demonstração é que a partir de um quadrado de lados 1, gera um quadrado inscrito cuja a diagonal também é 1 unidade, isto é, um número inteiro.
O quadrado inscrito de diagonal 1 é metade da área do quadrado principal.
Reconstruindo em um software de desenho vetorial o quadrado principal e o quadrado inscrito, nota-se que o arco de circunferência intersecta a diagonal do quadrado de lados 1, dividindo-a exatamente em um segmento de 1 unidade e o outro de 0,4142..., vejamos:
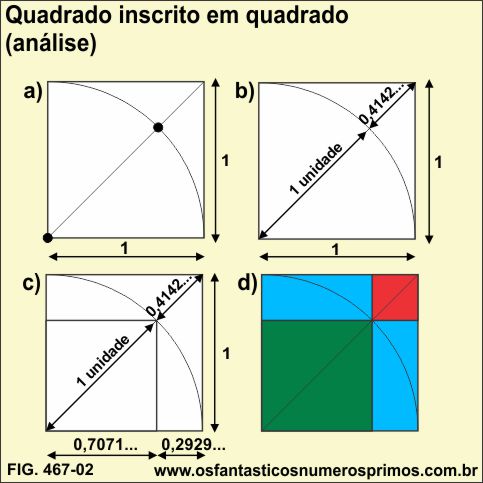
a) desenha-se um quadrado de lados 1 unidade e sua diagonal;
b) centro no vértice esquerdo inferior, traça-se um arco;
c) o arco corta a diagonal em dois seguimentos: o maior exatamente em 1 unidade (número inteiro) de comprimento, e o menor em 0,4142...(número decimal);
d) desenha-se outro quadrado até a intersecção do arco com a diagonal;
e) agora tem-se um quadrado médio de diagonal 1 unidade (número inteiro) e lados 0,7071... (número decimal), isto é, os lados medem exatamente a metade da raiz quadrada de 2;
f) prolongando-se o topo e a lateral direita do quadrado inscrito a partir do vértice direito superior, formam-se dois retângulos e um quadrado menor;
g) cálculos aritméticos:
√2 = 1,414
√2 / 2 = 0,707
0,7071...2 + 0,7071...2 =
= 0,5 + 0,5 = 1 (diagonal do quadrado médio)
A área do quadrado inscrito é a metade do quadrado original.
0,7071... x 0,7071... =
| 0,5 |
0,29289321881345247559915563789515 x
0,707
= 0,207
0,292
0,707
= 0,20710678118654752440084436210485...
0,292
0,292
= 0,085
A soma das áreas remanescentes, isto é, dos dois retângulos e do quadrado menor é a mesma do quadrado inscrito, bem como, a metado do quadrado original.
0,207
+
0,207
+
0,085
=
| 0,5 |
Os cálculos aritméticos comprovam que um quadrado inscrito em um quadrado de lados unitário tem sua área a metade do quadrado principal conforme o método geométrico aqui apresentado.
Na Figura 467-02, detalhe d), a construção geométrica é semelhante a utilizada para se explicar conceitos de Produtos Notáveis (Quadrado de uma Soma e Quadrado de uma Diferença), matéria esta que faz parte do curriculum do Oitavo Ano do Ensino Fundamental.
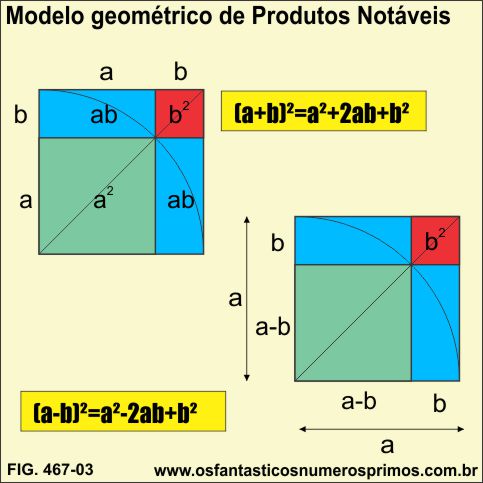
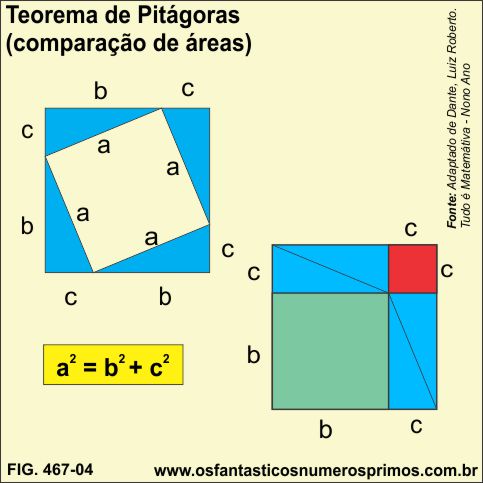
"Segundo historiadores a demonstração de Pitágoras deve ter sido uma demonstração geométrica semelhante a que segue". As duas regiões quadradas têm lados (b + c). Logo, têm a mesma área. Retirando das duas as quatro regiões triangulares congruentes, o que sobra na primeira (a²) é igual a que sobra na segunda (b² + c²).[1]
Quadruplicando-se o Triângulo Pitagórico 3-4-5 e construindo um Modelo Geométrico de Comparação de Áreas, o quadrado inscrito (pontilhado) têm seus lados medindo 5cm (mesma medida da hipotenusa do Triângulo Pitagórico 3-4-5) e a sua diagonal, 7cm (um número inteiro que é a soma do catetos 3 e 4).
Importante observar que o arco de circunferência intersecta a diagonal do quadrado maior, dividindo-a em um seguimento de 7cm e o outro de 3cm (números inteiros).
Portanto, a diagonal do quadrado de lados 7cm mede 10cm.
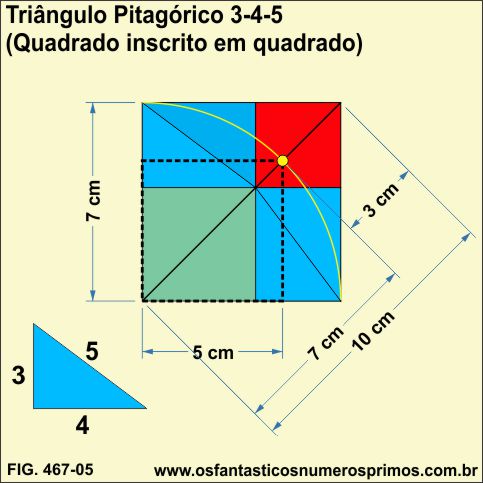
Efetuando cálculos com o Teorema de Pitágoras do quadrado pontilhado de lados 5cm:
d2 = L2 + L2
d2 = 52 + 52
d2 = 25 + 25
d2 = 50
d = √50
d = √2 x 52
d =5 √2
d = 7,071
Observação importante: geometricamente tem-se a diagonal do quadrado (lados 5cm) medindo 7cm (número inteiro) e algebricamente 7,07...(número irracional).
Efetuando cálculos com o Teorema de Pitágoras do quadrado maior de lados 7cm:
d2 = L2 + L2
d2 = 72 + 72
d2 = 49 + 49
d2 = 98
d = √98
d = √2 x 72
d = 7 √2
d = 9,899
Observação importante: geometricamente tem-se a diagonal do quadrado (lados 7cm) medindo 10cm (número inteiro) e algebricamente 9,89...(número irracional).
Efetuado-se os cálculos aritméticos das áreas do novo quadrado gerado do Triângulo Pitagórico 3-4-5:
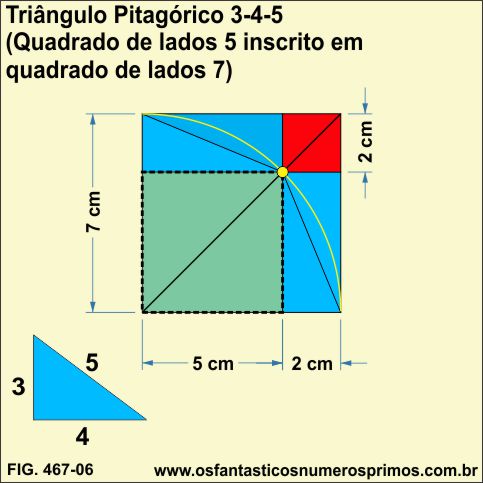
a) área do quadrado inscrito (verde)
5 x 5 = 25
b) áreas dos dois retângulos (azuis)
2 x 5 = 10
2 x 5 = 10
c) área do quadrado menor (vermelho)
2 x 2 = 4
A soma das áreas dos retângulos (azuis) e do quadrado menor (vermelho) não é igual a do quadrado inscrito (verde)
20 + 4 = 24
A área do quadrado inscrito difere em 1 unidade em relação as áreas dos retângulos com o quadrado menor.
A área do quadrado inscrito é mais que a metade do quadrado principal.
Os quadrados dinâmicos são sequências de quadrados obtidos a partir de um quadrado de lados unitários e que podem ser replicados proporcionalmente por meio do ponto médio dos seus lados, pelas suas diagonais ou pelos seus lados.
Veja matérias relacionadas, para mais informações!
Na construção de quadrados dinâmicos a partir do ponto médio dos lados do quadrado, conforme exemplo, o quadrado principal (vermelho) e a sua réplica (verde), vê-se que o quadrado (verde) é semelhante e tem a mesma área remanescente do quadrado vermelho (formado por triângulos retângulos isóceles).
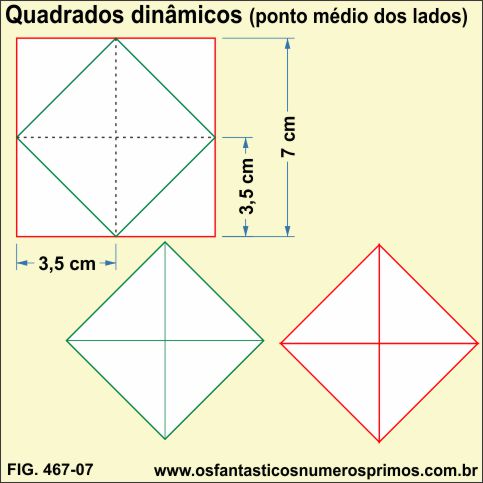
Efetuando-se os cálculos aritméticos:
a) área de 1 triângulo (vermelho)
(3,5 x 3,5) / 2 = 6,126
b) área de 4 triângulos (vermelhos)
4 x 6,125 = 24, 5
c) área de 1 triângulo (verde)
(3,5 x 3,5) / 2 = 6,126
d) área de 4 triângulos (verdes)
4 x 6,125 = 24, 5
A soma das áreas de todos os triângulos é igual a do quadrado principal (vermelho) que é 7 x 7 = 49cm2.
24,5 + 24,5 = 49
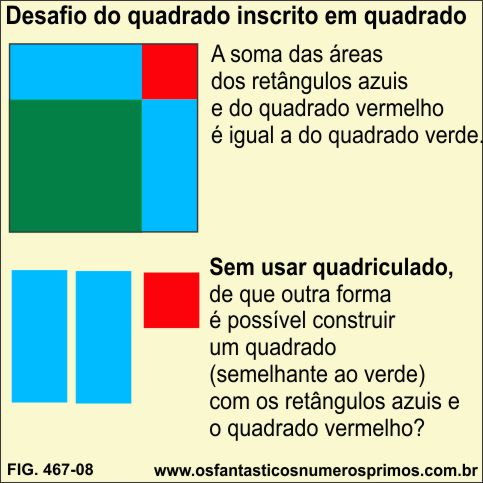
O WebSite Os Fantásticos Números Primos deixa o seguinte desafio geométrico a você, estimado, visitante.
Autor: Ricardo Silva - outubro/2023
[1]DANTE, Luiz Roberto Dante. Tudo é Matêmáica / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato