


O Teorema de Pitágoras apresenta o seguinte enunciado: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos e o que também é verdade: A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
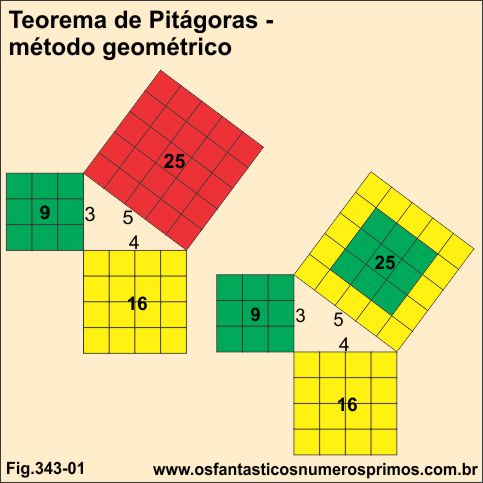
O teorema é facilmente comprovado, desenhando-se um triângulo retângulo e posteriormente quadrados em cada um dos seus lados.
Quadriculando as áreas dos quadrados e somando-se os quadradinhos das áreas dos catetos, o resultado é a mesma quantidade de quadradinhos da área do quadrado da hipotenusa.
Nesta demonstração do Teorema de Pitágoras, as áreas dos quadrados foram quadriculadas formando-se áreas quadradas menores cujos lados dos quadradinhos possuem a mesma medida.
As áreas dos quadrados dos catetos foram decompostas em quadradinhos menores e que posteriormente foram justapotas na área do quadrado da hipotenusa assim provando o Teorema de Pitágoras.
Esta é apenas umas das demonstrações do Teorema de Pitágoras, há outras centenas de demonstrações classificadas dependendo de suas caracteristicas comuns, tais como: algébricas, geométricas, decomposições de áreas, etc.
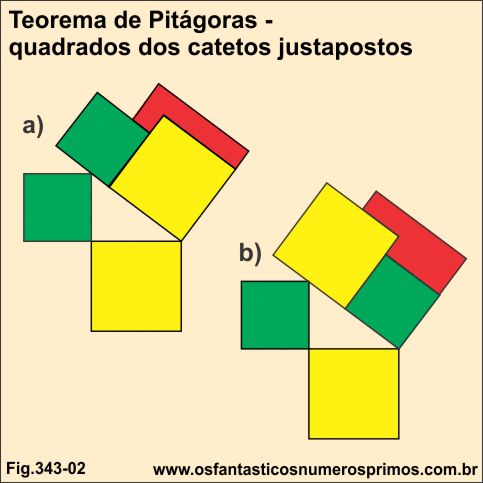
Sem decompor as áreas dos quadrados dos catetos em áreas menores é possível formar a área do quadrado da hipotenusa geometricamente?
Conforme os exemplos a) e b) da figura 343-02 não são possíveis de se formarem as áreas dos quadrados das hipotenusas justapondo-se os quadrados dos catetos.
A sequência de Fibonacci é formada repetindo-se o número 1 e posteriormente somando-se dois termos anteriores a partir do terceiro termo.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,...
A soma de termos consecutivos de Fibonacci ao quadrado apresentam uma outra interessante sequência numérica com a qual são possíveis de formarem figuras de quadrados e retângulos justapondo-as consecutivamente, formando-se retângulos cujos comprimentos e alturas são os próprios números consecutivos de Fibonacci.
1² + 1² = 2
1² + 1² + 2² = 6
1² + 1² + 2² + 3²= 15
1² + 1² + 2² + 3² + 5² = 40
1² + 1² + 2² + 3² + 5² + 8² = 104
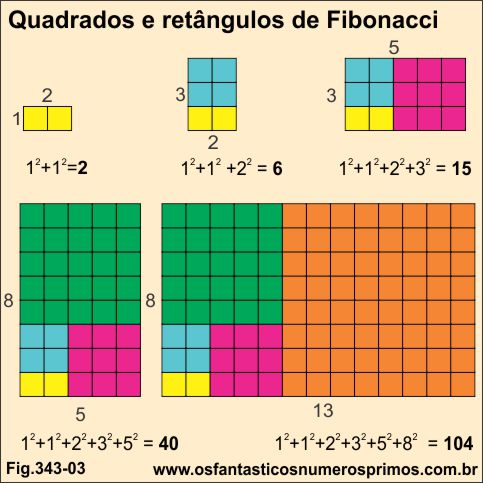
Fonte: CARVALHO, Maria Cecília Costa e Silva. Padrões numéricos e sequências: São Paulo, Moderna, 1997
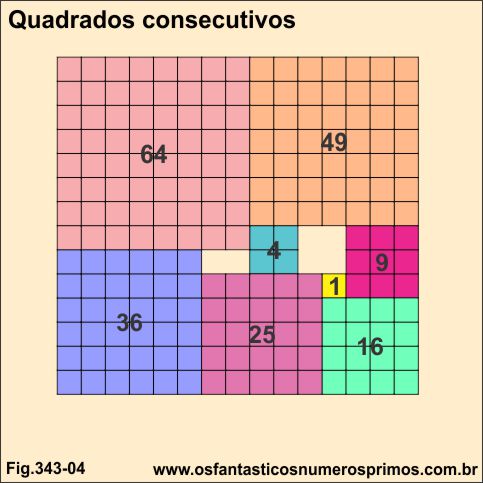
Com figuras de quadrados de lados 1, 2, 3, 4, 5, 6 7 e 8 cujas respectivas áreas formando quadrados: 1, 4, 9, 16, 25, 36, 49 e 64 quadriculados não são possíveis de se formar um quadrado maior, pois ficam faltando áreas a serem preenchidas.
No exemplo, há uma área de 4 quadradinhos e outras duas de 1 quadradinho faltantes.
Quadrados dinâmicos são construções geométricas de quadrados proporcionais.
No exemplo, um dos métodos de construções: a partir de um quadrado de lado unitário, podem ser obtidos duas séries de quadrados proporcionais em progressões geométricas: 1, 2, 4, 8, 16,... e outra: √2, 2√2, 4 √2, 8√2, 16√2,...
Veja matérias relacionadas abaixo, para conhecer outros métodos de construções.
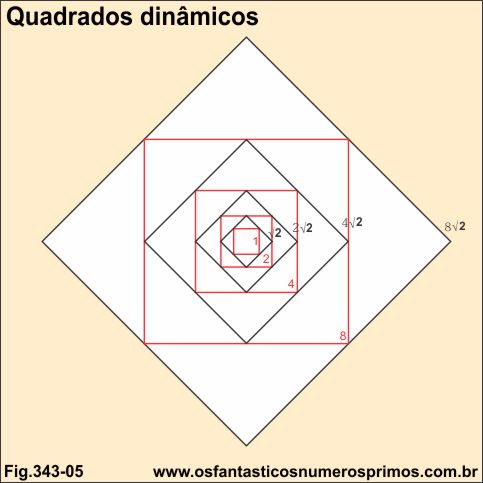
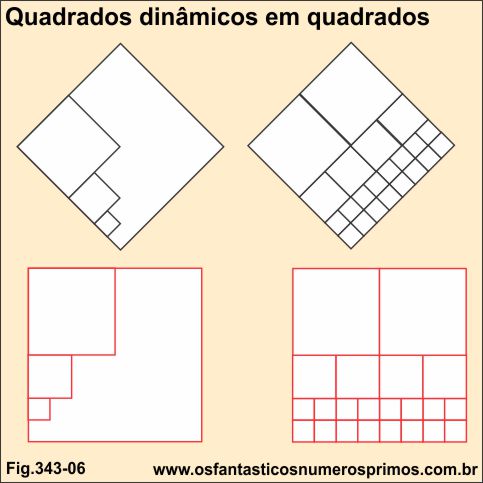
Tentando-se reconstruir um quadrado dinâmico com quadrados dinâmicos menores, necessariamente precisam ser os quadrados menores replicados para se poder formar a área de um quadrado maior.
A construção de quadrados formados por quadrados a seguir é creditada T. H. Willcocks, um estudante inglês.
A demonstração se encontra publicada no livro Matematics on Vacation, do ano de 1966, de autoria do estadunidense Joseph S. Madachy.
Interessante observar que nesta construção com 23 quadrados, há 6 quadrados cujos lados são medidas de quadrados perfeitos e os demais não.
1, 4, 9, 16, 64 e 81 - quadrados perfeitos.
3, 2, 5, 8, 14 18, 20, 29, 30, 31, 33, 35, 39, 43, 51, 55 e 56 - não quadrados perfeitos.
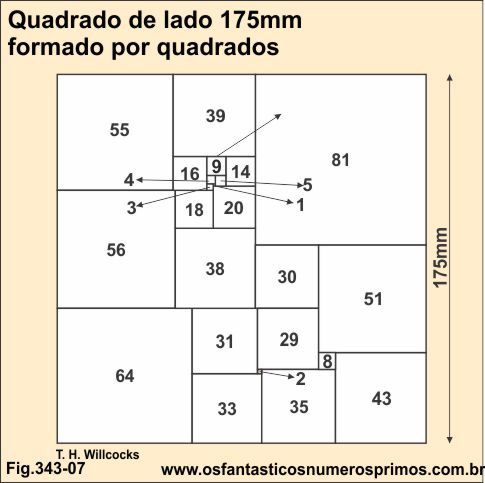
Fonte: Madachy, Joseph S. Matematics on Vacacion
Autor: Ricardo Silva - maio/2021
CARVALHO, Maria Cecília Costa e Silva. Padrões numéricos e sequências: São Paulo, Moderna, 1997
MADACHY, Joseph S. Matematics on Vacacion. EUA, Charles Scribner's Sons, 1966
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato