


Números Naturais é uma sequência numérica infinita na qual se encontra diversas outras sequências numéricas famosas, como: números ímpares, números pares, números figurados (triangulares, quadrados, pentagonais, etc.), potências, bem como, os fantásticos números primos.
Até o presente momento, ainda não se tem uma fórmula que gerem sequencialmente números primos.
O presente estudo demonstra regularidades numéricas nas somas de potências consecutivas, bem como, nas somas cujas quantidades de termos dessas potências são constantes.
Demonstra também que a Proposição 36, do IX livro, de Os Elementos de Euclides de Alexandria é válida para somas de potências consecutivas diferentes da base 2.
Somas de potências em que o resultado é um número primo e este multiplicado pela última parcela da soma geram produtos cujas quantidades de divisores são metade potências de um numero e a outra metade múltiplos de um número primo.
A soma de números pares têm como resultados números pares.
0 + 2 = 2
2 + 2 = 4
4 + 2 = 6
As somas de 2 números naturais consecutivos, sendo um ímpar e outro par ou vice-versa, têm como resultados números ímpares distintos e, entre eles, números primos.
1 + 2 = 3 (primo)
2 + 3 = 5 (primo)
3 + 4 = 7 (primo)
4 + 5 = 9
5 + 6 = 11 (primo)
6 + 7 = 13 (primo)
7 + 8 = 15
A soma de números naturais consecutivos têm como resultados números figurados triangulares.
Números Figurados são números que por meio de arranjos de pontos podemos formar figuras geométricas.
1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
Potências de um número natural são produtos obtidos da multiplicação de um número natural por ele mesmo, tantas vezes que se queira.
Partindo-se do 1 (um) e dobrando os valores, obtêm-se potências de base 2.
(1, 2, 4, 8, 16, 32, 64, 128, 256, 512,...)
20 = 1
21 = 2
22 = 2 x 2 = 4
23 = 2 x 2 x 2 = 8
24 = 2 x 2 x 2 x 2 = 16
25 = 2 x 2 x 2 x 2 x 2 = 32
As potências de base 2 são produtos exclusivos da base 2, de forma que, de qualquer potência de base 2, dividindo-se por 2 sequencialmente, chega-se a unidade (número 1).
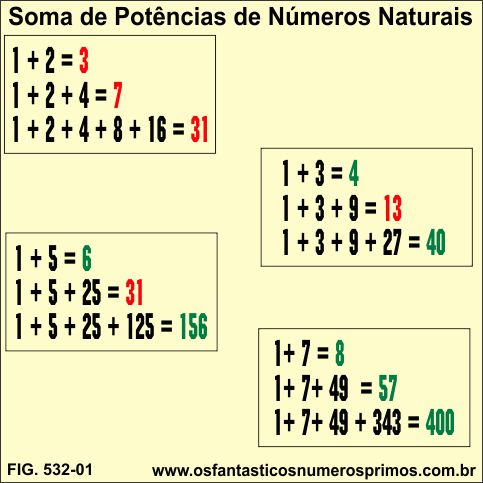
As somas de potências de base 2 consecutivas têm como resultados números ímpares e, entre eles, números primos.
Somas de potências de base 2 consecutivas também são denominadas de Números de Mersenne / Números Quase-Pontências de Base 2, por apresentarem 1 unidade de diferença de uma potência de base 2
1 + 2 = 3 (primo)
1 + 2 + 4 = 7 (primo)
1 + 2 + 4 + 8 = 15
1 + 2 + 4 + 8 + 16 = 31 (primo)
1 + 2 + 4 + 8 + 16 + 32 = 63
1 + 2 + 4 + 8 + 16 + 32 + 64 = 127 (primo)
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 = 511
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 = 1.023
Observação importante: nenhuma soma de potências de base 2 é divisível por sua base, isto é, pelo número 2.
Soma de 2 potências consecutivas de base 2
As somas de 2 potências de base 2 consecutivas têm como resultados múltiplos de 3.
1 + 2 = 3, o mesmo que 1 x 3 = 3
2 + 4 = 6, o mesmo que 2 x 3 = 6
Observação: 2 (potência) x 3 primo = 6
D(6): {1, 2, 3, 6}
4 são os divisores de 6.
2 divisores são potências de base 2.
2 divisores são múltiplos do número primo 3.
Observações importantíssimas:
a) na demonstração deste exemplo, deduz-se um novo método de se obterem divisores de determinado número composto que é produto de uma potência por um número primo por meio de multiplicação.
b) 6 é um número perfeito e possui divisores cujas quantidade são metade potências de base 2 e a outra metade múltiplos do número primo 3.
Soma de 3 potências consecutivas de base 2
As somas de 3 potências de base 2 consecutivas têm como resultados múltiplos de 7.
1 + 2 + 4 = 7, o mesmo que 1 x 7 = 7
2 + 4 + 8 = 14, o mesmo que 2 x 7 = 14
4 + 8 + 16 = 28, o mesmo que 4 x 7 = 28
Observação: 4 (potência) x 7 primo = 28
D(28): {1, 2, 4, 7, 14, 28}
6 são os divisores de 28.
3 divisores são potências de base 2.
3 divisores são múltiplos do primo 7.
Observações importantíssimas:
a) na demonstração deste exemplo, deduz-se um novo método de se obterem divisores de determinado número composto que é produto de uma potência por um número primo por meio de multiplicação.
b) 28 é um número perfeito e possui divisores cujas quantidade são metade potências de base 2 e a outra metade múltiplos do número primo 7.
Soma de 4 potências consecutivas de base 2
As somas de 4 potências de base 2 consecutivas têm como resultados múltiplos de 15.
1 + 2 + 4 + 8 = 15, o mesmo que 1 x 15 = 15
2 + 4 + 8 + 16 = 30, o mesmo que 2 x 15 = 30
4 + 8 + 16 + 32 = 60, o mesmo que 4 x 15 = 60
Número perfeito é um número cuja soma de seus divisores próprios, exceto esse número, têm como resultado esse número.
Euclides de Alexandria, em sua obra, Os Elementos, Livro IX, proprosição 36, já havia demonstrado que a partir da unidade (número 1), duplicando e somando consecutivamente os termos, até que se encontre um número primo, e este primo multiplicado pela última parcela da soma, então o produto é um número perfeito.
Fórmula de Euclides em notação moderna é:
| 2^n-1 [ ( 2^n ) - 1 ] |
Euclides estava se referindo às somas de potências de base 2 consecutivas:
a) 1 + 2 = 3 (número primo)
3 x 2 = 6
6 é um número perfeito
b) 1 + 2 + 4 = 7 (número primo)
7 x 4 = 28
28 é um número perfeito
c) 1 + 2 + 4 + 8 + 16 = 31 (número primo)
31 x 16 = 496
496 é um número perfeito
No livro digital Números Perfeitos e Sequências numéricas é apresentado a seguinte propriedade:
"Os divisores dos números perfeitos apresentam regularidades em
suas quantidades; metade são potências de base 2; e a outra metade o
dobro, do dobro, do dobro, ... de números primos."
Os dois termos centrais dos divisores são fatores que determinam um número perfeito, isto é, o produto de uma potência de base 2 por um número primo."
| Números Perfeitos | |
| e quantidades de divisores | |
| número perfeito 6 | |
| 2 divisores | 2 divisores |
| 1, 2, | 3, 6 |
| número perfeito 28 | |
| 3 divisores | 3 divisores |
| 1, 2, 4, | 7, 14, 28 |
| número perfeito 496 | |
| 5 divisores | 5 divisores |
| 1, 2, 4, 8, 16, | 31, 62, 124, 248, 496 |
| número perfeito 8128 | |
| 7 divisores | 7 divisores |
| 1, 2, 4, 8, 16, 32, 64 | 127, 254, 508, 1016, 2032, 4064, 8128 |
| www.osfantasticosnumerosprimos.com.br | |
Método de Euclides
O Método de Euclides, referenciado acima, também pode ser aplicado à somas de potências de outras bases.
A soma de potências consecutivas de um número natural sendo um número primo e, este múltiplicado pela última parcela da soma, tem como resultado um produto cuja quantidade de divisores são formadas por 2 conjuntos de divisores: uma metade por potências desse número natural e a outra metade por múltiplos desse número primo.
Para mais informações veja:
011-estudos-531-somas-de-potencias-e-numeros-primos
Soma de potências de base 3 consecutivas
Partindo-se do 1 (um) e triplicando os valores, obtêm-se potências de base 3.
(1, 3, 9, 27, 81, 243, 729, 2.187, 6561, 19683, ...)
A soma de potências consecutivas de base 3 têm como resultados números pares e ímpares e, entre eles, números primos.
1 + 3 = 4 (composto)
1 + 3 + 9 = 13 (primo)
1 + 3 + 9 + 27 = 40 (composto)
1 + 3 + 9 + 27 + 81 = 121 (quadrado)
1 + 3 + 9 + 27 + 81 + 243 = 364 (composto)
1 + 3 + 9 + 27 + 81 + 243 + 729 = 1.093 (primo)
1 + 3 + 9 + 27 + 81 + 243 + 729 + 2.187 = 3.280 (composto)
1 + 3 + 9 + 27 + 81 + 243 + 729 + 2.187 + 6.561 = 9.841 (composto)
1 + 3 + 9 + 27 + 81 + 243 + 729 + 2.187 + 6.561 + 19683 + 59049 + 177147 + 531441 = 797161 (primo)
As potências de base 3 são produtos exclusivos da base 3, de forma que, de qualquer potência de base 3, dividindo-se por 3 sequencialmente, chega-se a unidade (número 1).
Observação importante: nenhuma soma de potências de base 3 é divisível por sua base, isto é, pelo número 3.
Soma de 2 potências consecutivas de base 3
As somas de 2 potências de base 3 consecutivas têm como resultados múltiplos de 4.
1 + 3 = 4, o mesmo que 1 x 4 = 4
3 + 9 = 12, o mesmo que 3 x 4 = 12
9 + 27 = 36, o mesmo que 9 x 4 = 36
Soma de 3 potências consecutivas de base 3
As somas de 3 potências de base 3 consecutivas têm como resultados múltiplos de 13.
1 + 3 + 9 = 13, o mesmo que 1 x 13 = 13
3 + 9 + 27 = 39, o mesmo que 3 x 13 = 39
9 + 27 + 81 = 117, o mesmo que 9 x 13 = 117
Observação: 9 (potência) x 13 primo = 117
D(117): {1, 3, 9, 13, 39, 117}
6 são os divisores de 117.
3 divisores são potências de base 3.
3 divisores são múltiplos do primo 13.
Observações importantíssimas:
a) na demonstração deste exemplo, deduz-se um novo método de se obterem divisores de determinado número composto que é produto de uma potência por um número primo por meio de multiplicação.
b) 117 não é um número perfeito, mas possui quantidades e características dos divisores semelhantes aos de números perfeitos.
Soma de 4 potências consecutivas de base 3
As somas de 4 potências de base 3 consecutivas têm como resultados múltiplos de 40.
1 + 3 + 9 + 27 = 40, o mesmo que 1 x 40 = 40
3 + 9 + 27 + 81 = 120, o mesmo que 3 x 40 = 120
9 + 27 + 81 + 243 = 360, o mesmo que 9 x 40 = 360
Autor: Ricardo Silva e Ari Costa - dezembro/2024
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato